HDU

线上题目：

推箱子

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 4927    Accepted Submission(s): 1377

Problem Description

推 箱子是一个很经典的游戏.今天我们来玩一个简单版本.在一个M*N的房间里有一个箱子和一个搬运工,搬运工的工作就是把箱子推到指定的位置,注意,搬运工 只能推箱子而不能拉箱子,因此如果箱子被推到一个角上(如图2)那么箱子就不能再被移动了,如果箱子被推到一面墙上,那么箱子只能沿着墙移动.

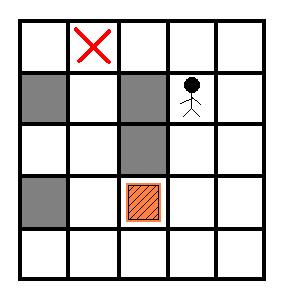
现在给定房间的结构,箱子的位置,搬运工的位置和箱子要被推去的位置,请你计算出搬运工至少要推动箱子多少格.

 

Input

输 入数据的第一行是一个整数T(1<=T<=20),代表测试数据的数量.然后是T组测试数据,每组测试数据的第一行是两个正整数M,N(2& lt;=M,N<=7),代表房间的大小,然后是一个M行N列的矩阵,代表房间的布局,其中0代表空的地板,1代表墙,2代表箱子的起始位置,3代 表箱子要被推去的位置,4代表搬运工的起始位置.

 

Output

对于每组测试数据,输出搬运工最少需要推动箱子多少格才能帮箱子推到指定位置,如果不能推到指定位置则输出-1.

 

Sample Input

1

5 5

0 3 0 0 0

1 0 1 4 0

0 0 1 0 0

1 0 2 0 0

0 0 0 0 0

 

Sample Output

4

 

　　中文题意不解释，做法是BFS,但是和普通的BFS有点不一样,先说一下我的思路。

　　对于一副地图，先保存下人和箱子以及终点，然后将可以走和不可以走的点都区分好。然后我们只需要记录的状态是人和箱子的位置以及步数，我们需要判重人和箱子的位子所表示的状态是否已经出现过了，当箱子到达了目标地点的时候我们就返回步数，否则就返回-1,但是这里我们需要保证输出的步数一定是最小的，我们需要注意的是如果只是用队列来实现的话，不一定能保证到达的时候一定是最近，因为中途会遇到墙壁什么的，同时人去找箱子的过程也需要考虑会不会影响，所以这里我们需要使用的是优先队列，优先级是当前所走的步数，步数小的优先，看起来有点像启发式搜索= =，但是不算很明显。

 

上代码：

 

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#include <vector>
#include <set>
#define INF (1<<30)
#define MAX 10
using namespace std;

typedef struct state{
    int by,bx;
    int ry,rx;
    int step;

    bool operator < (const state& o)const{
        return step>o.step;
    }

    bool operator == (const state& o)const{
        return (by==o.by && bx==o.bx && ry==o.ry && rx==o.rx);
    }

}state;

int cy[]={0,1,0,-1};
int cx[]={-1,0,1,0};
int minn;
int n,m;
int mp[MAX][MAX];
int ey,ex;
vector<state> vv;
priority_queue<state> q;
int isok(state v){
    if(0<=v.ry && v.ry<n && 0<=v.rx && v.rx<m && mp[v.ry][v.rx]!=1){
        if(v.ry ==v.by && v.rx == v.bx) return -1;
        return 1;
    }
    return 0;
}

bool isexist(state v){
    for(unsigned int i=0;i<vv.size();i++) if(vv[i] == v) return 1;
    vv.push_back(v);
    return 0;
}

bool canPush(state v,int dir){
    v.by+=cy[dir];    v.bx+=cx[dir];
    if(0<=v.by && v.by<n && 0<=v.bx && v.bx<m && mp[v.by][v.bx]==0) return 1;
    return 0;
}

int bfs(){
    state u,v;
    while(!q.empty()) q.pop();
    vv.clear();
    for(int i=0;i<n;i++) for(int j=0;j<m;j++)
        if(mp[i][j]== 2){
            u.by = i; u.bx = j; mp[i][j] = 0;
        }else if(mp[i][j] == 3){
            ey = i; ex = j;     mp[i][j] = 0;
        }else if(mp[i][j] == 4){
            u.ry = i; u.rx= j;  mp[i][j] = 0;
        }
    u.step = 0;
    q.push(u);
    int co = 0;
    while(!q.empty()){
        u = q.top();
        q.pop();
        co++;
        for(int i=0;i<4;i++){
            v = u;
            v.ry+=cy[i];    v.rx+=cx[i];
            int f = isok(v);
            if(f == 0) continue;
            else if(f == 1 && isexist(v)) continue;
            else if(f == -1){
                 if(!canPush(v,i)) continue;
                 v.by+=cy[i];   v.bx+=cx[i];
                 v.step++;
                 if(v.by == ey && v.bx == ex){ return v.step ;}
                 if(isexist(v)) continue;
            }
            q.push(v);
        }
    }
    return -1;
}

int main()
{
    int t;
    //freopen("ans.txt","r",stdin);
    scanf("%d",&t);
    while(t--){
        scanf("%d %d",&n,&m);
        for(int i=0;i<n;i++) for(int j=0;j<m;j++) scanf("%d",&mp[i][j]);
        int ans = bfs();
        printf("%d
",ans);
    }
    return 0;
}