1.六轴机械手臂一般使用6个量来表示其空间点（位置与姿态）
表示空间姿态的有三种方式：RPY角(roll pitch yaw)和欧拉角(euler angles),旋转矩阵
RPY:先绕Z轴旋转，再绕Y轴旋转，最后是绕X轴旋转。
欧拉角：先绕Z轴旋转，再绕Y轴旋转，最后再绕Z轴旋转
旋转矩阵:先绕X轴旋转，再绕Y轴旋转，最后再绕Z轴旋转。
（1）.staubli是使用旋转矩阵
（2）.ABB使用欧拉角
2.姿态等效旋转轴的计算
百度文库中有个详细的介绍 http://wenku.baidu.com/view/d2b7345a804d2b160b4ec0a0.html
3.trsf介绍
史陶比尔的Trsf可以表示为一个在三维空间中任意一点的位置与姿态。一共六个量。
trsf={x,y,z,rx,ry,rz} 其中rx,ry,rz的取值范围是（-180～180）
x表示在X轴方向上的平移
y表示在Y轴方向上的平移
z表示在Z轴方向上的平移
(r是rotate， 表示旋转的意思)
rx表示在X轴方向的旋转
ry表示在Y轴方向的旋转
rz表示在Z轴方向的旋转
顺序：先平移x,再平移y,然后z,接着旋转rx,再旋转ry,最后旋转rz
4 trsf与四阶矩阵的相互转化
trsf每一个量都可以表示为一个四阶矩阵。
trsf=matrix(x)*matrix(y)*matrix(z)*matrix(rx)*matrix(ry)*matrix(rz)
其中 =trsf.rx; =trsf.ry; =trsf.rz; x=trsf.x/1000,y=trsf.y/1000,z=trsf.z/1000
5.空间位置矩阵一般都是表示为
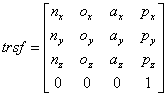
n,o,a,p 是三维的列向量 ， 其中 n,o,a,p是相互正交的单位向量 ， 表示了该坐标系相对于参考坐标系的姿态， p 向量表示了该坐标系原点相对于参考坐标系的位置。
注： n 向量表示了该坐标系的 X 轴方向， o 向量表示了该坐标系的 Y 轴方向， a 向量表示了该坐标系的 Z 轴方向
6.转换矩阵与trsf之间的关系是：
从矩阵转换为trsf时，一般至少有两解
由于范围均在（-180～180）内，tan和sin可以获得两个解。
比如（30，120，-45）（-150，60，135）
在某些模拟器其中，会进行强制转换。rx强制在（-90～90）之间。
但是在程序中是可以赋值，运动的。
7.trsf的逆运算
trsf的逆就是其矩阵的逆 matrix(x)*matrx(y)*matrix(z)*matrix(rx)*matrix(ry)*matrix(rz)的逆，那么就是六个逆矩阵倒乘。
matrix(rz)，matrix(ry),matrix(rx),matrtix(z),matrix(y),matrix(x)的逆矩阵分别是
其逆阵就是上面六个式子相乘。
*
那么为
根据旋转矩阵就可以得到逆阵的x,y,z,rx,ry,rz