1.任务描述
1.1 概述
独立完成一个3到5个运算符的四则运算练习的软件,编程语言不限。
1.2 基本要求
程序可接收一个输入参数n,然后随机产生n道加减乘除(分别使用符号+-*÷来表示)练习题,每个数字在 0 和 100 之间,运算符在3个到5个之间。
每个练习题至少要包含2种运算符。同时,由于小学生没有分数与负数的概念,你所出的练习题在运算过程中不得出现负数与非整数,比如不能出 3÷5+2=2.6,2-5+10=7等算式。
练习题生成好后,将你的学号与生成的n道练习题及其对应的正确答案输出到文件“result.txt”中,不要输出额外信息,文件目录与程序目录一致。
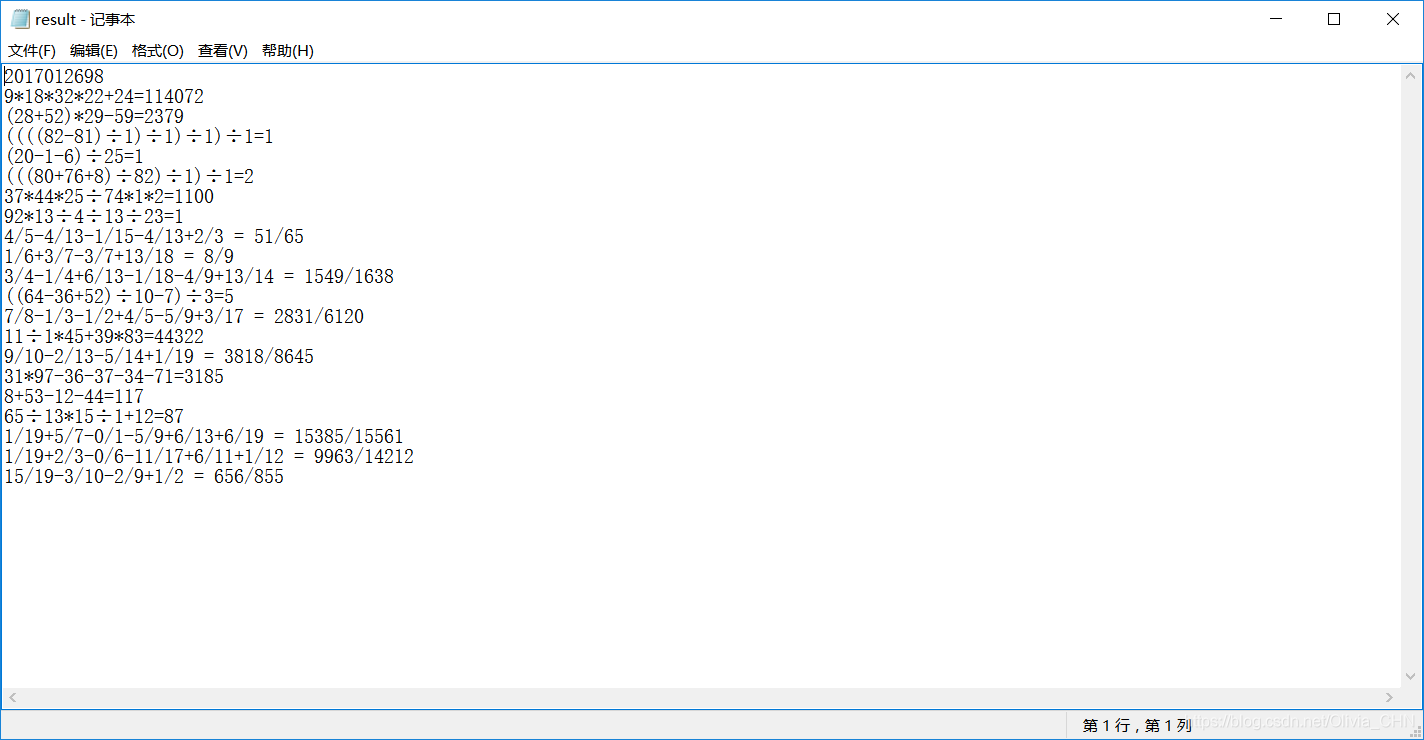
当程序接收的参数为4时,以下为一个输出文件示例。
1.3 附加功能
支持有括号的运算式,包括出题与求解正确答案。注意,算式中存在的括号数必须大于2对,且不得超过运算符的个数。
扩展程序功能支持真分数的出题与运算(只需要涵盖加减法即可),例如:1/6 + 1/8 + 2/3= 23/24。注意在实现本功能时,需支持运算时分数的自动化简,比如 1/2+1/6=2/3,而非4/6,且计算过程中与结果都须为真分数。
2.项目地址
github地址:https://github.com/Chenhn110/Test
Coding.net地址:https://dev.tencent.com/u/Chenhn/p/Test/git/tree/master/Calculate
3.项目部分源代码
1 import java.util.Random; 2 3 4 public class Calculate { 5 public static void Integer(){ 6 String arith1 = null;//运算式 7 char[]optCom = {'+','-','*','÷'}; //加减乘除操作集 8 Random random = new Random(); 9 int optIdx = random.nextInt(4); 10 int sum1 = 0;//每步运算结果 11 int optNum = random.nextInt(3) + 3; //3-5个运算符 12 int a = random.nextInt(100);//随机生成0-100内的整数a 13 int b = random.nextInt(100);//随机生成0-100内的整数b 14 if(optCom[optIdx] == '+') sum1 = a + b; 15 if(optCom[optIdx] == '*') sum1 = a * b; 16 if(optCom[optIdx] == '-'){//若a-b为负数,则重新随机产生a b 17 while(a-b < 0) 18 { 19 a = random.nextInt(100); 20 b = random.nextInt(100); 21 } 22 sum1 = a - b; 23 } 24 if(optCom[optIdx] == '÷'){//若a÷b不能整除,则重新随机产生a b 25 if (b == 0) 26 b = random.nextInt(100); 27 while (a%b != 0) { 28 a = random.nextInt(100); 29 b = random.nextInt(100); 30 } 31 sum1 = a/b; 32 } 33 arith1 = a + "" + optCom[optIdx] + "" + b;//将算式更新 34 35 for(int j = 1; j < optNum; j++){//随机生成余下的运算符 36 int optIdx1 = random.nextInt(4);//随机生成下一个运算符号 37 int c = random.nextInt(100);//随机生成0-100内的整数c 38 if(optCom[optIdx1] == '+'){ 39 sum1 += c; 40 arith1 = arith1 + "" + optCom[optIdx1] + "" + c; 41 } 42 if(optCom[optIdx1] == '-'){ 43 while(sum1-c<0) 44 { 45 c=random.nextInt(100); 46 } 47 sum1 += c; 48 arith1 = arith1 + "" + optCom[optIdx1] + "" + c; 49 } 50 if(optCom[optIdx1] == '*'){//若下一个运算符号为乘号,判断前后两个运算符的优先级 51 if(optCom[optIdx] == '+' || optCom[optIdx] == '-') 52 { 53 arith1 = "(" + arith1 + ")" + optCom[optIdx1] + c; 54 } 55 else 56 { 57 arith1 = arith1 + "" + optCom[optIdx1] + "" + c; 58 } 59 sum1 = sum1*c; 60 } 61 if(optCom[optIdx1] == '÷'){//若下一个运算符号为除号,判断前后两个运算符的优先级 62 while (c == 0 || sum1%c != 0) { 63 c=random.nextInt(100); 64 } 65 if(optCom[optIdx] == '+' || optCom[optIdx] == '-') 66 { 67 arith1= "(" + arith1 + ")" + optCom[optIdx1] + c; 68 } 69 else 70 { 71 arith1 = arith1 + "" + optCom[optIdx1] + "" + c; 72 } 73 sum1 = sum1/c; 74 } 75 // optIdx = optIdx1;//更新运算符 76 } 77 System.out.println(arith1 + "=" + sum1);//输出运算式及结果 78 } 79 public static void Fraction(){ 80 String arith2 = null;//运算式 81 //String sum2 = null; 82 char[]optSim = {'+','-'}; //分数加减操作集 83 Random random = new Random(); 84 int mole = 0; 85 int deno = 0; //初始化分子分母 86 int optNum = random.nextInt(3) + 3; //3-5个运算符 87 int mole1 = random.nextInt(20)+1;//随机生成分子1 88 int deno1 = random.nextInt(20)+1;//随机生成分母1 89 if (mole1 != 0 && deno1 != 0) { 90 if (mole1 > deno1) {// 如果分子大于分母,也就是不是真分数时,交换分子分母,使其变成真分数 91 int temp = mole1; 92 mole1 = deno1; 93 deno1 = temp; 94 } 95 if (mole1 == deno1) {// 如果分子刚好等于分母,重新生成分子 96 mole1 = random.nextInt(20); 97 } 98 int gcd1 = gcd(mole1, deno1);// 求分子分母最大公因数,保证分数形式最简 99 deno1 = deno1 / gcd1;// 化简 100 mole1 = mole1 / gcd1;// 化简 101 } 102 arith2 = mole1 + "/" + deno1;// 存储题目 103 for (int k = 0; k < optNum; k++) {// 小于运算符数量时不断产生分数,不断计算 104 int deno2 = random.nextInt(20);// 生成分母 105 int mole2 = random.nextInt(20);// 生成分子 106 if (mole2 != 0 && deno2 != 0) { 107 if (mole2 > deno2) {// 避免不是真分数 108 int temp = mole2; 109 mole2 = deno2; 110 deno2 = temp; 111 112 } 113 if (mole2 == deno2) {// 如果分子等于分母,重新生成分子 114 mole2 = random.nextInt(20); 115 } 116 int gcd2 = gcd(mole2, deno2);// 化简分式,使其最简 117 deno2 = deno2 / gcd2; 118 mole2 = mole2 / gcd2; 119 } 120 int idx = random.nextInt(2);//随机生成运算符下标 121 if (optSim[idx] == '+') {// 如果是加号,实现分数加法 122 if (deno1 == deno2) {// 如果两个分母相同,直接将分子相加 123 mole = mole1 + mole2; 124 } else {// 通分,相加 125 deno = deno1 * deno2; 126 mole = mole1 * deno2 + mole2 * deno1; 127 } 128 if (mole > deno) {// 如果运算结果不是真分数 129 k--;// 计数的u减一,也就是重新生成重新计算 130 } else {// 在给定范围内的话,通分运算结果 131 int gcd = gcd(mole, deno); 132 deno = deno / gcd; 133 mole = mole / gcd; 134 arith2 = arith2 + optSim[idx] + mole2 + "/" + deno2; 135 deno1 = deno;// 储存通分结果 136 mole1 = mole; 137 } 138 } else {// 如果是减号,实现减法操作 139 if (deno1 == deno2) {// 分母相同直接分子相减 140 mole = mole1 - mole2; 141 } else {// 其他情况,先通分再相减 142 deno = deno1 * deno2; 143 mole = mole1 * deno2 - mole2 * deno1; 144 } 145 if (mole < 0) {// 如果导致结果小于0了,就重新生成 146 k--; 147 } else {// 通分结果化简 148 int gcd = gcd(mole, deno); 149 deno = deno / gcd; 150 mole = mole / gcd; 151 arith2 = arith2 + optSim[idx] + mole2 + "/" + deno2; 152 deno1 = deno;// 储存通分结果 153 mole1 = mole; 154 } 155 } 156 } 157 System.out.println(arith2 + " = " + mole + "/" + deno);// 输出题目和答案 158 159 } 160 161 //最大公因数,每次代入,显然有a<b 162 public static int gcd(int a, int b){ 163 while(a!=0) 164 return gcd(b % a, a); 165 return b; 166 } 167 168 public static void QuesFunc(int n) {// 实现产生n个混合四则运算的方法 169 Random random = new Random(); 170 for (int i = 0; i < n; i++) { 171 int flag = random.nextInt(4); //随机生成整数四则运算或真分数加减运算 172 if (flag == 0 || flag == 2) {//0生成整数四则运算 173 Integer(); 174 } else {//执行真分数加减运算 175 Fraction(); 176 } 177 } 178 } 179 }
4. 生成result.txt文件
5.PSP (个人软件开发流程)
