- 什么是数据结构?什么是算法
- 广义
- 数据结构:一组数据的存储结构
- 算法:操作数据的一组方法
- 例子:图书馆对书籍的分门别类存储=数据结构,查找一本书的方法=算法
- 狭义
- 著名的数据结构和算法:队列,栈,堆,二分查找,动态规划
- 重点:复杂度分析
- 10个常用的数据结构:数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie树
- 10个常用的算法:递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
- 方法:边学边练,适度刷题
- 打怪升级学习法:设定目标,达到目标
- 沉淀法:书读百遍其义自见
- 广义
- 复杂度分析
- 数据结构和算法本身解决的问题是"快"和“省”的问题
- 为什么需要复杂度分析?
- 测试结果非常依赖测试环境
- 测试结果受数据规模的影响很大
- 时间复杂度
- 大O复杂度表示法:所有代码的执行时间与每行代码的执行次数成正比
- 只关注循环次数最多的一段代码
- 加法法则:总复杂度等于量级最大的那段代码的复杂度
- 乘法法则:嵌套代码复杂度等于嵌套内外代码复杂度的乘积
- 常见时间复杂度
- 多项式量级
- 常量阶O(1):代码的执行时间不随n的增大而增长
- 对数阶O(logn):i=1;while (i <= n) {i = i * 2;}----计算循环执行次数最多的行的时间复杂度
- 线性对数阶O(nlogn):循环N次的对数阶
- 线性阶O(n):循环N次
- 平方阶O(n2) 立方阶O(n3),K次方阶O(nk)
- 非多项式量级:非常低效的算法
- 指数阶O(2n)
- 阶乘阶O(n!)
- 多项式量级
- 大O复杂度表示法:所有代码的执行时间与每行代码的执行次数成正比
- 空间复杂度:渐进空间复杂度,表示算法的存储空间和数据规模的增长关系
- 同时间复杂度,只需要算量级最大的空间存储
- 最好情况时间复杂度:理想情况的时间复杂度
- 最坏情况时间复杂度:最糟糕的情况下的时间复杂度
- 平均情况时间复杂度:所有出现的情况累加除以可能性出现的情况,加权平均复杂度,期望时间复杂度
- 均摊时间复杂度:把最坏的情况的时间复杂度均摊到所有耗时少的情况下---使用很少
- 数组
- 数组为什么从0开始编号?
- 下标应该定义为偏移,下标其实是为了确定与首地址的偏移位置
- C语言一开始用,后面的语言继承了这一点
- 线性表:数据排成像一条线一样的结构
- 连续的内存空间和相同数据类型:可以通过地址随机访问数组中的某个元素
- JVM清楚垃圾回收:标记已经删除的位置,当没有更多的存储空间的时候在执行删除操作
- 垃圾桶。生活中,我们扔进屋里垃圾桶的垃圾,并没有消失,只是被 '' 标记 '' 成了垃圾,只有垃圾桶塞满时,才会清理垃圾桶。再次存放垃圾
- 数组为什么从0开始编号?
- 链表
- 链表和数组的区别
- 数组需要连续的内存空间,链表不需要连续的存储空间
- 插入删除:数组O(n),链表O(1)
- 随机访问:数组O(1),链表O(n)
- 数组利于CPU的缓存机制,但是固定内存空间
- 链表可以动态扩容,但是没法有效的预读,对CPU的缓存不友好
- 单链表
- 头节点:第一个节点
- 尾节点:最后一个节点,指向Null
- 插入和删除,不需要为了保证连续而搬移节点,O(1)
- 随机查找,没有连续的存储,没有公式,只能一个一个往下数,O(n)
- 每个节点:值,后继指针
- 循环链表
- 特殊的单链表,唯一的区别是尾节点指向头节点
- 双向链表
- 每个节点:前驱指针,值,后继指针
- 删除操作
- 删除值等于某个定值的节点:需要遍历查找O(n)
- 删除给定指针指向的节点:需要删除前驱节点,还是得遍历O(n)
- 插入操作也同理
- 随机查找也比单链表更加高效
- 空间换时间的设计思想:缓存
- 代码的书写
- 技巧一:理解指针或引用的含义
- 将某个变量赋值给指针,实际上这个变量的地址赋值给指针
- 技巧二:警惕指针丢失和内存泄露
- 技巧三:利用哨兵简化实现难度
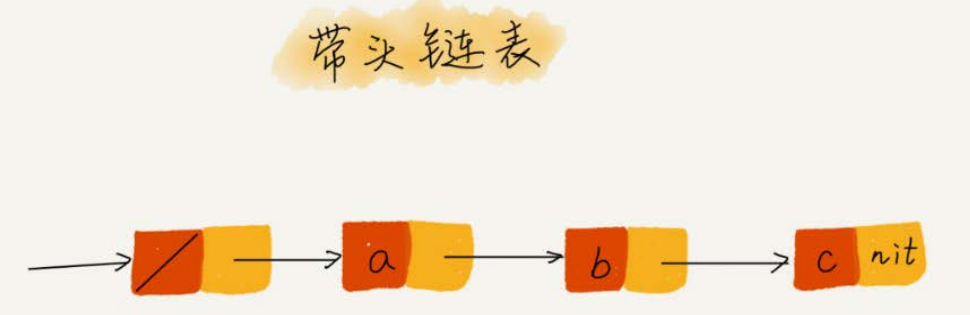
- 哨兵:head指针一直指向哨兵节点,哨兵节点不存储数据
- 技巧四:重点留意边界条件的处理
- 如果链表为空时,代码是否能正常工作?
- 如果链表只包含一个结点时,代码是否能正常工作?
- 如果链表只包含两个结点时,代码是否能正常工作?
- 代码逻辑在处理头结点和尾结点的时候,是否能正常工作?
- 技巧五:举例画图,辅助思考
- 技巧六:多写多练,没有捷径
- 常见的操作
- 单链表反转
- 链表中环的检测
- 两个有序的链表合并
- 删除链表倒数第n个结点
- 求链表的中间结点
- 技巧一:理解指针或引用的含义
- 链表和数组的区别
- 栈
- 如何实现浏览器的前进和后退功能?
- 我们使用两个栈, X 和 Y ,我们把首次浏览的页面依次压入栈 X ,当点击后退按钮时,再依次从栈 X 中出栈,并将出栈的数据依次放入栈 Y 。当我们点击前进按钮时,我们依次从栈 Y 中取出数据,放入栈 X 中。当栈 X 中没有数据时,那就说明没有页面可以继续后退浏览了。当栈 Y 中没有数据,那就说明没有页面可以点击前进按钮浏览了。
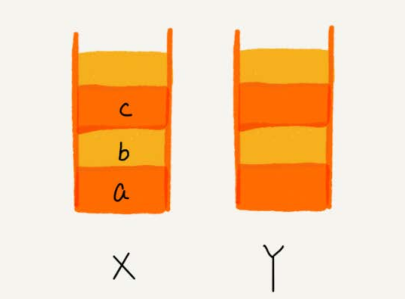
- 理解:一摞叠在一起的盘子,只能后进先出,先进后出
- 操作
- 只能在一端插入和删除-----入栈和出栈 O(1)
- 栈在函数调用中的应用
- 操作系统给每个线程分配了一块独立的内存空间,这块内存被组织成 “ 栈 ” 这种结构 , 用来存储函数调用时的临时变量。每进入一个函数,就会将临时变量作为一个栈帧入栈,当被调用函数执行完成,返回之后,将这个函数对应的栈帧出栈
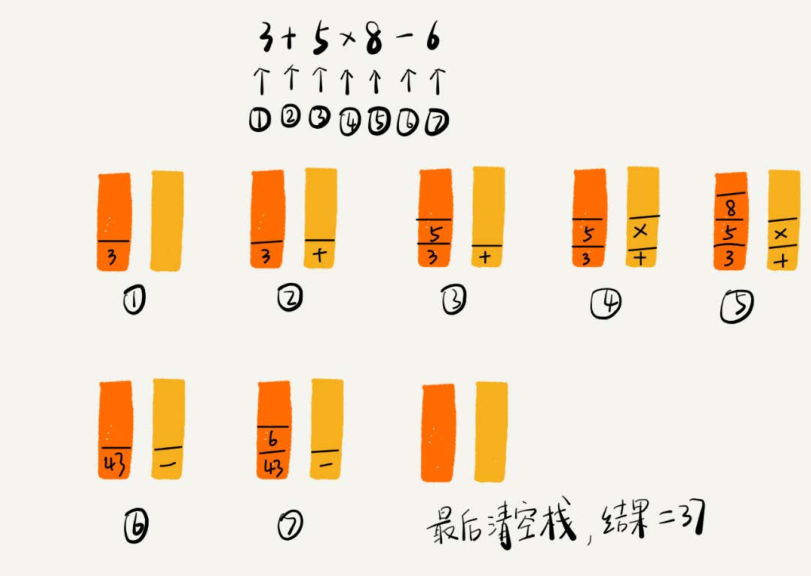
- 栈在表达式求值中的应用
- 如何实现浏览器的前进和后退功能?
- 队列
- 队列在线程池等有限资源池中的应用
- 第一种是非阻塞的处理方式,直接拒绝任务请求;
- 另一种是阻塞的处理方式,将请求排队,等到有空闲线程时,取出排队的请求继续处理。
- 理解:排队买票,先进先出
- 操作:只支持入队,出队

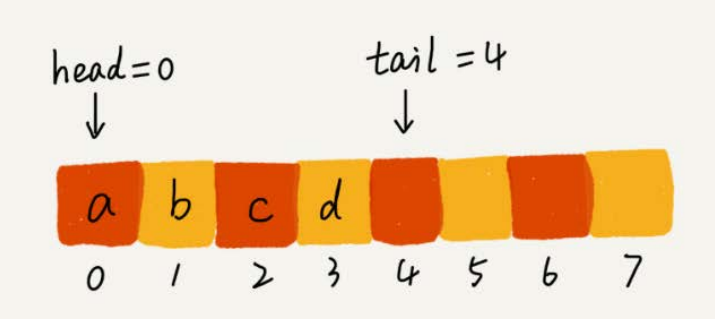
- 我们在出队时可以不用搬移数据。如果没有空闲空间了,我们只需要在入队时,再集中触发一次数据的搬移操作。
- 循环队列

- 循环队列会浪费一个数组的存储空间
- 阻塞队列
- 就是在队列为空的时候,从队头取数据会被阻塞。因为此时还没有数据可取,直到队列中有了数据才能返回;如果队列已经满了,那么插入数据的操作就会被阻塞,直到队列中有空闲位置后再插入数据,然后再返回。
- 并发队列
- 最简单直接的实现方式是直接在enqueue()、dequeue()方法上加锁,但是锁粒度大并发度会比较低,同一时刻仅允许一个存或者取操作
- 队列在线程池等有限资源池中的应用
- 递归
- 如何找到最终推荐人?
- 如何理解:
- .一个问题的解可以分解为几个子问题的解
- 这个问题与分解之后的子问题,除了数据规模不同,求解思路完全一样
- 存在递归终止条件
- 编写递归代码的关键是,只要遇到递归,我们就把它抽象成一个递推公式,不用想一层层的调用关系,不要试图用人脑去分解递归的每个步骤
- 递归代码限制最大深度,避免堆栈溢出
- 优点:写起来简洁
- 缺点:空间复杂度高,有堆栈溢出风险、存在重复计算、过多的函数调用会耗时较多等问题。
- 排序
- 为什么插入排序比冒泡排序更受欢迎?
- 基于比较的排序算法。
- 冒泡排序
- 操作相邻的两个数据
-
''' 冒泡排序:比较相邻元素,顺序错误就交换顺序 ''' def bubble_Sort(nums): for i in range(len(nums)-1): for j in range(len(nums)-1-i): if nums[j] > nums[j+1]: nums[j],nums[j+1] = nums[j+1],nums[j] return nums - 冒泡排序是原地排序算法吗?
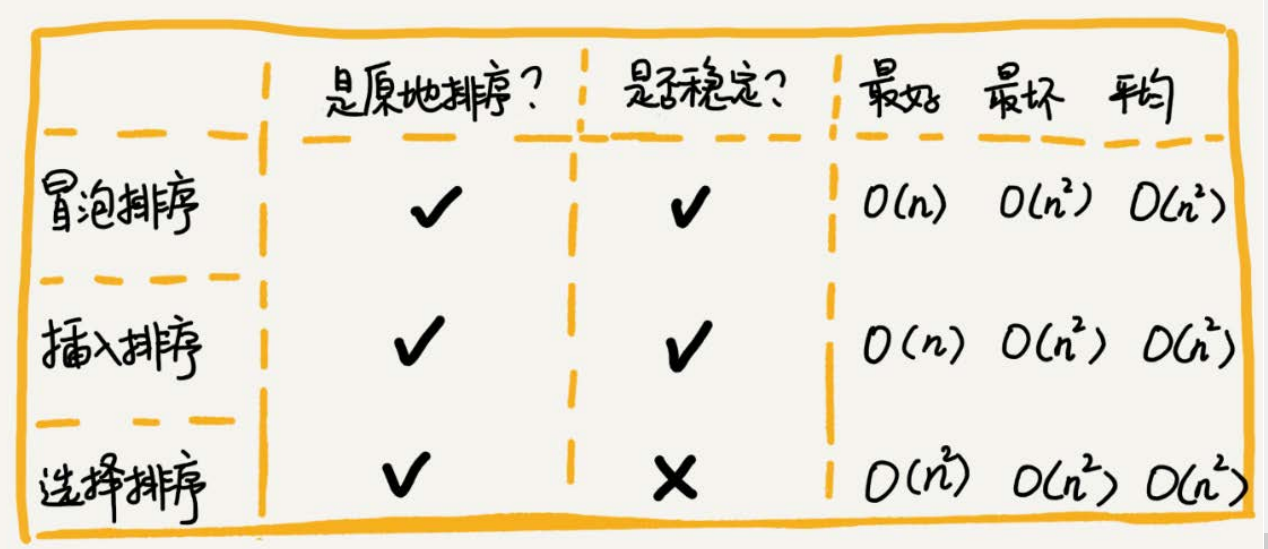
- 冒泡的过程只涉及相邻数据的交换操作,只需要常量级的临时空间,所以它的空间复杂度为 O(1) ,是一个原地排序算法
- 冒泡排序是稳定的排序算法吗?
-
在冒泡排序中,只有交换才可以改变两个元素的前后顺序。为了保证冒泡排序算法的稳定性,当有相邻的两个元素大小相等的时候,我们不做交换,相同大小的
数据在排序前后不会改变顺序,所以冒泡排序是稳定的排序算法。
-
-
冒泡排序的时间复杂度是多少?
-
最好情况下,要排序的数据已经是有序的了,我们只需要进行一次冒泡操作,就可以结束了,所以最好情况时间复杂度是 O(n) 。而最坏的情况是,要排序的数据
刚好是倒序排列的,我们需要进行n次冒泡操作,所以最坏情况时间复杂度为O(n 2 )。
-
-
插入排序---这个用的还是挺多的
-
''' 插入排序:假设元素左侧全部有序,找到自己的位置插入 ''' def insert_sort(nums): for i in range(1,len(nums)): for j in range(i,0,-1): if nums[j-1] <= nums[j]: break elif nums[j-1] > nums[j]: nums[j-1],nums[j] = nums[j],nums[j-1] return nums -
冒泡排序是原地排序算法吗?
-
从实现过程可以很明显地看出,插入排序算法的运行并不需要额外的存储空间,所以空间复杂度是 O(1) ,也就是说,这是一个原地排序算法。
-
-
插入排序的时间复杂度是多少?
-
如果要排序的数据已经是有序的,我们并不需要搬移任何数据。如果我们从尾到头在有序数据组里面查找插入位置,每次只需要比较一个数据就能确定插入的位
置。所以这种情况下,最好是时间复杂度为O(n)。注意,这里是从尾到头遍历已经有序的数据。
如果数组是倒序的,每次插入都相当于在数组的第一个位置插入新的数据,所以需要移动大量的数据,所以最坏情况时间复杂度为O(n 2 )。平均时间复杂度为O(n 2 )
-
-
-
选择排序
-
''' 选择排序:选择最小的,以此类推 ''' def select_Sort(nums): for i in range(len(nums)-1): for j in range(i+1,len(nums)): if nums[i] > nums[j]: nums[i],nums[j] = nums[j],nums[i] return nums -
排序是稳定的排序算法吗?
-
选择排序每次都要找剩余未排序元素中的最小值,并和前面的元素,交换位置,这样破坏了稳定性
-
-
- 快速排序
-
''' 快速排序:分而治之,一分为二进行排序 ''' def quick_sort(nums): if len(nums) <= 1: return nums s_nums = [] l_nums = [] #小于nums[0]放左边 for i in nums[1:]: if i < nums[0]: s_nums.append(i) else: # #大于nums[0]放右边 l_nums.append(i) #nums[0:1]是列表[],nums[0]是int数字 #连接左右列表加num[0:1] return quick_sort(s_nums)+nums[0:1]+quick_sort(l_nums) -
- 大部分情况下的时间复杂度都可以做到O(nlogn),只有在极端情况下,才会退化到O(n 2 )
- O(n)时间复杂度内求无序数组中的第K大元素?
- 冒泡排序
- 为什么插入排序比冒泡排序更受欢迎?
''' 快速排序:分而治之,一分为二进行排序'''import cProfileimport randomdef quick_sort(nums): if len(nums) <= 1: return nums s_nums = [] l_nums = [] #小于nums[0]放左边 for i in nums[1:]: if i < nums[0]: s_nums.append(i) else: # #大于nums[0]放右边 l_nums.append(i) #nums[0:1]是列表[],nums[0]是int数字 #连接左右列表加num[0:1] return quick_sort(s_nums)+nums[0:1]+quick_sort(l_nums)