NC13249-黑白树-(树上贪心)

链接：https://ac.nowcoder.com/acm/problem/13249
来源：牛客网

题目描述

一棵n个点的有根树，1号点为根，相邻的两个节点之间的距离为1。树上每个节点i对应一个值k[i]。每个点都有一个颜色，初始的时候所有点都是白色的。
你需要通过一系列操作使得最终每个点变成黑色。每次操作需要选择一个节点i，i必须是白色的，然后i到根的链上（包括节点i与根）所有与节点i距离小于k[i]的点都会变黑，已经是黑的点保持为黑。问最少使用几次操作能把整棵树变黑。

输入描述:

第一行一个整数n (1 ≤ n ≤ 10^5)
接下来n-1行，每行一个整数，依次为2号点到n号点父亲的编号。
最后一行n个整数为k[i] (1 ≤ k[i] ≤ 10^5)

样例解释:
对节点3操作，导致节点2与节点3变黑
对节点4操作，导致节点4变黑
对节点1操作，导致节点1变黑

输出描述:

一个数表示最少操作次数

示例1

输入

复制 

4
1
2
1
1 2 2 1

输出

复制 

3

---

总算遇到树上贪心的题了，虽然有点像dp

思路：看到树的题，第一想法往往就是先考虑dfs

往上涂色，叶子节点必须要涂，这一点无可非议。

父亲可能不用操作，儿子会帮忙涂好。

为了尽量选择少一些的点进行操作，应该从操作后往上涂色尽可能远的角度考虑，贪心思想。

如果操作儿子v比操作父亲u大得多，那就不要操作父亲，因为父亲能涂的，儿子都能包办，还要操作父亲干嘛？

如果儿子能往上涂的距离 小于 父亲，那也不一定要非要操作父亲，例如这种情况

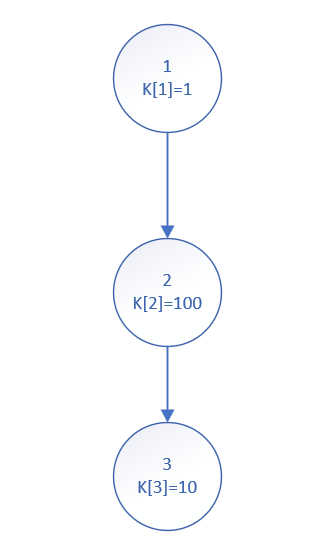
此时操作叶子节点3就行，不用再操作2。

但是选择往上涂色尽可能远这个贪心角度显然是对的。

通过dfs维护染色的最远距离，同时更新父亲涂色的最远距离。

当某一个点，开始涂色的儿子不能涂到这里，那就可能交给较近的儿子覆盖或者自己亲自涂，操作的节点数就要+1，这样可以避免贪心选择涂色距离远的而忽略了树的规模之类的问题。

#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<math.h>
#include<string>
#include<map>
#include<queue>
#include<stack>
#include<set>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;


vector<int>a[100086];
int f[100086];
int k[100086];
int cnt=0,n;


int dfs(int u)
{
    int now=0;
    for(int i=0;i<a[u].size();i++)
    {
        int v=a[u][i];
        now=max(now,dfs(v));
    }
    if(now<=0)
    {
        cnt++;///不管是谁往上涂的，反正不够了就要操作
        return k[u]-1;///返回的是当前涂色最远距离-1，返回往上继续涂的次数
    }
    k[ f[u] ] = max(k[ f[u] ],k[u]-1);///不论操作谁开始涂，维护父亲的最远距离

    return now-1;
}


int main()
{
    scanf("%d",&n);
    for(int i=2;i<=n;i++)
    {
        int x;
        scanf("%d",&x);
        a[x].push_back(i);///x的儿子是i
        f[i]=x;///i的父亲是x
    }
    for(int i=1;i<=n;i++)
        scanf("%d",&k[i]);
    dfs(1);
    printf("%d
",cnt);
    return 0;
}