python函数
一、递归(recursion)函数
在函数内部,可以调用其他函数。如果一个函数在内部调用自身本身,这个函数就是递归函数。
递归函数的特征:
- 必须有一个明确的结束条件
- 每次进入更深一层递归时,问题规模相比上次递归都应有所减少
- 相邻两次重复之间有紧密的联系,前一次要为后一次做准备(通常前一次的输出就作为后一次的输入)
一般来说,使用递归的都可以用循环来解决,比如:
# 求10!用循环
factorial = 1 for i in range(1, 11): factorial *= i print(factorial) # 3628800
#求10!用递归
def factorial(n):
if n == 1:
return 1
return n * factorial(n - 1)
print(factorial(10)) # 3628800
递归函数的优点是定义简单,逻辑清晰。
递归效率不高,递归层次过多会导致栈溢出(在计算机中,函数调用是通过栈(stack)这种数据结构实现的,每当进入一个函数调用,栈就会加一层栈帧,每当函数返回,栈就会减一层栈帧。由于栈的大小不是无限的,所以,递归调用的次数过多,会导致栈溢出)
print(factorial(1000)) #RecursionError: maximum recursion depth exceeded in comparison
解决栈溢出的方案设置栈的最大深度
import sys
sys.getrecursionlimit() # 显示栈的最大深度,默认是1000
sys.setrecursionlimit(10000) # 设置栈的最大深度
def factorial(n):
if n == 1:
return 1
return n * factorial(n - 1)
print(factorial(1000))
# 402387260077093773543702433923003985719374864210714632543799910429938512
# 398629020592044208486969404800479988610197196058631666872994808558901323
# 829669944590997424504087073759918823627727188732519779505950995276120874
# 9754624970436014182780946464962910563938874378864873371191810458257836478
# 4997701247663288983595573543251318532395846307555740911426241747434934755
# 3428646576611667797396668820291207379143853719588249808126867838374559731
# 7461360853795345242215865932019280908782973084313928444032812315586110369
# 76801357304216168747609675871348312025478589320767169132448426236131412508
# 78020800026168315102734182797770478463586817016436502415369139828126481021
# 30927612448963599287051149649754199093422215668325720808213331861168115536
# 15836546984046708975602900950537616475847728421889679646244945160765353408
# 19890138544248798495995331910172335555660213945039973628075013783761530712
# 77619268490343526252000158885351473316117021039681759215109077880193931781
# 14194545257223865541461062892187960223838971476088506276862967146674697562
# 91123408243920816015378088989396451826324367161676217916890977991190375403
# 127462228998800519544441428201218736174599264295658174662830295557029902432
# 415318161721046583203678690611726015878352075151628422554026517048330422614
# 397428693306169089796848259012545832716822645806652676995865268227280707578
# 139185817888965220816434834482599326604336766017699961283186078838615027946
# 595513115655203609398818061213855860030143569452722420634463179746059468257
# 3103790084024432438465657245014402821885252470935190620929023136493273497565
# 513958720559654228749774011413346962715422845862377387538230483865688976461927
# 3838149001407673104466402598994902222217659043399018860185665264850617997023
# 5619389701786004081188972991831102117122984590164192106888438712185564612496
# 079872290851929681937238864261483965738229112312502418664935314397013742853
# 1926649875337218940694281434118520158014123344828015051399694290153483077644
# 56909907315243327828826986460278986432113908350621709500259738986355427719674
# 28222487575867657523442202075736305694988250879689281627538488633969099598
# 26280956121450994871701244516461260379029309120889086942028510640182154399
# 4571568059418727489980942547421735824010636774045957417851608292301353580
# 81840096996372524230560855903700624271243416909004153690105933983835777939
# 4109700277534720000000000000000000000000000000000000000000000000000000000
# 0000000000000000000000000000000000000000000000000000000000000000000000000
# 00000000000000000000000000000000000000000000000000000000000000000000000000
# 00000000000000000000000000000000000000000000
优化递归,使用尾递归
尾递归是指,在函数返回的时候,调用自身本身,并且,return语句不能包含表达式。这样,编译器或者解释器就可以把尾递归做优化,使递归本身无论调用多少次,都只占用一个栈帧,不会出现栈溢出的情况。
def factorial(n, fact):
if n == 1:
return fact
return factorial(n - 1, n * fact)
print(factorial(20, 1))
# 2432902008176640000
递归运用 斐波那契数列
斐波那契数列,又称黄金分割数列,指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、……。
在数学上,费波那契数列是以递归的方法来定义:
F0 = 0 (n=0) F1 = 1 (n=1) Fn = F[n-1]+ F[n-2](n=>2)
斐波那契数列可以使用循环或递归来实现
1、循环
def fibonacci(n):
a = 1
b = 1
for i in range(n - 1):
a, b = b, a + b
return a
print(fibonacci(10))
2、递归
def fibonacci(n):
if n==1 or n==2:
return 1
return fibonacci(n-1)+fibonacci(n-2)
print(fibonacci(10))
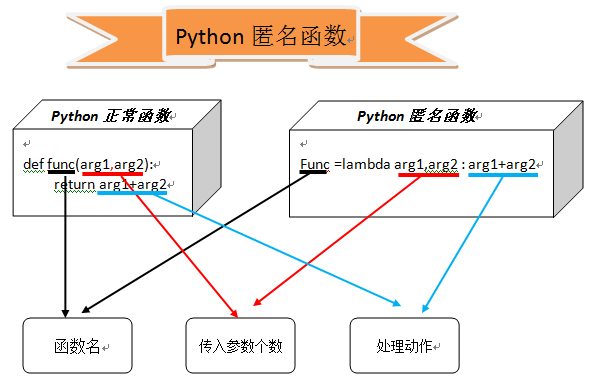
二、匿名函数
1、匿名函数介绍
在Python中,不通过def来声明函数名字,而是通过lambda关键字来定义的函数称为匿名函数。
lambda函数能接收任何数量(可以是0个)的参数,但只能返回一个表达式的值,lambda函数是一个函数对象,直接赋值给一个变量,这个变量就成了一个函数对象。
2、语法
lambda 参数:表达式
先写lambda关键字,然后依次写匿名函数的参数,多个参数中间用逗号连接,然后是一个冒号,冒号后面写返回的表达式。
sum=lambda x,y:x+y sum(2,3)
使用lambda函数可以省去函数的定义,不需要声明一个函数然后使用,而可以在写函数的同时直接使用函数。
3、匿名函数使用场景
a、需要将一个函数对象作为参数来传递时,可以直接定义一个lambda函数(作为函数的参数或返回值)
b、要处理的业务符合lambda函数的情况(任意多个参数和一个返回值),并且只有一个地方会使用这个函数,不会在其他地方重用,可以使用lambda函数
c、与一些Python的内置函数配合使用,提高代码的可读性
4、匿名函数的使用
a、sort排序:(字典value排序)
students=[
{'name':'zhangsan','age':18},
{'name':'lisi','age':20},
{'name':'wangwu','age':19},
{'name':'zhaoliu','age':17},
]
students.sort(key=lambda ele:ele['age'])
print(students)
b、filter(函数,Iterable)
ages=[12,37,27,43,32] x=list(filter(lambda ele:ele>30,ages)) print(x) #[37,43,32]
c、map(函数,Iterable)
li = [1,2,3,4,5] print(list(map(lambda x:x*x,li))) #[1,4,9,16,25]
d、reduce(函数,Iterable)
reduce()把一个函数作用在一个序列[x1, x2, x3, ...]上,这个函数必须接收两个参数,reduce把结果继续和序列的下一个元素做运算,其效果就是:
reduce(func([1,2,3])) 等同于 func(func(1,2),3)
from functools import reduce li = [1,2,3,4,5,6,7,8,9] print(reduce(lambda x,y:x * y,li)) # 结果=1*2*3*4*5*6*7*8*9 = 362880
students=[
{'name':'zhangsan','age':18},
{'name':'lisi','age':20},
{'name':'wangwu','age':19},
{'name':'zhaoliu','age':17},
]
reduce(lambda x,y:x+y['age'],students,0) #求age累加和