Divisions
David is a young boy and he loves numbers. Recently he learned how to divide two numbers.David divides the whole day. He is happy if the result of the division is an integer, but he is not very amused if this is not the case. After quite a while he decided to use only a single dividend each day.
The parents of David are very careful and they would like to ensure that David experiences enough happiness. Therefore they decide which number David will use as the dividend for this day.
There is still a problem: The parents are not very good at math and don’t know how to calculatethe number of positive integral divisors for a given dividend N , which lead to an integral result.Now it’s up to you to help David’s parents.
Input
The single input line contains the single integer N , where N is chosen as a dividend (1≤N≤1018)
Output
Print the number of positive integral divisors of N that lead to an integral result of the division.
sample input 1
12
sample output 1
6
sample input 2
999999999999999989
sample output 2
2
sample input 3
100000007700000049
sample output 3
4
大数素因子分解
#include <iostream> #include <algorithm> #include <cstring> #include <cstdio> #include <vector> #include <queue> #include <stack> #include <cstdlib> #include <iomanip> #include <cmath> #include <cassert> #include <ctime> #include <map> #include <set> using namespace std; #pragma comment(linker, "/stck:1024000000,1024000000") #define lowbit(x) (x&(-x)) #define max(x,y) (x>=y?x:y) #define min(x,y) (x<=y?x:y) #define MAX 100000000000000000 #define MOD 1000000007 #define pi acos(-1.0) #define ei exp(1) #define PI 3.1415926535897932384626433832 #define ios() ios::sync_with_stdio(true) #define INF 0x3f3f3f3f #define mem(a) (memset(a,0,sizeof(a))) typedef long long ll; const int s=8; char ch[26]; ll mult_mod(ll a,ll b,ll c) { a%=c; b%=c; ll ret=0; ll tmp=a; while(b) { if(b&1){ ret+=tmp; if(ret>c) ret-=c; } tmp<<=1; if(tmp>c) tmp-=c; b>>=1; } return ret; } ll pow_mod(ll a,ll n,ll mod) { ll ans=1; ll tmp=a%mod; while(n) { if(n&1) ans=mult_mod(ans,tmp,mod); tmp=mult_mod(tmp,tmp,mod); n>>=1; } return ans; } bool check(ll a,ll n,ll x,ll t) { ll ret=pow_mod(a,x,n); ll last=ret; for(int i=1;i<=t;i++) { ret=mult_mod(ret,ret,n); if(ret==1 && last!=1 && last!=n-1) return true; last=ret; } if(ret!=1) return true; else return false; } bool miller_pabin(ll n) { if(n<2) return false; if(n==2) return true; if((n&1)==0) return false; ll x=n-1; ll t=0; while((x&1)==0) {x>>=1;t++;} srand(time(NULL)); for(int i=0;i<s;i++){ ll a=rand()%(n-1)+1; if(check(a,n,x,t)) return false; } return true; } ll factor[110]; int tol=0; ll gcd(ll a,ll b) { ll t; while(b) { t=a; a=b; b=t%b; } if(a>=0) return a; else return -a; } ll pollard_rho(ll x,ll c) { ll i=1,k=2; srand(time(NULL)); ll x0=rand()%(x-1)+1; ll y=x0; while(1) { i++; x0=(mult_mod(x0,x0,x)+c)%x; ll d=gcd(y-x0,x); if(d!=1 && d!=x) return d; if(y==x0) return x; if(i==k){y=x0;k+=k;} } } void findfac(ll n,ll k) { if(n==1) return ; if(miller_pabin(n)) { factor[tol++]=n; return ; } ll p=n; ll c=k; while(p>=n) p=pollard_rho(p,c--); findfac(p,k); findfac(n/p,k); } int main() { ll n; scanf("%lld",&n); if(miller_pabin(n)) printf("2 "); else { findfac(n,107); ll ans=1; for(int i=0;i<tol;i++) { //printf("%lld ",factor[i]); ll pos=0; while(n>0 && (n%factor[i]==0)) { pos++; n/=factor[i]; } printf("%lld %lld ",factor[i],pos); if(pos) ans*=(pos+1); } printf("%lld ",ans); } return 0; }
Extreme Sort
John likes sorting algorithms very much. He has studied quick sort, merge sort, radix sort, and many more.
A
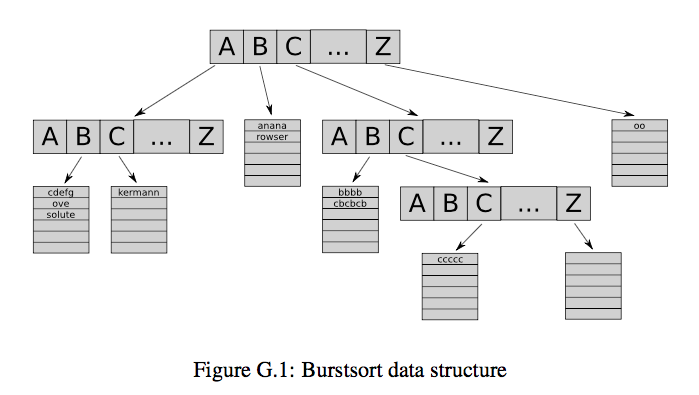
long time ago he has written a lock-free parallel string sorting
program. It was a combination of burst sort and multi-key quick sort. To
implement burst sort you need to build a tree of buckets.For each input
string you walk through the tree and insert part of the string into the
right bucket.When a bucket fills up, it "bursts" and becomes a new
subtree (with new buckets).
Well, enough about the past. Today John is playing with sorting algorithms again. This time it’s numbers. He has an idea for a new algorithm, “extreme sort”. It’s extremely fast, performance levels are OVER NINETHOUSAND. Before he tells anyone any details, he wants to make sure that it works correctly.
Your task is to help him and verify that the so-called extreme property holds after the first phase of the algorithm. The extreme property is defined as min (xi,j ) ≥ 0, where
Input
The first line contains a single integer N (1 ≤ N ≤ 1024). The second line contains N integers a1 a2 ... aN (1≤ai ≤1024).
Output
Print one line of output containing “yes” if the extreme property holds for the given input, “no”otherwise.
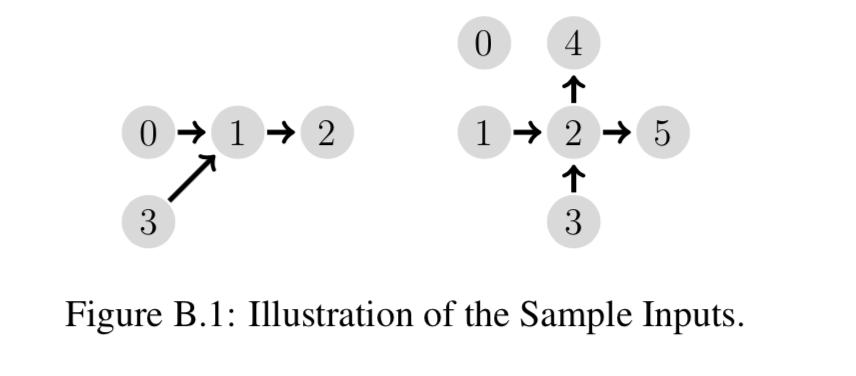
样例输入1
2 1 2
样例输出1
yes
样例输入2
4 2 1 3 4
样例输出2
no
只要判断是否严格递增就可以了
#include <iostream> using namespace std; #include <cstdio> typedef unsigned long long ull; typedef long long ll; int main() { int front=0,last,ok=0,n; scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&last); if(last<front) ok=1; front=last; } puts(ok?"no":"yes"); return 0; }
Legacy Code
Once again you lost days refactoring code, which never runs in the first place. Enough is enough– your time is better spent writing a tool that finds unused code!
Your software is divided into packages and executables. A package is a collection of methods. Executables are packages defining among other methods exactly one method with namePROGRAM. This method is executed on the start of the corresponding executable. Ordinary packages have no method named PROGRAM.
Each method is uniquely identified by the combination of package and method names. E.g.the method with the identifier SuperGame::PROGRAM would be the main method of the executable SuperGame.
For
every method in your software you are given a list of methods directly
invoking it. Thus you can easily identify methods, that are never called
from any method. However, your task is more challenging: you have to
find unused methods. These are methods that are never reached by the
control flow of any executable in your software.
Input
The first line of the input contains an integer N, the number of methods in your software(1≤N ≤400).
Each method is described by two lines, totaling in 2 · N lines. The first line consists of the unique identifier of the method and ki, the number of methods directly invoking this one (0 ≤ ki ≤ N).The second line consists of a set of ki identifiers of these calling methods or is empty if there are no such methods, i.e. ki = 0.
Method identifiers consist of a package name followed by two colons and a method name like Packagename::Methodname. Both strings, the package and the method name, each consist of up to 20 lowercase, uppercase characters or digits (a-z, A-Z, 0-9).
There will be exactly N different method identifiers mentioned in the input.
Output
A line containing the number of unused methods in your software.
样例输入1
2 SuperGame::PROGRAM 0 HelpPackage::HelpFunction 2 HelpPackage::HelpFunction SuperGame::PROGRAM
样例输出1
0
样例输入2
2 Loop::CallA 1 Loop::CallB Loop::CallB 1 Loop::CallA
样例输出2
2
看懂英文就可以过,可以本身救赎尚可执行文件或者间接可执行
#include <iostream> #include <algorithm> #include <cstring> #include <cstdio> #include <vector> #include <queue> #include <stack> #include <cstdlib> #include <iomanip> #include <cmath> #include <cassert> #include <ctime> #include <map> #include <set> using namespace std; #pragma comment(linker, "/stck:1024000000,1024000000") #pragma GCC diagnostic error "-std=c++11" #define lowbit(x) (x&(-x)) #define max(x,y) (x>=y?x:y) #define min(x,y) (x<=y?x:y) #define MAX 100000000000000000 #define MOD 1000 #define pi acos(-1.0) #define ei exp(1) #define PI 3.1415926535897932384626433832 #define ios() ios::sync_with_stdio(true) #define INF 0x3f3f3f3f #define mem(a) (memset(a,0,sizeof(a))) typedef unsigned long long ull; string s,ss[406]; vector<int>v[1006]; map<string,int>m; int n,k,pos=0,vis[1006]; int getname(string s) { if(!m[s]) { ++pos; m[s]=pos; if(s.find("::PROGRAM")==s.size()-9 && s.size()>=10) vis[pos]=1; } return m[s]; } void dfs(int now) { vis[now]=1; for(auto t:v[now]) if(!vis[t]) dfs(t); } int main() { scanf("%d",&n); for(int i=0;i<n;i++) { cin>>ss[i]>>k; int f=getname(ss[i]); for(int j=0;j<k;j++) { cin>>s; int l=getname(s); v[l].push_back(f); } } for(int i=1;i<=pos;i++) if(vis[i]) dfs(i); int ans=0; for(int i=0;i<n;i++) if(vis[getname(ss[i])]) ans++; printf("%d ",n-ans); return 0; } /* 5 loop::PROGRAM 3 loop::xy loop::zy loop::wz loop::xy 2 loop::zy loop::wz loop::zy 1 loop::yz loop::www 1 loop::wz loop::wz 0 4 */
Last night, I must have dropped my alarm clock. When the alarm went off in the morning, it showed 51:80 instead of 08:15. This made me realize that if you rotate a seven segment display like it is used in digital clocks by 180 degrees, some numbers still are numbers after turning them upside down.
As you can see,
My favourite numbers are primes, of course. Your job is to check whether a number is a prime and still a prime when turned upside down.
Input
One line with the integer N in question (1 ≤ N ≤ 1016). N will not have leading zeros.
Output
Print one line of output containing “yes” if the number is a prime and still a prime if turned upside down, “no” otherwise.
样例输入1
151
样例输出1
yes
样例输入2
23
样例输出2
no
样例输入3
18115211
样例输出3
no
正反都是素数,要是包含3,4,7一定不是
#include <iostream> #include <algorithm> #include <cstring> #include <cstdio> #include <vector> #include <queue> #include <stack> #include <cstdlib> #include <iomanip> #include <cmath> #include <cassert> #include <ctime> #include <map> #include <set> using namespace std; #pragma comment(linker, "/stck:1024000000,1024000000") #define lowbit(x) (x&(-x)) #define max(x,y) (x>=y?x:y) #define min(x,y) (x<=y?x:y) #define MAX 100000000000000000 #define MOD 1000000007 #define pi acos(-1.0) #define ei exp(1) #define PI 3.1415926535897932384626433832 #define ios() ios::sync_with_stdio(true) #define INF 0x3f3f3f3f #define mem(a) (memset(a,0,sizeof(a))) typedef long long ll; const int s=8; char ch[26]; ll mult_mod(ll a,ll b,ll c) { a%=c; b%=c; ll ret=0; ll tmp=a; while(b) { if(b&1){ ret+=tmp; if(ret>c) ret-=c; } tmp<<=1; if(tmp>c) tmp-=c; b>>=1; } return ret; } ll pow_mod(ll a,ll n,ll mod) { ll ans=1; ll tmp=a%mod; while(n) { if(n&1) ans=mult_mod(ans,tmp,mod); tmp=mult_mod(tmp,tmp,mod); n>>=1; } return ans; } bool check(ll a,ll n,ll x,ll t) { ll ret=pow_mod(a,x,n); ll last=ret; for(int i=1;i<=t;i++) { ret=mult_mod(ret,ret,n); if(ret==1 && last!=1 && last!=n-1) return true; last=ret; } if(ret!=1) return true; else return false; } bool miller_pabin(ll n) { if(n<2) return false; if(n==2) return true; if((n&1)==0) return false; ll x=n-1; ll t=0; while((x&1)==0) {x>>=1;t++;} srand(time(NULL)); for(int i=0;i<s;i++){ ll a=rand()%(n-1)+1; if(check(a,n,x,t)) return false; } return true; } int main() { ll x=0,y=0; scanf("%s",&ch); int k=strlen(ch); for(int i=0;i<k;i++) { if(ch[i]=='3' || ch[i]=='4' || ch[i]=='7') { printf("no "); return 0; } x=x*10+(ch[i]-'0'); } for(int i=k-1;i>=0;i--) { if(ch[i]=='0' || ch[i]=='1' || ch[i]=='2' || ch[i]=='5' || ch[i]=='8') y=y*10+(ch[i]-'0'); else if(ch[i]=='6') y=y*10+9; else if(ch[i]=='9') y=y*10+6; } bool okx=miller_pabin(x); bool oky=miller_pabin(y); if(okx && oky) printf("yes "); else printf("no "); return 0; }
Milling machines
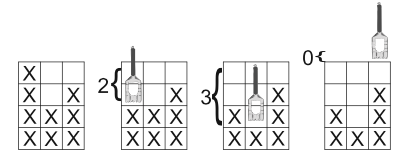
A fab lab is an open, small-scale workshop where you can create or fabricate almost anything you want mostly by using computer controlled tools like a laser cutter or a 3D printer. The FAU fab lab recently got a CNC milling machine. Using the milling machine you can cut or remove material with different tools from the surface of a workpiece. It is controlled via a computer program.
I sometimes wondered what happens if multiple different shaped workpieces are sent through the same milling program. For simplification assume that we have only two dimensional workpieces without holes. A milling program consists of multiple steps; each step describes where the milling machine has to remove material (using different tools) from the top of the surface.
Input
The first line consists of two integers W and S, where W gives the number of workpieces andS the number of steps in the milling program (1 ≤ W, S ≤ 10410^4104). The next line consists of two integers X and Y , where X gives the width and Y gives the maximal possible height of workpieces (1 ≤ X, Y ≤ 100).
Then follow W lines, each describing one workpiece. Each workpiece description consists of X non-negative integers specifying the surface height in that column.
Then follow S lines, each describing one milling step of the milling program. Each milling step description consists of X non-negative integers si (0 ≤ si ≤ Y ) specifying the amount of surface to cut off in each column (relative to the height of the milling area, i.e. Y , not relative to the top of the workpiece). See Fig. I.1 for details.
Output
For each workpiece, output one line containing X integers specifying the remaining surface heights (in the same order as in the input).
Figure I.1: Second workpiece in first sample: initial workpiece followed by milling in each column – the value in the milling program determines the vertical position of the cutter head.
样例输入1
2 1 3 4 4 4 4 4 2 3 2 3 0
样例输出1
2 1 4 2 1 3
样例输入2
1 3 10 100 11 22 33 44 55 66 77 88 99 100 1 100 1 100 1 100 1 100 1 100 58 58 58 58 58 58 58 58 58 58 42 42 42 42 42 42 42 42 66 42
样例输出2
11 0 33 0 42 0 42 0 34 0
也是比较水的一道题
#include <iostream> #include <cstdio> using namespace std; int a[15000][105]; int b[15000],w,s,x,y; typedef long long ll; int main() { scanf("%d%d%d%d",&w,&s,&x,&y); for(int i=0;i<w;i++) for(int j=0;j<x;j++) scanf("%d",&a[i][j]); int ans; for(int i=0;i<s;i++) for(int j=0;j<x;j++) { scanf("%d",&ans); b[j]=max(b[j],ans); } for(int i=0;i<w;i++) { for(int j=0;j<x;j++) { printf("%d", a[i][j]>y-b[j]?y-b[j]:a[i][j]); if(j!=x-1) printf(" "); } if(i!=w-1) printf(" "); } return 0; }
Bounty Hunter II
Spike the bounty hunter is tracking another criminal through space. Luckily for him hyperspace travel has made the task of visiting several planets a lot easier. Each planet has a number of Astral Gates; each gate connects with a gate on another planet. These hyperspace connections are, for obvious safety reasons, one-way only with one gate being the entry point and the other gate being the exit point from hyperspace. Furthermore, the network of hyperspace connections must be loop-free to prevent the Astral Gates from exploding, a tragic lesson learned in the gate accident of 2022 that destroyed most of the moon.
While looking at his star map Spike wonders how many friends he needs to conduct a search on every planet. Each planet should not be visited by more than one friend otherwise the criminal might get suspicious and flee before he can be captured. While each person can start at a planet of their choosing and travel along the hyperspace connections from planet to planet they are still bound by the limitations of hyperspace travel.
Input Format
The input begins with an integer NNN specifying the number of planets (0<N≤1000). The planets are numbered from 0 to N−1. The following N lines specify the hyperspace connections.
The i-th of those lines first contains the count of connections K (0≤K≤N−1) from planet iii followed by K integers specifying the destination planets.
Output Format
Output the minimum number of persons needed to visit every planet.
样例输入1
4 1 1 1 2 0 1 1
样例输出1
2
样例输入2
6 0 1 2 2 4 5 1 2 0 0
样例输出2
4
匈牙利匹配
#include <iostream> #include <algorithm> #include <cstring> #include <cstdio> #include <vector> #include <queue> #include <stack> #include <cstdlib> #include <iomanip> #include <cmath> #include <cassert> #include <ctime> #include <map> #include <set> using namespace std; #pragma comment(linker, "/stck:1024000000,1024000000") #pragma GCC diagnostic error "-std=c++11" #define lowbit(x) (x&(-x)) #define max(x,y) (x>=y?x:y) #define min(x,y) (x<=y?x:y) #define MAX 100000000000000000 #define MOD 1000 #define pi acos(-1.0) #define ei exp(1) #define PI 3.1415926535897932384626433832 #define ios() ios::sync_with_stdio(true) #define INF 0x3f3f3f3f #define mem(a) (memset(a,0,sizeof(a))) typedef unsigned long long ull; typedef long long ll; int n,k,x; int vis[2005],pos[2005]; vector<int>v[2005]; int dfs(int now) { if(vis[now]) return 0; vis[now]=1; for(auto &t:v[now]) { if(pos[t]==-1 || dfs(pos[t])) { pos[t]=now; return 1; } } return 0; } int solve() { int ans=0; memset(pos,-1,sizeof(pos)); for(int i=0;i<n;i++) { memset(vis,0,sizeof(vis)); ans+=dfs(i); } return ans; } int main() { scanf("%d",&n); for(int i=0;i<n;i++) { scanf("%d",&k); for(int j=0;j<k;j++) { scanf("%d",&x); v[i].push_back(x+n); } } printf("%d ",n-solve()); return 0; } /* 5 3 2 3 4 1 2 0 0 0 */