算法19可见的山峰对数量(单调栈)

描述

一个不含有负数的数组可以代表一圈环形山，每个位置的值代表山的高度。比如，{3,1,2,4,5}，{4,5,3,1,2}或{1,2,4,5,3}都代表同样结构的环形山。3->1->2->4->5->3 方向叫作 next 方向(逆时针)，3->5->4->2->1->3 方向叫作 last 方向(顺时针)。

山峰 A 和 山峰 B 能够相互看见的条件为:

1. 如果 A 和 B 是同一座山，认为不能相互看见。

2. 如果 A 和 B 是不同的山，并且在环中相邻，认为可以相互看见。

3. 如果 A 和 B 是不同的山，并且在环中不相邻，假设两座山高度的最小值为 min。如果 A 通过 next 方向到 B 的途中没有高度比 min 大的山峰，或者 A 通过 last 方向到 B 的途中没有高度比 min 大的山峰，认为 A 和 B 可以相互看见。

问题如下：

给定一个含有负数可能有重复值的数组 arr，请问有多少对山峰能够相互看见？ 

输入描述：

第一行给出一个整数 n，表示山峰的数量。
以下一行 n 个整数表示各个山峰的高度。

输出描述：

输出一行表示答案。

示例1

输入：
5
3 1 2 4 5

输出：
7

思路

两个阶段：

1. 遍历阶段：

首先找到一个最大值进行存储，然后按照next方向遍历，不断压栈，如果某个记录(X,K)从栈中弹出了，产生可见山峰对的数量为：

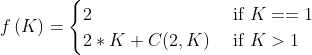
2. 清算阶段:

单独清算栈中记录的阶段，分为三个小阶段

第1个小阶段：弹出的记录不是栈中最后一个记录，也不是倒数第二个记录，此时产生山峰对为：

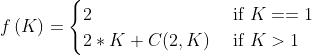
第2个小阶段：弹出的记录是栈中倒数第二个记录（X,K），需要查看栈中最后一条记录（Y,M),此时产生山峰对为：

第3个小阶段：弹出的记录是栈中倒数第一个记录(X,K),此时产生的山峰对为：

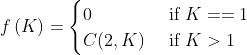
解释：2*K(每个节点会有两个山峰对)和1*K(当位于清算阶段的第2个小阶段时，对外能看见的山峰只有最大山峰，并且只有一个，因此每个节点只有一个山峰对)表示，当前节点对外产生的山峰对; C(2,K)表示当前节点内部产生的山峰对。

代码如下：

import java.util.Scanner;
import java.util.Stack;

public class Main{
    
//新建类去承载需要的没做山的高度以及次数
public static class Record {
    public int value;
    public int times;
    public Record (int value){
        this.value = value;
        this.times = 1;
    }
}

    //如果k==1，返回0；如果k>1，返回C(2,k)
    public static int getInternalSum(int k){
        return k==1?0:(k*(k-1)/2);
    }
    
    //环形数组中当前位置为i，数组长度为size，返回i的下一个位置
    public static int nextIndex(int i, int size){
        return i<(size-1)?(i+1):0;
    }
    
    public static int getVisibleNum(int[] arr){
        if(arr==null||arr.length<2){
            return 0;
        }
        int size=arr.length;
        int maxIndex=0;
        //先在换种找到一个最大值的位置，哪一个都可以
        for(int i=0;i<size;i++){
            maxIndex=arr[maxIndex]<arr[i]?i:maxIndex;
        }
        Stack<Record> stack=new Stack<Record>();
        //先把(最大值,1)这个记录放入stack中
        stack.push(new Record(arr[maxIndex]));
        //从最大值位置的下一个位置开始沿next方向遍历
        int index=nextIndex(maxIndex,size);
        //用“小找大”的方式统计所有可见山峰对
        int res=0;
        //遍历阶段开始，当index再次回到maxIndex的时候，说明转了一圈，遍历阶段就结束
        while(index != maxIndex){
            //当前数字arr[index]要进栈，判断会不会破坏第一维度的数字从顶到底依次变大
            //如果破坏了，就依次弹出栈顶记录，并计算山峰对数量
            while(stack.peek().value < arr[index]){
                int k = stack.pop().times;
                //弹出记录为(X,K),如果K==1,产生2对
                //如果K>1,产生2*K+C(2,K)对
                res+=getInternalSum(k)+2*k;
            }
            //当前数字arr[index]要进入栈了，如果和当前栈顶数字一样就合并
            //不一样就把记录(arr[index],1)放入栈中
            if(stack.peek().value==arr[index]){
                stack.peek().times++;
            }else{
                stack.push(new Record(arr[index]));
            }
            index=nextIndex(index,size);
        }
        //清算阶段
        //清算阶段第1小阶段
        while(stack.size()>2){
            int times=stack.pop().times;
            res+=getInternalSum(times)+2*times;
        }
        //清算阶段第2小阶段
        if(stack.size()==2){
            int times=stack.pop().times;
            res+=getInternalSum(times)+(stack.peek().times==1?times:2*times);
        }
        //清算阶段第3小阶段
        res+=getInternalSum(stack.pop().times);
        return res;
    }
    
    public static void main (String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int[] arr = new int[n];
        for (int i = 0; i < n; i++) {
            arr[i] = sc.nextInt();
        }
        int result = getVisibleNum(arr);
        System.out.println(result);
    }
}