题目如下:

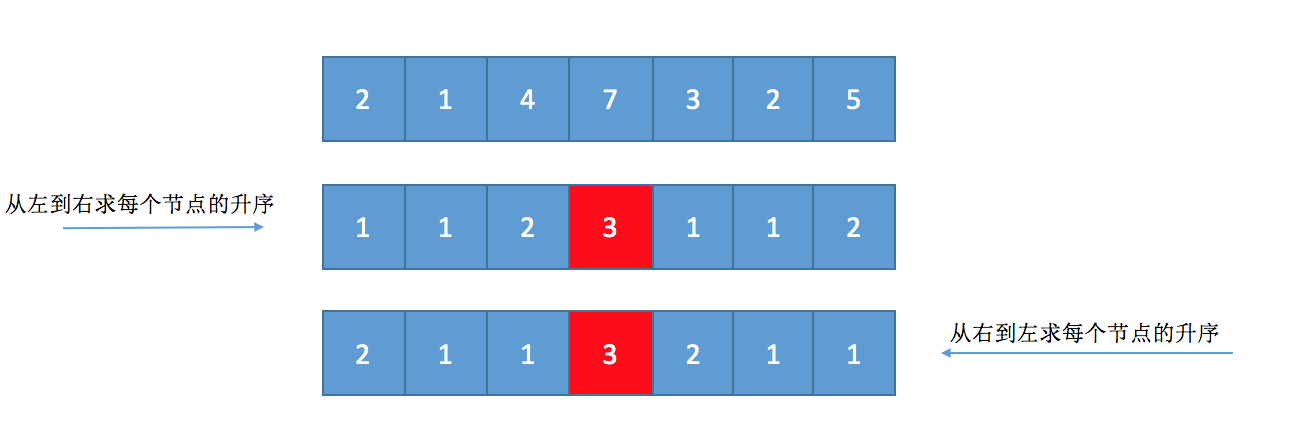
解题思路:本题的关键是找出从升序到降序的转折点。开到升序和降序,有没有联想的常见的一个动态规划的经典案例--求最长递增子序列。对于数组中每一个元素的mountain length就是左边升序的子序列长度加上右边降序的左序列长度。对于右边降序,如果我们遍历数组,那么降序就是升序。那么我们要做的就是,分别正序和倒序遍历数组,求出每个元素的左边和右边升序的子序列长度,那么这个长度的和就是答案。如下图,我们分别用两个数组保持正序和逆序遍历时候,每个元素在当前所属的递增子序列中的长度位置,如果非递增则记为1。求出所有元素的长度位置后,对于任意一个元素,其mountain length = dp[正序] + dp[倒序] - 1 (dp[正序] != 1 && dp[倒序] != 1)。
代码如下:
class Solution(object): def longestMountain(self, A): """ :type A: List[int] :rtype: int """ dp_order = [1 for x in xrange(len(A))] dp_reverse = [1 for x in xrange(len(A))] for i in xrange(1,len(A)): if A[i] > A[i-1] : dp_order[i] = dp_order[i-1] + 1 for i in xrange(-1,-len(A),-1): if A[i] < A[i-1] : dp_reverse[i-1] = dp_reverse[i] + 1 res = 0 for v1,v2 in zip(dp_order,dp_reverse): if v1 != 1 and v2 != 1: res = max(res,v1+v2-1) #print dp_order #print dp_reverse return res