1 #include <stdio.h> 2 #include <stdlib.h> 3 4 #define OK 1 5 #define ERR 2 6 #define TRUE 1 7 #define FALSE 0 8 #define MAXSIZE 4 //定义队列的最大长度 9 10 typedef int status; //定义函数返回的状态,OK & ERR 11 typedef char datatype; //定义队列中每个元素的数据类型,这里暂定为字符型 12 13 typedef struct { 14 datatype data[MAXSIZE]; //存储着队列中的每个元素 15 int front, rear; //头指针和尾指针 16 /* 17 假设用于模拟队列的数组长度为8,规定入队和出队方向都向左(即下标0的元素始终用于出队),有一个指针end永远标识队尾元素的下标,当end=0时表示队列只有一个元素,当end=-1时标识队列为空,类似于栈的top指针, 18 现在入队3个元素,数组如下, 19 A B C _ _ _ _ _ 指针end=2 20 出队1个元素,即下标是0的元素出队,也就是A, 21 _ B C _ _ _ _ _ 指针end=2 22 这时下标0的元素为空,需要将后面的元素都前移,然后将指针end-1,如果队列很长,这个操作会带来很大开销,所以我们不应该用栈的固定思维去思考队列,也就是说队头不一定要在下标为0的位置, 23 这样一来我们定义一个指针front用来表示队头所在元素的下标,再定义一个指针rear用来表示队尾所在元素的下一个元素的下标,当front=rear时表示队列为空,这就是队列的初始状态, 24 现在我们用上述队列的存储结构来创建一个新队列, 25 _ _ _ _ _ _ _ _ 指针front=0 指针rear=0 26 入队3个元素, 27 A B C _ _ _ _ _ 指针front=0 指针rear=3 28 出队1个元素, 29 _ B C _ _ _ _ _ 指针front=1 指针rear=3 30 再入队3个元素, 31 _ B C D E F _ _ 指针front=1 指针rear=6 32 再出队3个元素, 33 _ _ _ _ E F _ _ 指针front=4 指针rear=6 34 可见新定义的队列的存储结构不需要大量前移元素了(因为队头元素由指针front唯一确定),这样,入队只需要rear+1,出队只需要front+1, 35 但是又出现了个很严重的问题:当继续入队2个(G和H)元素,H元素便成为数组的最后一个元素,此时rear=8,而下标为8的位置是越界的,而数组最前面的下标(0~3,共4个)却空着,就造成了浪费,这种现象叫做假溢出, 36 要解决上述问题,可将队列的头和尾相连,使之成为循环队列, 37 当数组的最后一个元素也被使用了,此时可将rear等于0而不是8, 38 _ _ _ _ E F G H 指针front=4 指针rear=0 39 这时,再入队3个元素,数组如下, 40 I J K _ E F G H 指针front=4 指针rear=3 41 我们将循环队列的这种情况称为队列已满(rear和front之间空一个元素),不然再入队一个元素(L),那么rear=4,和front相等了,这时是空队列呢还是满队列呢? 42 循环队列已满的条件:(rear+1)%QueueSize == front 43 循环队列长度公式:(rear-front+QueueSize)%QueueSize 44 入队(rear后移一位):rear=(rear+1)%QueueSize 45 出队(front后移一位):front=(front+1)%QueueSize 46 其中QueueSize是队列的最大长度(数组的长度),比如上面演示的队列的QueueSize就是8 47 循环队列长度公式的由来,(以下讨论的数都是整数) 48 当rear>front时,队列的长度:rear-front,其中rear-front必然是正数 49 当rear<front时,队列的长度由两部分组成, 50 第一部分是(空元素的后面):QueueSize-front 51 第二部分是(空元素的前面):0+rear 52 综上,队列的长度:rear-front+QueueSize,其中rear-front必然是负数 53 如果rear-front+QueueSize这个公式用于rear>front的队列,那么得到的队列长度就大于数组的最大长度(QueueSize), 54 那到底大了多少呢,其实就是大了QueueSize,但我们又不能减去QueueSize,这样就不能计算rear<front的队列长度, 55 正确解决方法是对rear-front+QueueSize取余,模数是QueueSize,即(rear-front+QueueSize)%QueueSize, 56 这样, 57 对于rear>front,虽然先加上了QueueSize,但最后的结果模上了QueueSize,相当于抵消了之前加的QueueSize 58 对于rear<front,由于rear-front必然是负数,但这个负数是大于-QueueSize的(这个负数的最小值是-QueueSize+1),所以rear-front+QueueSize的范围是[1,QueueSize-1],对这个区间里的任何一个数模上QueueSize还是这个数本身 59 其实对rear-front+QueueSize模上QueueSize是为了兼容rear>front的队列 60 61 */ 62 } SequenceQueue; 63 64 /* 函数原型,队列的基本操作,与栈相同 */ 65 SequenceQueue *createSequenceQueue(void); 66 status isEmpty(SequenceQueue *L); 67 void clear(SequenceQueue *L); 68 datatype getTop(SequenceQueue *L); 69 int getLength(SequenceQueue *L); 70 status push(SequenceQueue *L, datatype node_to_push); 71 datatype pop(SequenceQueue *L); 72 void showQueue(SequenceQueue *L); 73 74 int main(){ 75 /* 测试 */ 76 SequenceQueue *root; //指向一个通过createSequenceQueue函数创建的栈 77 root=createSequenceQueue(); 78 printf("isEmpty = %d ",isEmpty(root)); 79 printf("Length = %d ",getLength(root)); 80 push(root,'1'); 81 push(root,'2'); 82 push(root,'3'); 83 printf("isEmpty = %d ",isEmpty(root)); 84 printf("Length = %d ",getLength(root)); 85 showQueue(root); 86 putchar(' '); 87 printf("can continue to push? %d ",push(root,'4')); 88 printf("getTop = %c ",getTop(root)); 89 printf("pop = %c ",pop(root)); 90 printf("pop = %c ",pop(root)); 91 printf("isEmpty = %d ",isEmpty(root)); 92 printf("Length = %d ",getLength(root)); 93 push(root,'5'); 94 showQueue(root); 95 putchar(' '); 96 clear(root); 97 printf("isEmpty = %d ",isEmpty(root)); 98 printf("Length = %d ",getLength(root)); 99 100 return 0; 101 } 102 103 SequenceQueue *createSequenceQueue(void){ 104 SequenceQueue *tmp; 105 tmp=malloc(sizeof(SequenceQueue)); //void*类型指针能自动转为其他类型的指针 106 tmp->front=tmp->rear=0; //初始化队列的头尾指针 107 return tmp; 108 } 109 status isEmpty(SequenceQueue *L){ 110 if (L->front==L->rear) //front=rear表示队列是空的 111 return TRUE; 112 else 113 return FALSE; 114 } 115 void clear(SequenceQueue *L){ 116 L->front=L->rear=0; 117 } 118 datatype getTop(SequenceQueue *L){ 119 //返回队头元素的值 120 return L->data[L->front]; 121 } 122 int getLength(SequenceQueue *L){ 123 return (L->rear-L->front+MAXSIZE)%MAXSIZE; 124 } 125 status push(SequenceQueue *L, datatype node_to_push){ 126 //node_to_insert表示想要入队的元素 127 if ((L->rear+1)%MAXSIZE == L->front) return ERR; //队列已满 128 L->data[L->rear]=node_to_push; //将新元素入队 129 L->rear=(L->rear+1)%MAXSIZE; //指针rear后移 130 return OK; 131 } 132 datatype pop(SequenceQueue *L){ 133 datatype q; 134 if (isEmpty(L)) return ERR; //队列是空 135 q=L->data[L->front]; //将要出队的元素先赋值给临时变量s 136 L->front=(L->front+1)%MAXSIZE; //指针front后移 137 return q; //返回出队的元素的值 138 } 139 void showQueue(SequenceQueue *L){ 140 int i; 141 int total=getLength(L); 142 for (i=0; i<total; i++){ 143 printf("%c ",L->data[ (L->front+i)%MAXSIZE ]); 144 } 145 } 146 /* 147 队列的定义:只允许在一端进行插入,另一端进行删除的线性表,也是一种操作受限的线性表 148 一般,把允许插入的一端叫做队尾,允许删除的一端叫做队头 149 不含任何元素的队列就是空队 150 所以,队列又称先进先出(First in First out)的线性表 151 */ 152 /* 环境: Code::Blocks with GCC 5.1 */
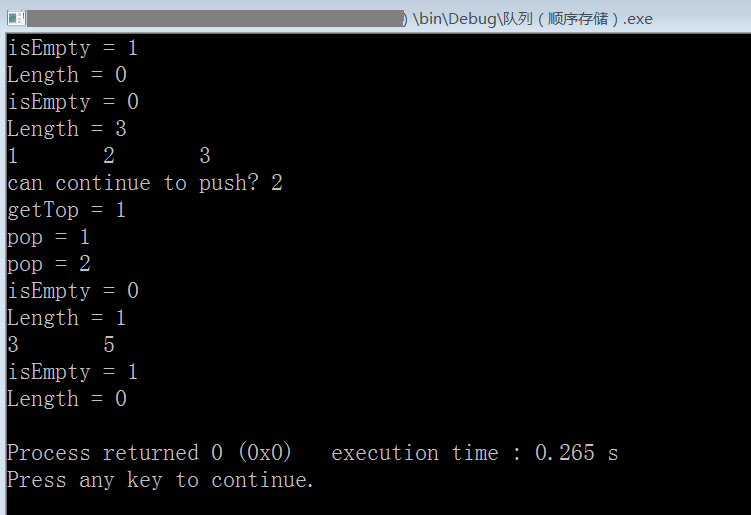
运行截图: