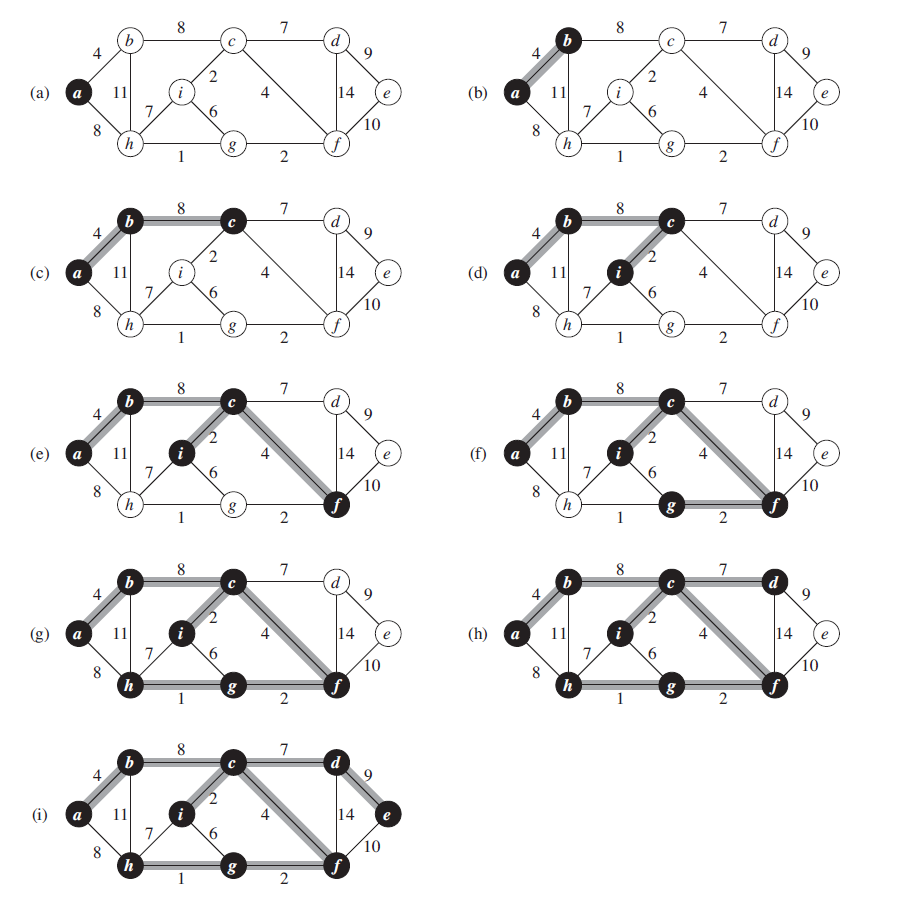
一个例子
在电子电路设计中,我们常常需要将多个组件的针脚连接在一起。要连接n个针脚,我们可以使用n-1根连线,每根连线连接两个针脚。显然,我们希望所使用的连线长度最短。
我们可以将上述问题用一个连通无向图G=(V,E)来表示,这里V是针脚的集合,E是针脚之间可能连接,每条边的权重代表两个针脚间连线的长度。
我们希望找到E的一个无环子集T(必为一棵树),既能够将所有针脚连接起来,又具有最小权重。我们称取该生成树的问题为最小生成树问题。
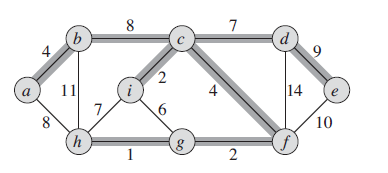
最小生成树可以用kruskal算法或prim算法求出。
可以形象的区分这两个算法:kruskal算法每次确定一条边,prim算法每次确定一个结点。
kruskal算法
伪代码
1 MST-KRUSKAL(G,w) 2 A=∅ 3 for each vertex v∈G.V 4 MAKE-SET(v) 5 sort the edges of G.E into nondecreasing order by weight w 6 for each edge(u,v)∈G.E,taken in nondecreasing order by weight 7 if FIND-SET(v)≠FIND-SET(v) 8 A=A∪{(u,v)} 9 UNION(v,u) 10 return A
集合A是最小生成树的边的集合,下面是代码的分析:
2-4 将集合A初始化为一个空集,并创建|V|棵树,每棵树仅包含一个结点
5 将图G的边按照权重递增的形式排序
6-9 按照权重从低到高对每条边进行检查。对于每条边(u,v)来说,检查端点u和端点v是否属于同一棵树:
1.如果是,该条边不能加入到森林里(否则将形成环路)
2.如果不是,则把这条边加入到集合A中,然后将两棵树中的结点进行合并
下面演示了kruskal算法的工作过程
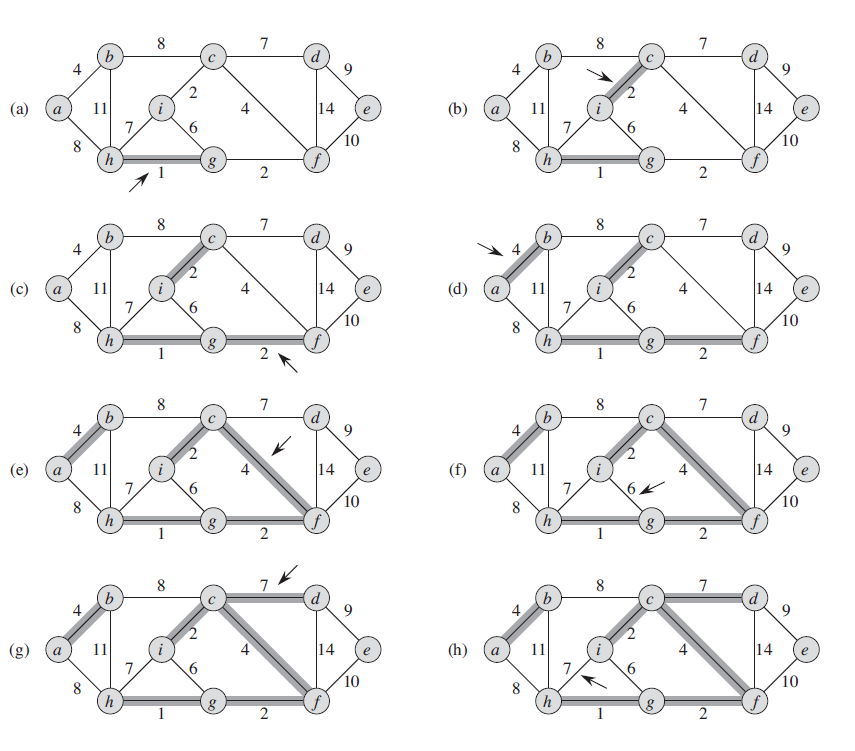
prim算法
伪代码
1 MST-PRIM(G,w,r) 2 for each u∈G.V 3 u:key=∞ 4 u:π=NIL 5 r:key=0 6 Q=G.V 7 while Q≠∅ 8 u=EXTRACT-MIN(Q) 9 for each v∈G.Adj[u] 10 if v∈Q and w(u,v)<v.key 11 v.π=u 12 v.key=w(u,v)
参数r是根结点,算法代码分析如下:
2-6 将每个结点的key值设置为∞,根结点r的key值设置为0。将每个结点的父结点设置为NIL。对最小优先队列Q进行初始化,使其包含图中所有的结点。
7-12 每次从Q中取出一个key值最小的(第一次是r)结点,然后更新该结点相邻结点的key值和父结点,直到Q为空。
下面演示了prim算法的过程。从根结点开始,每次找出一个距集合G-Q最小的结点加入。