稀疏矩阵有多种表示方法
- Compressed Row Storage
来自 <http://www.netlib.org/utk/people/JackDongarra/etemplates/node373.html>
矩阵向量乘法效率较低


这个比较好理解,
val: 非0的val按照行顺序排列
col_ind: 列索引 10这个val是第一列 -2对应第5 列 val(a_ij)对应col_ind(j)
如何表示出行信息?

Row_ptr(1) = 1
表示 val(1)的元素 在第一行
Row_ptr(2) = 3
表示val(3)的元素对应在第二行
最后row_ptr(-1) = numNonZeros + 1
Val(k) = a_ij
Row_ptr(i) <= k < row_ptr(i+1)
- Compressed Column Storage
来自 <http://www.netlib.org/utk/people/JackDongarra/etemplates/node374.html>
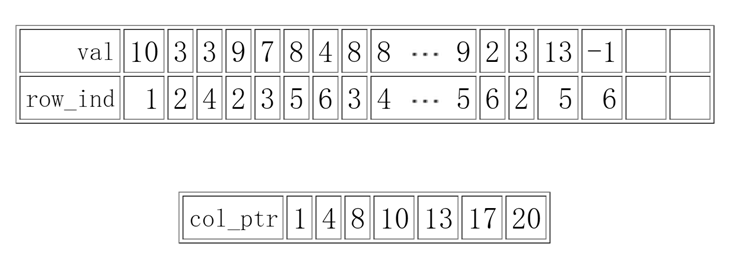
基本同上 当时是按照列顺序的
Col_ptr(2) = 4 则 val(4) = 9 表示9是第二列的开始
除了crs,ccs/csc外还有其它表示方法暂不介绍,thenao支持csr,ccs这两种方式。
- NumPy中的使用示例
这个是ccs/csc
- create using (data, ij) tuple:
>>> row = np.array([0, 0, 1, 2, 2, 2])
>>> col = np.array([0, 2, 2, 0, 1, 2])
>>> data = np.array([1, 2, 3, 4, 5, 6])
>>> mtx = sparse.csc_matrix((data, (row, col)), shape=(3, 3))
>>> mtx
<3x3 sparse matrix of type '<... 'numpy.int64'>'
with 6 stored elements in Compressed Sparse Column format>
>>> mtx.todense()
matrix([[1, 0, 2],
[0, 0, 3],
[4, 5, 6]]...)
>>> mtx.data
array([1, 4, 5, 2, 3, 6]...) #按照列顺序
>>> mtx.indices
array([0, 2, 2, 0, 1, 2], dtype=int32) #行号
>>> mtx.indptr
array([0, 2, 3, 6], dtype=int32) #第2列第一个非0 对应 mtx.data[2]=5
来自 <http://www.scipy-lectures.org/advanced/scipy_sparse/csc_matrix.html>
- create using (data, indices, indptr) tuple:
>>>
>>> data = np.array([1, 4, 5, 2, 3, 6])
>>> indices = np.array([0, 2, 2, 0, 1, 2])
>>> indptr = np.array([0, 2, 3, 6])
>>> mtx = sparse.csc_matrix((data, indices, indptr), shape=(3, 3))
>>> mtx.todense()
matrix([[1, 0, 2],
[0, 0, 3],
[4, 5, 6]])来自 <http://www.scipy-lectures.org/advanced/scipy_sparse/csc_matrix.html>