死亡之树

问题描述

小蛤为了迈向神犇之路，终于决定向一个超恶心的专题——树，发起攻击。他遇到了一个问题:给你一个n个点，m条无向边的图(保证没有重边)。如果这个图中的若干个点与连接它们的边组成的一棵树满足n个节点，k个叶子，则我们称这棵树为死亡之树。求这个图中有多少棵不同的死亡之树？
叶子的定义:度数为1的节点。
树相同的定义：如果两棵树所含节点的集合相同，且可以通过摆放，旋转转化为另一棵树的形状，我们称之为相同的树。

如     2    与   1-2-3    为一棵树
       /
       1 3

输入格式

第一行三个整数n,m,k代表n个点m条边,最终需要有k个叶子；
接下来m行每行两个整数a,b代表a点与b点有一条边。

输出格式

一个整数，代表有多少棵死亡之树。

样例输入

样例输出

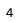
数据范围

题解

n<=10,于是这题跟状态压缩有关。

设f[i][j]表示当前树中已经加入的点的集合为i，叶子集合为j的方案数，其中i和j是点集的状态压缩。枚举没有在集合中的点和这个点会接在原有哪个节点的下面，然后对应转移。

考虑如何去重。由于不同形态的树被重复计算的次数不同，所以不能在最后计算完后再去重，需要一直保证f[i][j]没有重复。我们发现每一棵树最后加入的节点一定是一个叶子，所以可以通过叶子来区分。规定最后加入的叶子必须是节点编号最大（或者最小）的叶子，如果不满足则为非法转移，这样就能保证同一棵树只会被计算一次。复杂度O(4^N+N^2*3^N)。

#include <cstdio>
int n,m,K,a[15][15],b[1030],f[1030][1030],c[1030],p2[15],ans,cnt;
int main()
{
    int i,j,k,x,y,t,p;
    scanf("%d%d%d",&n,&m,&K);
    for (i=1;i<=m;i++)
      scanf("%d%d",&x,&y),
      a[x][y]=a[y][x]=1;
    for (i=1;i<=n;i++)
      b[1<<(i-1)]=i;
    for (p2[0]=i=1;i<=10;i++)
      p2[i]=1<<i;
    int nn=p2[n];
    for (i=1;i<=n;i++)
      for (j=1;j<=n;j++)
        c[p2[i-1]|p2[j-1]]=1;
    for (i=1;i<nn;i++)
      if (c[i])
      {
          for (j=1;j<=n;j++)
            if (i&p2[j-1])
              for (k=1;k<=n;k++)
                if (j!=k && a[j][k] && i&p2[k-1])
                  f[i][i]=1;
      }
      else 
      {
        for (t=i;t;t=i&(t-1))
          for (j=b[t&(-t)],k=1;k<=n;k++)
            if (j!=k && a[j][k] && (i&p2[k-1]) && !(t&p2[k-1]))
              f[i][t]+=f[i-p2[j-1]][t-p2[j-1]]+f[i-p2[j-1]][t-p2[j-1]+p2[k-1]];
      }
      for (i=1;i<nn;i++)
      {
          for (cnt=0,j=1;j<=n;j++)
            if (i&p2[j-1])
              cnt++;
          if (cnt==K) ans+=f[nn-1][i];
      }
    printf("%d",ans);
    return 0;
}