问题描述
小C终于被小X感动了,于是决定与他看电影,然而小X距离电影院非常远,现在假设每条道路需要花费小X的时间为1,由于有数以万计的好朋友沿路祝贺,导致小X在通过某些路不得不耗费1的时间来和他们聊天,尽管他希望尽早见到小C,所以他希望找到一条最快时间到达电影院的路。
一开始小X在1号点,共有N个点,M条路,电影院为T号点。
输入格式
第一行3个正整数,分别为n,m和t。
以下m行,每行3个数,表示连接的编号以及权值。
(注意,可能会有重边)
输出格式
一行一个数,表示1到t的最短路。
样例输入
10 12 6
3 9 2
6 9 2
6 2 1
3 1 1
1 9 2
2 8 2
7 10 1
7 2 1
10 0 1
8 1 1
1 5 2
3 7 2
样例输出
4
数据范围
对于 30%的数据:n≤10,m≤20;
对于 60%的数据:n≤1 000,m≤20 000;
对于 100%的数据:n≤5 000 000,m≤10 000 000。
题解
小X要从结点1到结点T(电影院),经过每条路的时间为1,有时候在路上遇到好朋友要额外花费1的时间聊天(即通过有好朋友的路需要的时间为2)
也就是说每条边的权值只能是1或2
看了一下数据范围好大。。。
SPFA是不是会TLE。。。
能用bfs的条件为每条边的权值都为1,本题我们可以把权值为2的边拆成两条权值为1的边
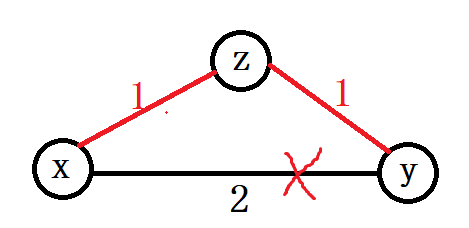
这样最多只会增加一倍的边,空间和时间都能接受
然后这个图每条边的权值都是1,用bfs最早到达的就是最短路
最后还要加上读入优化,数据很大没用读入优化还是会T
1 #include <cstdio> 2 #include <queue> 3 using namespace std; 4 int n,m,T,nn,fir[10000005],num,dis[10000005]; 5 struct node{ 6 int u,nex; 7 }g[40000005]; 8 queue<int> q; 9 bool vis[10000005]; 10 char ch; 11 int read() 12 { 13 int s=0; 14 ch=getchar(); 15 while (ch<'0' || ch>'9') 16 ch=getchar(); 17 while (ch>='0' && ch<='9') 18 s=s*10+ch-'0', 19 ch=getchar(); 20 return s; 21 } 22 void add(int x,int y) 23 { 24 g[++num].u=y; g[num].nex=fir[x]; fir[x]=num; 25 } 26 void bfs() 27 { 28 int u,k,v; 29 q.push(1); 30 vis[1]=1; 31 while (!q.empty()) 32 { 33 u=q.front(); 34 q.pop(); 35 for (k=fir[u];k;k=g[k].nex) 36 { 37 v=g[k].u; 38 if (vis[v]) continue; 39 vis[v]=1; 40 dis[v]=dis[u]+1; 41 if (v==T) 42 { 43 printf("%d\n",dis[v]); 44 return; 45 } 46 q.push(v); 47 } 48 } 49 } 50 int main() 51 { 52 //scanf("%d%d%d",&n,&m,&T); 53 n=read(); m=read(); T=read(); 54 int i,j,x,y,z; 55 nn=n; 56 for (i=1;i<=m;i++) 57 { 58 //scanf("%d%d%d",&x,&y,&z); 59 x=read(); y=read(); z=read(); 60 if (z==1) 61 add(x,y),add(y,x); 62 else 63 nn++, 64 add(x,nn),add(nn,x), 65 add(nn,y),add(y,nn); 66 } 67 bfs(); 68 return 0; 69 }