• 2018 Multi-University Training Contest 1

    1001:题面

    题意:给定一个数n，找出三个正整数x、y和z，满足：n=x+y+z,x|n,y|n,z|n。然后求xyz的最大值。

    题解:1=1/2+3/1+1/6=1/3+1/3+1/3=1/2+1/4+1/4 所以就三种

     1 #include <bits/stdc++.h>
 2 using namespace std;
 3 typedef long long LL;
 4 int main() {
 5     int T;
 6     scanf("%d", &T);
 7     while(T--) {
 8         LL n;
 9         scanf("%lld", &n);
10         if(n % 3 == 0) {
11             LL ans = n / 3;
12             ans = ans * ans * ans;
13             printf("%lld
", ans);
14         }
15         else if(n % 4 == 0) {
16             LL a = n / 4;
17             LL b = n / 2;
18             LL ans = a * a * b;
19             printf("%lld
", ans);
20         }
21         else puts("-1");
22     }
23     return 0;
24 }
    View Code

    1002:题面

    题意:给你n个包含’(‘与’)’的字符串,把这些字符串排序,求这些排序中,子序列是正规括号序列的最大长度。

    题解:对于2个字符串         IF s1 左少右多 vs s2 左多右少 THEN str2排在str1前面 

                                            IF s1 左多右少 vs s2 左少右多 THEN str1排在str2前面

    　　　　　　　　　　     IF s1 左少右多 vs s2 左少右多 THEN 左括号多的在前面

    　　　　　　　　　　　 ELSE 右括号少的在前面

     1 #include<bits/stdc++.h>
 2 using namespace std;
 3 #define N 100005
 4 #define lld long long
 5 struct Str
 6 {
 7     int l,r,add;
 8     bool operator < (const Str& s)const
 9     {
10         if(l<=r&&s.l>s.r)//左少右多  vs  左多右少
11         {
12             return false;
13         }
14         if(l>r&&s.l<=s.r)//左多右少  vs  左少右多
15         {
16             return true;
17         }
18         if(r>=l&&s.r>=s.l)//左少右多  vs  左少右多
19         {
20             return l>s.l;
21         }
22         return r<s.r;
23     }
24 }str[N];
25 char s[N];
26 int n,T;
27 int main()
28 {
29     scanf("%d",&T);
30     while (T--)
31     {
32         scanf("%d",&n);
33          for(int i=1;i<=n;i++)
34         {
35             scanf("%s",s);
36             str[i].l=str[i].r=str[i].add=0;
37             int len=strlen(s);
38             //count括号
39             for(int j=0;j<len;j++)
40             {
41                 if(s[j]=='(') str[i].l++;
42                 else
43                 {
44                     if(str[i].l>0) str[i].l--,str[i].add++;
45                     else str[i].r++;
46                 }
47             }
48         }
49         sort(str+1,str+1+n);
50         int ans=0;
51         int now=0;
52         for(int i=1;i<=n;i++)
53         {
54             str[i].r=min(str[i].r,now);
55             ans+=str[i].r+str[i].add;
56             now-=str[i].r;
57             now+=str[i].l;
58         }
59         cout<<ans*2<<endl;
60     }
61 }
    View Code

    1003:题面

    题意:给出3*N个点,让你输出N个三角形使得他们互不相交, 题目输出保证不会有三点共线。

    题解:因为不会有三点共线的情况,所以直接按x排序,直接输出即可

     1 #include <bits/stdc++.h>
 2 #define N 5005
 3 using namespace std;
 4 struct Node {
 5     int x,y,index;
 6 } node[N];
 7 bool cmp(Node a, Node b) 
 8 {
 9     if(a.x == b.x) return a.y < b.y;
10     return a.x < b.x;
11 }
12 int main() 
13 {
14     int T;
15     scanf("%d", &T);
16     while(T--) 
17     {
18         int n;
19         scanf("%d", &n);
20         for(int i = 1; i <= 3 * n; ++i) 
21         {
22             scanf("%d%d", &node[i].x, &node[i].y);
23             node[i].index = i;
24         }
25         sort(node + 1, node + 1 + 3 * n, cmp);
26         for(int i = 1; i <= 3 * n; i += 3) 
27             printf("%d %d %d
", node[i].index, node[i + 1].index, node[i + 2].index);
28     }
29     return 0;
30 }
    View Code

    1004:题面

    题意:构造一个长度为N的数组,有M个限制, 每个限制[L,R]区间,需要保证[L,R]区间内的数不能有重复,满足M个限制,且字典序最小的数组。

    题解:对于每个位置i维护一下他往前最远不能冲突的位置mp[i]，定义一个指针res,表示现在指针到的位置,维护下即可。

     1 #include<bits/stdc++.h>
 2 using namespace std;
 3 #define lld long long
 4 const int maxn = 1e5 + 5;
 5 int ans[maxn];
 6 struct Node 
 7 {
 8     int l, r;
 9     bool operator<(Node& a)
10     {
11         if (l == a.l)
12             return r > a.r;
13         return l < a.l;
14     }
15 } node[maxn];
16 int n,m,mp[maxn];
17 int main() 
18 {
19     int caseCnt;
20     scanf("%d", &caseCnt);
21     while (caseCnt--) 
22     {
23         scanf("%d%d", &n, &m);
24         for (int i = 1; i <= m; ++i) 
25             scanf("%d%d", &node[i].l, &node[i].r);
26         sort(node + 1, node + 1 + m);
27         memset(ans, -1, sizeof(ans));
28         memset(mp, 0, sizeof(mp));
29         for (int i = 1; i <= m; ++i) 
30         {
31             int pos = node[i].l - 1;
32             int ql = node[i].l, qr = node[i].r;
33             while (ql <= qr) 
34             {
35                 int mid = (ql + qr) >> 1;
36                 if (ans[mid] == -1) 
37                 {
38                     qr = mid - 1;
39                 }else 
40                 {
41                     ql = mid + 1;
42                     pos = mid;
43                 }
44             }
45             int res = 1;
46             for (int j = pos + 1; j <= node[i].r; ++j) 
47             {
48                 while (1) 
49                 {
50                     if (mp[res] < node[i].l) 
51                     {
52                         ans[j] = res;
53                         mp[res] = j;
54                         break;
55                     }
56                     res++;
57                 }
58             }
59         }
60         for (int i = 1; i <= n; ++i) 
61         {
62             if (ans[i] == -1) ans[i] = 1;
63             printf("%d%c", ans[i], (i == n ? '
' : ' '));
64         }
65     }
66     return 0;
67 }
    View Code

    1007:题面

    题意:

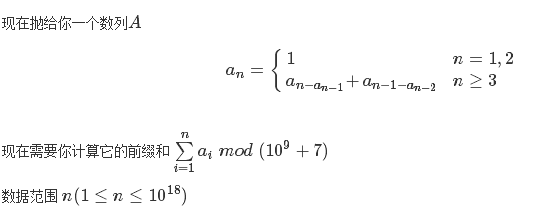
    题解:每个数出现的次数是log(lowbit(i))+1次,然后二分a[n]的值,对于同样的lowbit，构成了一个等差数列,再求和。

     1 #include<bits/stdc++.h>
 2 #define ll long long
 3 const ll mod=1e9+7;
 4 using namespace std;
 5 ll num[100],p[100];
 6 void init()
 7 {
 8     num[0]=p[0]=1;
 9     for (int i=1;i<=63;i++)
10     {
11         num[i]=2*num[i-1]+1;
12         p[i]=p[i-1]*2;
13     }
14 }
15 ll n,inv2=(mod+1)/2;
16 ll getsum(ll pos)
17 {
18     ll sum=0;
19     for (ll i=1;i<=pos;i*=2)
20     {
21         ll num=(pos-i)/(2*i);
22         ll Max=i+num*(2*i);
23         num=(num+1)%mod;
24         Max=(Max+i)%mod;
25         Max=Max*num%mod;
26         Max=Max*inv2%mod;
27         Max=Max*(__builtin_ctz(i)+1)%mod;//__builtin_ctz(x) 问x以多少个0结尾 这个数+1 就是log(nn&(-nn))/log(2)+1
28         sum=(sum+Max)%mod;
29     }
30     return (sum+1)%mod;
31 }
32 int main()
33 {
34     int t;
35     scanf("%d",&t);
36     init();
37     while (t--)
38     {
39         scanf("%lld",&n);
40         int nn=n;
41         ll pos=0;
42         n--;
43         if (!n)
44         {
45             printf("1
");
46             continue;
47         }
48         ll temp=n;
49         for (int i=62;i>=0;i--)
50             if (temp>=num[i])
51             {
52                 temp-=num[i];
53                 pos+=p[i];
54             }
55         ll sum1=getsum(pos);
56         if (temp)sum1=(sum1+temp%mod*(pos+1)%mod)%mod;
57         printf("%lld
",sum1);
58     }
59     return 0;
60 }
    View Code

    1008:题面

    题意:定义RMQ(A,l,r)为 序列A中,满足A[i] = max(A[l],A[l+1],...,A[r])的最小的i。如果对于任意(l,r)都满足RMQ(A,l,r)=RMQ(B,l,r)则为A和B是RMQ Similar。

    现在给你A序列，告诉你B序列的每个数都是0~1之间的实数，问满足与A是RMQ Similar的所有B序列中所有数之和的期望。

    题解:首先要了解笛卡尔树这个东西，然后可以发现，如果A和B是RMQ Similar，则A和B的笛卡尔树同构。考虑B中的每个数是0~1之间的实数，因此我们可以认为出现相同数字的概率为0，可以假设B是每个数都不相同排列。设A的笛卡尔树每个子树的大小为sz[u]，则任一B排列与A同构的概率是prod_{1}^{n} frac{1}{sz[i]}，因为B中每个数满足均匀分布，因此期望值为frac{1}{2}，和的期望为frac{n}{2}，因此满足与A同构的B中所有数之和的期望为frac{n}{2prod_{1}^{n}sz[i]}

     1 #include<bits/stdc++.h>
 2 using namespace std;
 3 typedef long long LL;
 4 #define N 1000005
 5 const int mod = 1e9 + 7;
 6 const int INF = 0x3f3f3f3f;
 7 struct node {
 8     int val,sz,l, r, pre;
 9 }t[N];
10 stack<int>st;
11 void init (int n)
12 {
13     for (int i = 0; i <= n; i++) t[i].l = t[i].r = t[i].pre = t[i].sz = 0;
14     t[0].val = INF;
15     while (!st.empty() ) st.pop();
16     st.push (0);
17 }
18 void build (int n)
19 { //从右端插入
20     for (int i = 1; i <= n; i++)
21     {
22         while (!st.empty() && t[st.top()].val < t[i].val) st.pop();
23         int pre = st.top();
24         t[i].pre = pre;
25         t[i].l = t[pre].r;
26         t[t[pre].r].pre = i;
27         t[pre].r = i;
28         st.push (i);
29     }
30 }
31 void dfs (int u)
32 {
33     if (u == 0) return;
34     t[u].sz = 1;
35     dfs (t[u].l);
36     dfs (t[u].r);
37     t[u].sz += t[t[u].l].sz + t[t[u].r].sz;
38 }
39 int T,n;
40 LL inv[N];
41 int main()
42 {
43     cin >> T;
44     inv[1] = 1;
45     for (int i = 2; i < N; i++) inv[i] = inv[mod % i] * (mod - mod / i) % mod;
46     while (T--)
47     {
48         scanf ("%d", &n);
49         init(n);
50         for (int i = 1; i <= n; i++) scanf ("%d", &t[i].val);
51         build(n);
52         dfs(t[0].r);
53         LL ans = n * inv[2] % mod;
54         for (int i = 1; i <= n; i++) ans = ans * inv[t[i].sz] % mod;
55         printf ("%lld
", ans);
56     }
57     return 0;
58 }
    View Code

    1011:题面

    题意:给出一个标准时间UTF+8,给出一个当前时间和时区,计算当前标准时间。

    题解:转换为小数,直接模拟即可

     1 #include<bits/stdc++.h>
 2 using namespace std;
 3 int T,x,y;
 4 char a,b,c,d;
 5 char s[5];
 6 double ct,tt;
 7 int main()
 8 {
 9     scanf("%d
",&T);
10     while (T--)
11     {
12         scanf("%d%d",&x,&y);
13         scanf("%c%c%c%c%c%s",&c,&c,&c,&c,&c,s);
14         if (strlen(s)==1) 
15         {
16             ct=s[0]-'0';
17             tt=0;
18         }else
19         { 
20             if (s[1]=='.')
21             {
22                 ct=s[0]-'0';
23                 tt=(s[2]-'0')*0.1;
24             }else 
25             {        
26                 if (strlen(s)>=2) ct=(s[0]-'0')*10+(s[1]-'0'),tt=0;
27                 if (s[2]=='.') tt=(s[3]-'0')*0.1;
28             }
29         }
30         if (c=='-') 
31         {
32             ct=ct*(-1);
33             tt=tt*(-1);
34         }
35         ct=ct-8;
36         x=x+(int)ct;
37         int yy=60*tt;
38         y=y+yy;
39 
40         if (y>=60)
41         {
42             x+=1;
43             y-=60;
44         }
45         if (y<0)
46         {
47             x-=1;
48             y+=60;
49         }
50         if (x>=24) x-=24;
51         if (x<0) x+=24;
52         if (x<10) printf("0"); printf("%d:",x);
53         if (y<10) printf("0");printf("%d
",y);
54         scanf("
");
55     }
56 }
    View Code
    Anderyi!
  • 相关阅读:
    C# 连接数据库
    MySQL数据类型char与varchar中数字代表的究竟是字节数还是字符数？
    group by与avg(),max(),min(),sum()函数的关系
    MySQL内连接、外连接、交叉连接
    Mysql 插入中文错误：Incorrect string value: 'xE7xA8x8BxE5xBAx8F...' for column 'course' at row 1
    session和token
    session和cookies
    sessionid如何产生？由谁产生？保存在哪里？
    跨域，你需要知道的全在这里
    匈牙利算法模板
  • 原文地址：https://www.cnblogs.com/qywhy/p/9673964.html
Copyright © 2020-2023  润新知