三分法

二分法适用于在单调函数上通过不断逼近的方式寻找答案，一般用于“判定性问题”

而三分法则用于凹凸函数，寻找其凹点和凸点

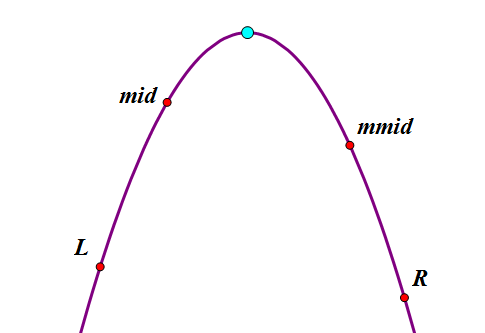
例如上图的函数是个凸函数，蓝色点便是凸点

三分的基本步骤就是先将 [ L, R ] 分为 [ L, mid ] && [ mid, R ] 中点为 mid

然后将 [ mid, R ] 再二分一次分为 [ mid, mmid ] && [ mmid, R ]

如果函数值 f(mid) > f(mmid) 那么 mmid 一定在凸点的右边，所以执行 R = mmid

否则反之 L = mid，直到找到凸点

凹点的查找结论就和凸点相反了

///找凸点
int Three_Devide(int L,int R)
{
    while(L < R-1){
        int mid  = (L + R)/2;
        int mmid = (mid + R)/2;
        if( f(mid) > f(mmid) )  R = mmid;
        else  L = mid;
    }
    return f(L) > f(R) ? L : R;
}

double Three_Devide(double low,double up)
{
    double m1,m2;
    while(up-low>=eps){
        m1=low+(up-low)/3;
        m2=up-(up-low)/3;
        if(f(m1)<=f(m2)) low=m1;
        else up=m2;
    }
    return (m1+m2)/2;
}

///找凹点
int Three_Devide(int L,int R)
{
    while(L < R-1){
        int mid  = (L + R)/2;
        int mmid = (mid + R)/2;
        if( f(mid) > f(mmid) )  L = mmid;
        else  R = mid;
    }
    return f(L) > f(R) ? R : L;
}

double Three_Devide(double low,double up)
{
    double m1,m2;
    while(up-low>=eps)
    {
        m1=low+(up-low)/3;
        m2=up-(up-low)/3;
        if(f(m1)<=f(m2))
            up=m2;
        else
            low=m1;
    }
    return (m1+m2)/2;
}