题目描述
某大学有N个职员,编号为1~N。他们之间有从属关系,也就是说他们的关系就像一棵以校长为根的树,父结点就是子结点的直接上司。现在有个周年庆宴会,宴会每邀请来一个职员都会增加一定的快乐指数Ri,但是呢,如果某个职员的上司来参加舞会了,那么这个职员就无论如何也不肯来参加舞会了。所以,请你编程计算,邀请哪些职员可以使快乐指数最大,求最大的快乐指数。
输入输出格式
输入格式:
第一行一个整数N。(1<=N<=6000)
接下来N行,第i+1行表示i号职员的快乐指数Ri。(-128<=Ri<=127)
接下来N-1行,每行输入一对整数L,K。表示K是L的直接上司。
最后一行输入0 0
输出格式:
输出最大的快乐指数。
输入样例 输出样例
7 5
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5
0 0
今天真是幸运的一天,新学的树状DP一下A了,可以说是我学DP以来最稳的一次。可能是之前在B站上看了“正月点灯笼” 的DP教学,加上今天Xing学长的悉心教导,做这道题时行云流水。
解析:
树形DP这么命名,正是因为DP关系是呈树形的,依照样例,如图:
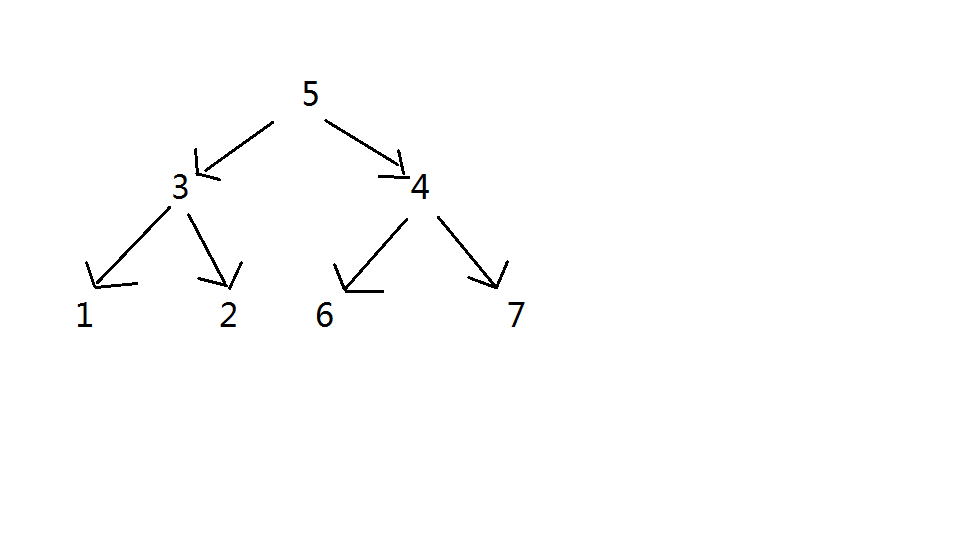
- 用 indu[ ] 存每个节点的入度情况,然后找到入度为 0 的点(也就是根节点),标记上,作为dfs的起始
- 用 hap[ ] 记录每个节点的开心值
- 开一个 f[MX][2] , f[i][0] 表示不选 i 的最优情况,f[i][1] 表示选 i 的最优情况
- 深搜下去,每搜一个节点,先把 f[from][1] 赋值为hap[from]
- 如果你选了上司,直系下属就不能选,但可以加上直系下属不选的最优 f[to][0] 来使得f[from][1] 最优
- 如果你不选上司,直系下属都可以选,但你选了不一定比不选好,所以 f[from][0]+=max(f[to][1],f[to][0])
代码^-^
#include<stdio.h> #include<algorithm> using namespace std; int f[6001][2],hap[6001],first[6001],indu[6001]; struct Edge{ int to,next; }edge[6001]; int cnt,st; void add(int to,int from) { edge[++cnt].to=to; edge[cnt].next=first[from]; first[from]=cnt; indu[to]++; } void dfs(int from) { f[from][1]=hap[from]; for(int i=first[from];i;i=edge[i].next) { int to=edge[i].to; dfs(to); f[from][1]+=f[to][0]; f[from][0]+=max(f[to][1],f[to][0]); } } int main() { int n; scanf("%d",&n); for(int i=1;i<=n;++i) scanf("%d",&hap[i]); int down,up; while(scanf("%d%d",&down,&up)!=EOF) { if(down==0 && up==0) break; add(down,up); } for(int i=1;i<=n;++i) if(indu[i]==0) { st=i; break; } dfs(st); printf("%d",max(f[st][1],f[st][0])); return 0; }