顺序表上基本操作的实现

线性表在采用不同的存储结构时，它的描述方法是不一样的，那么它的基本操作实现方法也截然不同。下面来看线性表在顺序存储下，也就是顺序表的每一个基本操作的具体实现方法以及编写方法。

插入操作

还是上一个例子，一群朋友去吃火锅。此时有一个女生过来了，她叫小红。小红是小绿的女朋友，当然想和小绿坐在一起，但是小绿旁边是没有空位置的。所以小绿麻烦他旁边的朋友小黄和小黑依次移动了一个位置。这样就空出了一个位置，小红就可以过来坐下了。这样就完成了一个类似顺序表插入的过程。

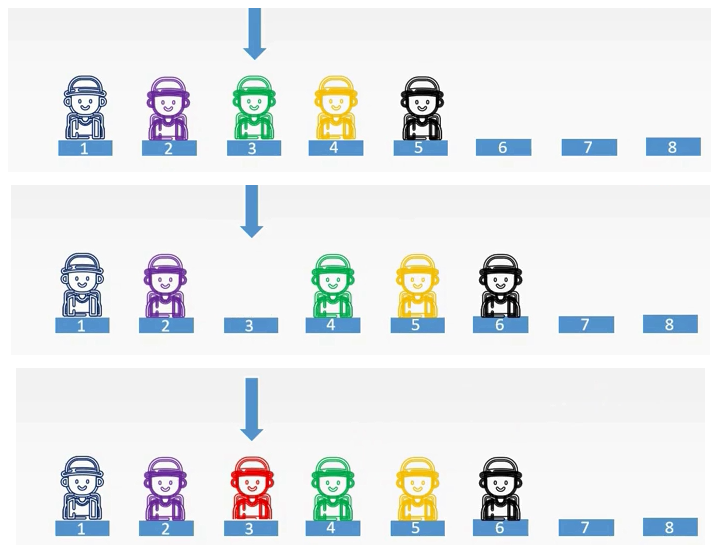
代码实现

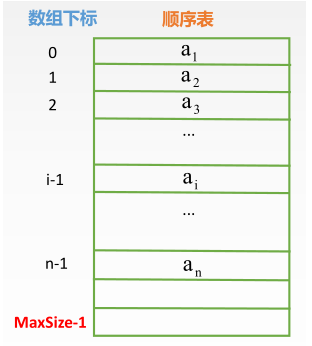
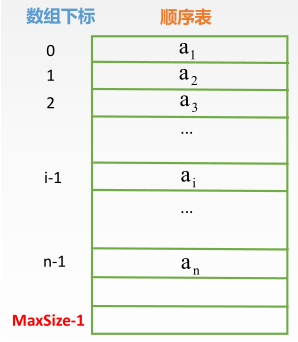
知道了顺序表插入的大致过程，来看它用程序语言是如何编写的。首先画出了一个顺序表

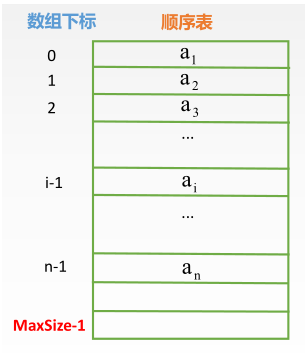
其中数据元素是连续存放的。接着标出了存放该顺序表数据元素的数组下标。注意一下，数组下标是从 0 开始的，而顺序表的元素标号是从 1 开始的。接着用 C++ 写出了该插入操作的函数体：

bool ListInsert(SqList &L, int i, ElemType e) {
    if(i<1 || i>L.length+1)
        return false;
    if(L.length >= MaxSize)
        return false;
    for(int j=L.length; j>=i; j--)
        L.data[j] = L.data[j-1];
    L.data[i-1] = e;
    L.length++;
    return true;
}

它的返回值类型是一个布尔类型，表示如果插入成功会返回一个 True ，插入失败会返回一个 False。它有三个参数，分别是一个引用类型的顺序表 L，这里为什么用引用类型？因为在函数体内部进行操作，其实是作用一个局部变量上的，不会真正作用到这个参数上，如果不用引用类型，是不能把插入操作真正作用到传入的顺序表上的。接着是一个整型变量 i，它表示的是插入的位置，要注意在采用插入操作时，往往是前插法，这是一个默认规定。还有一点要注意的就是，i 对应的是顺序表的表号而非数组的下标。最后一个参数是所插入的数据元素 e。

首先第一个条件 i<1 || i>L.length+1 ，顺序表的元素标号是从 1 开始的，i 表示的是插入的位置，如果插入的位置是 0 或者更小，又或者比 L.length+1 还大，都是不合法的。第二个条件判断的是插入的数组是否有足够空间去插入，因为数组不可以增加容量，一旦满了就没用新的空间去提供插入了。循环语句中申请了变量 j 初始化为顺序表的长度，j 进行减一操作，一直到 j=i 的时候中止循环。循环体中 L.data[j] = L.data[j-1] 的意思就是把每一个数据元素向后移了一位，一直移动到 a_i 移动到原先 a_i+1 的位置。 执行完了所有的循环，空出了一个位置用于插入，L.data[i-1] = e 就是把要插入的元素放到该位置。注意，在 i 的位置，元素对应的下标是 i-1。最后将顺序表的长度加一。

时间复杂度

再来看一下这个程序的时间复杂度，当循环次数最少时，它就是最好的时间复杂度，什么时候循环次数最少呢？发现当在顺序表的尾部，也就是 L.length+1 的时候，这时候不用进行元素的移动，它的循环次数是 0，所以它的最好时间复杂度是 O(1) ，因为它的语句频度是常数级别的。

接着来看平均时间复杂度，平均时间复杂度是在所有情况等概率的情况下，计算它的期望。这里的等概率，一定是合法的情况。所以 i 一共有 n+1 个合法位置，n 个数据元素，加上第 n 个数据元素之后的那个位置，都可以进行插入。所以每一个插入等概率的情况下，它的概率是：

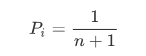
接着根据概率的知识，可以用每一个位置的概率乘以它循环的次数，它是从尾部一直循环到 i ，所以循环了 n-i+1 次，根据等差数列求和公式可以计算：

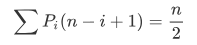
计算结果与 n 同阶无穷大，所以它的平均时间复杂度为 O(n) 。

最坏就是循环次数最多，即每一个数据元素都要向后移动一位，也就是插入在第一个位置时是最坏的情况，所以要循环 n 次，所以最坏情况下的时间复杂度是 O(n) 。

删除操作

还是一群小伙伴在等候区等待吃火锅，这时小绿被他的女朋友叫回去一起学习数据结构，那么小绿要走了，小绿走了之后就空出了一个位置。在等候区中间是不可以有空的位置的，所以说小黄和小黑两个人会依次向前移一位。

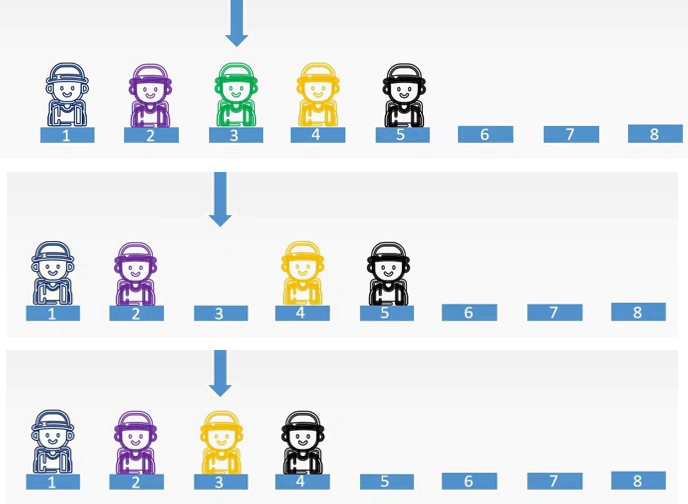
这也就是删除操作的大致过程。接着来看它的代码实现。

代码实现

bool ListDelete(SqList &L, int i, ElemType &e) {
    if(i<1 || i>L.length)
        return false;
    e = L.data[i-1]
    for(int j=i; j<L.length; j++)
        L.data[j-1] = L.data[j];
    L.length--;
    return true;
}

函数的返回值依旧是一个布尔类型。它有三个参数，分别是一个引用类型的顺序表 L，一个整型变量 i 表示删除的位置，一个引用类型的数据元素 e ，这里使用引用类型也是因为在函数体内部进行操作，是作用在一个局部变量上的，不会真正作用到这个参数 e 上，所以说使用引用类型来将所删除的这个数据元素真正的返回到函数外部。

第一个条件是判断删除的位置是否合法。接着 e = L.data[i-1] 是在保存要删除的数据元素，将 i 位置的数据元素，对应下标 i-1，赋值给 e 。然后循环从 i 开始，每次进行加一操作，一直循环到 L.length-1 为止，也就是从 i 一直循环到 n-1，将 a_i 赋值给 a_i+1 ，也就是将数组下标为 i 的赋值给 i-1 的，这样就将 a_i 之后的所有数据元素都向前移了一位。接着将顺序表的长度减一。

时间复杂度

最好的时间复杂度是删除最后一个元素，它的最好时间复杂度是 O(1) 。

所有合法的删除位置有 n 个，因为有 n 个数据元素。所以每一个合法位置的概率都是 1/n ，它的循环次数是从 i 循环到 L.length-1 ，所以是 n-i 次，所以它的期望是 (n-1)/2 ，它与 n 同阶无穷大，所以它的平均时间复杂度为 O(n) 。

删除第一个数据元素循环的次数最多，此时需要循环 n-1 次，与 n 同阶无穷大，因此最坏时间复杂度为 O(n) 。

按值查找

需要找到等候区的小绿，等候区是这样依次坐下的。于是依次进行查找，从第一个位置开始，一直找到第三个位置，发现他是小绿。

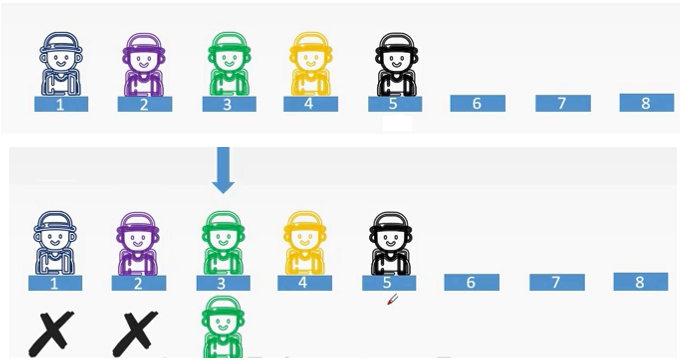
这样的查找过程，就与按值查找的函数十分相似。

代码实现

int Locate(SqList &L, ElemType e) {
    int i;
    for(i=0; i<L.length; i++)
        if(L.data[i] == e)
            return i+1;
    return 0;
}

这个函数的返回值是一个整型变量，它表示返回的是一个顺序表的下标。两个参数分别是查找的顺序表以及查找的值。所有对输入参数进行修改的操作，都使用引用类型。所有进行查找的操作都不会使用引用类型。

首先是一个整型变量 i ，它用来存放最终的输出结果。接着是一个循环，变量 i 从下标 0，也就是第一个元素开始，每一次循环进行加一操作，一直循环到 L.length-1 ，也就是下标 n-1 的位置，一共执行了 n 次。循环体的内容是一个判断语句，判断此时数据元素是否为要找的那个元素，如果相等返回当前顺序表的下标，也就是 i+1。最后 return 0 表示循环结束了，还没有找到对应的这个值的位置，那么就说明顺序表当中是没有该值的，此时就返回一个 return 0 表示查找失败。

时间复杂度

最好的时间复杂度依旧是循环的次数最少，也就是第一个数据元素就是要找的那个值，所以最好的时间复杂度为 O(1) 。

一共有 n 个元素，查找概率是 1/n ，查找次数是 n-i 次，它的期望是 (n+1)/2 ，它与 n 同阶无穷大，所以它的平均时间复杂度为 O(n) 。

最后一个元素被找到是最坏的情况，循环了 n 次，因此最坏时间复杂度为 O(n) 。

总结