1 基本函数确立
1.1 回归的形式—标记/label
-
回归模型可预测连续值。例如,回归模型做出的预测可回答如下问题:
-
加利福尼亚州一栋房产的价值是多少?
-
用户点击此广告的概率是多少?
-
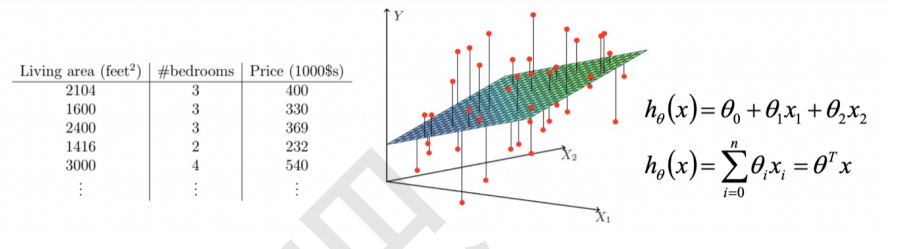
- 例如,下表显示了从包含加利福尼亚州房价信息的数据集中抽取的 5 个有标签样本:

1.2 代码实验
import numpy as np import matplotlib.pyplot as plt from sklearn.linear_model import LinearRegression # 100个数,1列,rand表示均匀分布,在0~1之间 X = 2 * np.random.rand(100, 1) # print(X) # y表示认为设置真实的一列Y,np.random.randn(100,1)表示error,randn表示标准正太分布 y = 3 + 6 * X + np.random.randn(100, 1) # print(y) lin_reg = LinearRegression() lin_reg.fit(X, y) print("θ = ",lin_reg.coef_) print("---------------------------------") print("截距项 = ",lin_reg.intercept_) print("---------------------------------") X_new = np.array([[0], [2]]) y_predict = lin_reg.predict(X_new) print(y_predict) θ = [[6.394389]] --------------------------------- 截距项 = [2.63594646] --------------------------------- [[ 2.63594646] [15.42472446]]
# 可视化 plt.plot(X_new, y_predict, 'r-') plt.plot(X, y, 'k.') plt.axis([0, 2, 0, 15]) plt.show()
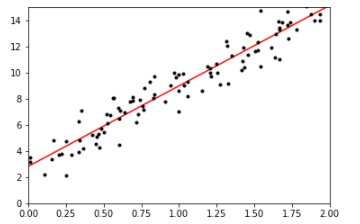
- 机器学习的所有算法,系统都是学的是参数theta;咱们不仅要代码实现出来,在学习算法的时候呀,咱们也要进行“参数估计”
2 目标函数如何建立
2.1 叙谈基本函数
- 基本函数:人为假设的,让(x,y)这样的符合y=f(x;θ)的假设函数
# 可视化 plt.plot(X_new, y_predict, 'r-') plt.plot(X, y, 'k.') plt.axis([0, 2, 0, 15]) plt.show()
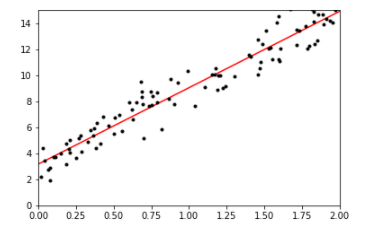
- 目标函数与最优方法


2.2 目标函数推导
2.2.1 矩阵推导

2.2.2 目标函数推导
- 试推导一下当theta多少时,J(theta)最小呢?

3 确立最优函数
最优方法/工具:梯度下降算法

4.案例:广告与多媒体之间的预测
#!/usr/bin/python # -*- coding:utf-8 -*- import csv import numpy as np import matplotlib.pyplot as plt import matplotlib as mpl import pandas as pd from sklearn.model_selection import train_test_split from sklearn.linear_model import LinearRegression if __name__ == "__main__": path = './data/Advertising.csv' # pandas读入 # 一、加载数据集 data = pd.read_csv(path) # TV、Radio、Newspaper、Sales x = data[['TV', 'Radio', 'Newspaper']] # 建立特征矩阵 200 * 4 y = data['Sales'] # 建立 标签矩阵 200 * 1 print(x) print(y) TV Radio Newspaper 0 230.1 37.8 69.2 1 44.5 39.3 45.1 2 17.2 45.9 69.3 3 151.5 41.3 58.5 4 180.8 10.8 58.4 .. ... ... ... 195 38.2 3.7 13.8 196 94.2 4.9 8.1 197 177.0 9.3 6.4 198 283.6 42.0 66.2 199 232.1 8.6 8.7 [200 rows x 3 columns] 0 22.1 1 10.4 2 9.3 3 18.5 4 12.9 ... 195 7.6 196 9.7 197 12.8 198 25.5 199 13.4 Name: Sales, Length: 200, dtype: float64
# 设置字符集,防止中文乱码 # mpl.rcParams["font.sans-serif"] = [u'simHei'] #Win自带的字体 plt.rcParams['font.sans-serif'] = ['Arial Unicode MS'] #Mac自带的字体 mpl.rcParams["axes.unicode_minus"] = False
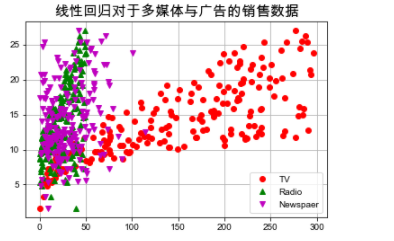
# 绘制1 plt.plot(data['TV'], y, 'ro', label='TV') plt.plot(data['Radio'], y, 'g^', label='Radio') plt.plot(data['Newspaper'], y, 'mv', label='Newspaer') plt.title("线性回归对于多媒体与广告的销售数据", fontsize=16) plt.legend(loc='lower right') plt.grid() plt.show()
# 绘制2 plt.figure(figsize=(9,12)) plt.subplot(311) plt.plot(data['TV'], y, 'ro') plt.title('TV') plt.grid() plt.subplot(312) plt.plot(data['Radio'], y, 'g^') plt.title('Radio') plt.grid() plt.subplot(313) plt.plot(data['Newspaper'], y, 'b*') plt.title('Newspaper') plt.grid() plt.tight_layout() plt.show()

# 二、分割数据集 x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=1) # print(x_train, y_train) # 三、选择/建立模型 linreg = LinearRegression() # 四、训练模型 model = linreg.fit(x_train, y_train) print("linereg的theta = ",linreg.coef_) print() print("linreg的截距项 = " ,linreg.intercept_)
linereg的theta = [0.04656457 0.17915812 0.00345046] linreg的截距项 = 2.8769666223179318
# 五、验证模型 y_hat = linreg.predict(np.array(x_test)) mse = np.average((y_hat - np.array(y_test)) ** 2) # Mean Squared Error rmse = np.sqrt(mse) # Root Mean Squared Error print("MSE = " , mse) print() print(mse, rmse)
MSE = 1.9730456202283366 1.9730456202283366 1.4046514230328948
from sklearn.metrics import r2_score r2_score(y_test, y_hat)
0.9156213613792232
t = np.arange(len(x_test)) plt.plot(t, y_test, 'r-', linewidth=2, label='Test') plt.plot(t, y_hat, 'g-', linewidth=2, label='Predict') plt.title("线性回归对于多媒体与广告的销售数据", fontsize=16) plt.legend(loc='upper right') plt.grid() plt.show()

- 线性回归的定义,是利用最小二乘函数对一个或多个自变量之间关系进行建模的方法
- 多元回归的分析思路(参数估计)都与一元回归完全相同
5、总结
5.1 什么是线性回归
线性:两个变量之间的关系是一次函数关系的——图象是直线,叫做线性。 非线性:两个变量之间的关系不是一次函数关系的——图象不是直线,叫做非线性。 回归:人们在测量事物的时候因为客观条件所限,求得的都是测量值,而不是事物真实的值,为了能够得到真实值,无限次的进行测量,最后通过这些测量数据计算回归到真实值,这就是回归的由来。
5.2 能够解决什么样的问题
对大量的观测数据进行处理,从而得到比较符合事物内部规律的数学表达式。也就是说寻找到数据与数据之间的规律所在,从而就可以模拟出结果,也就是对结果进行预测。解决的就是通过已知的数据得到未知的结果。例如:对房价的预测、判断信用评价、电影票房预估等。
5.3 过拟合、欠拟合如何解决
使用正则化项,也就是给loss function加上一个参数项,正则化项有L1正则化、L2正则化、ElasticNet。加入这个正则化项好处:
控制参数幅度,不让模型“无法无天”。 限制参数搜索空间 解决欠拟合与过拟合的问题。