列出.net中数据结构对应的技术点：
下面笔记参考书籍《数据结构实践》C#李春葆版，但是大佬说这本书有不少坑，所以要对照C语言严蔚敏版的《数据结构》，待研究研究
参考：
数据结构是什么：
数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下，精心选择的数据结构可以带来更高的运行或者存储效率。数据结构往往同高效的检索算法和索引技术有关。
逻辑结构分类：
- 集合结构：是一种松散的逻辑结构。例如List<>
- 线性结构：元素之间存在一对一关系常见类型有: 数组,链表,队列,栈,它们之间在操作上有所区别.例如:链表可在任意位置插入或删除元素,而队列在队尾插入元素,队头删除元素,栈只能在栈顶进行插入,删除操作。例如通讯录、成绩单、花名册
- 树形结构：元素之间存在一对多关系,常见类型有:树(有许多特例:二叉树、平衡二叉树、查找树等)。例如目录、家谱、电子字典
- 图状结构：素之间存在多对多关系,图形结构中每个结点的前驱结点数和后续结点多个数可以任意。例如交通线路、通信网络
存储结构(物理结构)分类：存储结构是将数据及其逻辑关系存储到计算机内存中，常用的存储结构类型有：
- 顺序存储：按照顺序来存储
- 链式存储：随机存储，终点间的逻辑关系通过指针来表示。例如：单链表、双链表
- 索引存储：在存储数据元素时简历附加索引表
- 哈希存储：根据节点的关键字通过哈希(或散列)函数直接计算出一个只，并将这个值作为该节点的存储地址
常用数据结构有：
- 链表 ( Linked List [lɪŋkt lɪst] )
- 栈 (Stack [stæk] ) 和队列 (Queue [kjuː] )
- 串
- 数组 (Array [əˈreɪ] ) 和广义表
- 树 (Tree [triː] ) 和二叉树
- 图 (Graph [ɡræf] )
线性表：
线性表示具有相同特性的数据元素的一个优先序列。包含的数据结构有：顺序表、链表
链表：
是一种常见的基础数据结构，是一种线性表，但是并不会按线性的顺序存储数据，而是在每一个节点里存到下一个节点的指针(Pointer)。由于不必须按顺序存储，链表在插入的时候可以达到O(1)的复杂度，比另一种线性表顺序表快得多，但是查找一个节点或者访问特定编号的节点则需要O(n)的时间，而顺序表相应的时间复杂度分别是O(logn)和O(1)。
单链表：链表中最简单的一种是单向链表，它包含两个域，一个信息域和一个指针域。这个链接指向列表中的下一个节点，而最后一个节点则指向一个空值。
/// <summary> /// //定义单链表结点类 /// </summary> public class LinkList { /// <summary> /// //存放数据元素 /// </summary> public string data; /// <summary> /// //指向下一个结点的字段：核心是调用自己，来创建下一个结点地址 /// </summary> public LinkList next; }; /// <summary> /// //单链表头结点 /// </summary> public LinkList head = new LinkList(); /// <summary> /// //尾插法建立单链表 /// </summary> /// <param name="split"></param> public void CreateListR(string[] split) { LinkList s, r; //不实例化 int i; //赋值指针：head是已经new过的了，声明r直接指向head，更改r时head也会跟着改变,因为r指向head r = head; //r始终指向尾结点,开始时指向头结点 for (i = 0; i < split.Length; i++) //循环建立数据结点 { //要先填写第二层的data才能第一层的next地址，否则一开始就给第一层data，因为第二层没有数据，第一层的next无法获取 s = new LinkList(); //每层都新new一个单链表结点类 s.data = split[i]; //创建数据结点s，从 split[i]数组中取值到s.data r.next = s; //将s结点插入r结点之后 r = s; //r指针向s } r.next = null; //将尾结点的next字段置为null }
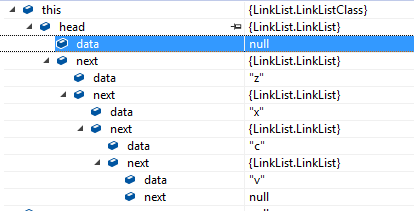
输入：z,x,c,v 测试单链表
第一层不用看，从第二层开始看跟踪结构发现每一层都是一个结点data和下个结点的引用地址next
双链表：一种更复杂的链表是“双向链表”或“双面链表”。每个节点有两个连接：一个指向前一个节点，（当此“连接”为第一个“连接”时，指向空值或者空列表）；而另一个指向下一个节点，（当此“连接”为最后一个“连接”时，指向空值或者空列表）
/// <summary> /// //双链表结点类 /// </summary> public class DLinkList { public string data; //存放数据元素 public DLinkList prior; //指向前一个结点的字段 public DLinkList next; //指向下一个结点的字段 }; public DLinkList dhead = new DLinkList(); //双链表头结点 /// <summary> /// //尾插法建立双链表 /// </summary> /// <param name="split"></param> public void CreateListR(string[] split) { DLinkList s, r; int i; r = dhead; //r始终指向尾结点,开始时指向头结点 for (i = 0; i < split.Length; i++) //循环建立数据结点 { s = new DLinkList(); s.data = split[i]; //创建数据结点s r.next = s; //将s结点插入r结点之后 s.prior = r; r = s; } r.next = null; //尾结点的next字段置为null }
输入A,B,C测试双链表，跟踪：
第一层不用看
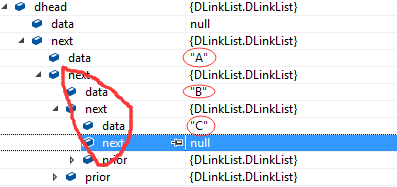
从第二层开始看，看next指向后一个结点数据，从A开始，后面有B，B后面有C：
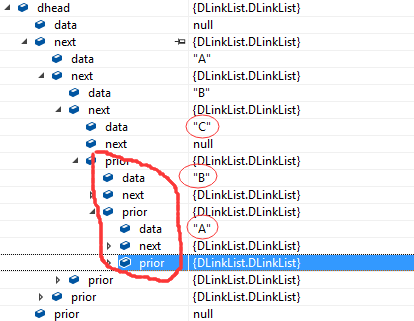
看prior指向前一个结点数据，从C开始看前面有B，B前面有A：
循环链表：
在一个 循环链表中, 首节点和末节点被连接在一起。这种方式在单向和双向链表中皆可实现。要转换一个循环链表，你开始于任意一个节点然后沿着列表的任一方向直到返回开始的节点。再来看另一种方法，循环链表可以被视为“无头无尾”。这种列表很利于节约数据存储缓存， 假定你在一个列表中有一个对象并且希望所有其他对象迭代在一个非特殊的排列下。指向整个列表的指针可以被称作访问指针。
有循环单链表和循环双链表：
循环单链表：
代码：区别在于闭环代码：
结构区别核心闭环在最后结点C时，next重新指向A，不再是null，后一个结点无限循环
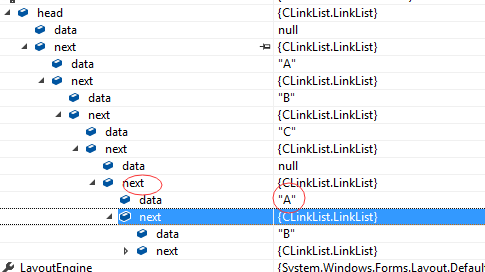
循环双链表：
代码：区别在于闭环代码：
结构区别核心：后一个结点和前一个结点都是无限循环
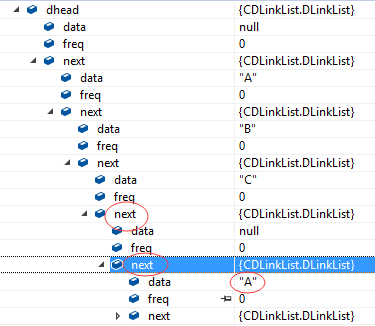
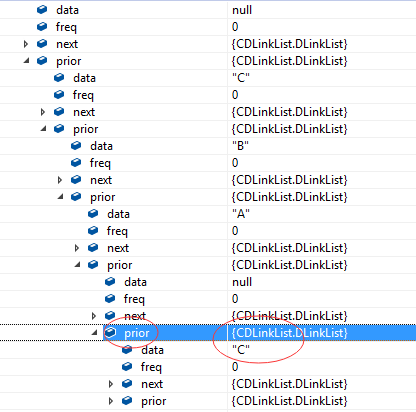
栈和队列：
栈
栈是什么：
是计算机科学中的一种抽象数据类型，只允许在有序的线性数据集合的一端（称为堆栈顶端，英语：top）进行加入数据（英语：push）和移除数据（英语：pop）的运算。因而按照后进先出（LIFO, Last In First Out）的原理运作。
顺序栈：是采用顺序存储结构，是分配一块连续的内存空间来存放栈中元素，并用一个变量top指向当前的栈顶以反映栈中元素的变化。
链栈：采用链式存储的栈成为链栈，优点是不需要考虑栈满溢出的情况。
实践项目： 简单算术表达式求值（ExpValue）、用栈求解迷宫问题（Maze2）
队列是什么：
队列又称为伫列（queue），是先进先出（FIFO, First-In-First-Out）的线性表。在具体应用中通常用链表或者数组来实现。队列只允许在后端（称为rear）进行插入操作，在前端（称为front）进行删除操作。
队列的操作方式和堆栈类似，唯一的区别在于队列只允许新数据在后端进行添加。
顺序队列：是采用顺序存储结构
循环队列：为了能够充分利使用数组data中的存储空间，把数组的前端和后端链接起来形成一个循环的顺序表，称为循环队列，四要素如下：（队头front、队尾指针rear、数组最大长度MaxSize，string[]数组data[]），奇怪的公式？
- 队空的条件：front==rear
- 队满的条件：(rear+1)%MaxSize==front
- 元素e进队操作：rear=(rear+)%MaxSize; e=data[ rear ]
- 元素e出队操作：front=(front+1)%MaxSize; e=data[ front ]
实践项目：SqQueue
链队：队列的链式存储结构也是通过结点构成的单链表实现的，此时只允许在单链表的表首进行删除操作和在单链表表尾进行插入操作，因此需要使用两个指针（队首指针front、队尾指针rear），类似双链表
实践项目：LinkQueue
队列实践项目：用队列求解迷宫（Maze3），与栈迷宫相似
串：
串是什么：是由零个或多个字符组成的优先序列。例如：str="a1a2a3...An"
子串：一个串中任意连续的字符组成的自诩列称为该串的子串。例如：a、ab、abc、abcd都是abcde的子串，空串是任意串的子串
主串：包含子串的称为主串。
串的模式匹配：
串的模式匹配也称为子串的定位操作，即查找子串在主串中出现的位置。设有主串S和子串T，如果在主串S中找到一个与子串T相相等的串，则返回串T的第一个字符在串S中的位置。其中，主串S又称为目标串，子串T又称为模式串。本文主要介绍两种常用的模式匹配算法，即朴素模式匹配算法——BF算法和改进算法——KMP算法。
实践项目：StringMatch
数组和广义表：
是由相同类型的元素（element）的集合所组成的数据结构，分配一块连续的内存来存储。利用元素的索引（index）可以计算出该元素对应的存储地址。
一维（或单维）数组：
是一种线性数组，其中元素的访问是以行或列索引的单一下标表示，例如：int[] array = new int[5];
多维数组：
普通数组采用一个整数来作下标。多维数组（高维数组）的概念特别是在数值计算和图形应用方面非常有用。我们在多维数组之中采用一系列有序的整数来标注，如在[ 3,1,5 ] 。这种整数列表之中整数的个数始终相同，且被称为数组的“维度”。关于每个数组维度的边界称为“维”。维度为k的数组通常被称为k维。例如：int[,] array = new int[4, 2];
交叉数组：
交错数组是元素为数组的数组。 交错数组元素的维度和大小可以不同。 交错数组有时称为“数组的数组”。例如：int[][] jaggedArray = new int[3][];
稀疏矩阵：
矩阵中非零元素的个数远远小于矩阵元素的总数，并且非零元素的分布没有规律，通常认为矩阵中非零元素的总数比上矩阵所有元素总数的值小于等于0.05时，则称该矩阵为稀疏矩阵(sparse matrix)，该比值称为这个矩阵的稠密度；与之相区别的是，如果非零元素的分布存在规律（如上三角矩阵、下三角矩阵、对角矩阵），则称该矩阵为特殊矩阵。
实践项目：SMatrix
广义表：
是一种非线性的数据结构，是线性表的推广（可以是线性结构，也可以不是线性结构）。但如果广义表的每个元素都是原子，它就变成了线性表。广义表广泛地用于人工智能等领域的LISP语言。
存储结构：广义表是一种递归的数据结构，因此很难为每个广义表分配固定大小的存储空间，所以其存储结构只有采用动态链式结构。
类似双链表？
实践项目：GeneralTable
树和二叉树：
C#中的树：
个人理解：树就是有父节点和子节点组成，一个父节点由一个或者多个子节点，一个子节点再由一个或者多个子节点组成，形成的就是树
树是什么：树是一种非线性结构，它特别适合于表示层次结构的数据。树的定义是递归的。
在计算机科学中，树（英语：tree）是一种抽象数据类型（ADT）或是实现这种抽象数据类型的数据结构，用来模拟具有树状结构性质的数据集合。它是由n（n>0）个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：
- 每个节点都只有有限个子节点或无子节点；
- 没有父节点的节点称为根节点；
- 每一个非根节点有且只有一个父节点；
- 除了根节点外，每个子节点可以分为多个不相交的子树；
- 树里面没有环路(cycle)
树的种类：
- 无序树：树中任意节点的子节点之间没有顺序关系，这种树称为无序树，也称为自由树；
- 有序树：树中任意节点的子节点之间有顺序关系，这种树称为有序树；
树的表示方法：
- 图像表达法（点击图片查看动态图）
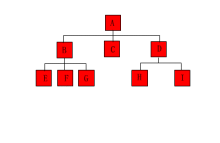符号表达法：A ( B ( D ( , G ) ) , C ( E , F ) )
- 一级：A的左节点是B，右节点是C
- 二级：B的左节点是D，右边没有； C的左节点是E，右节点是F
- 三级：D的左节点没有，右节点是G
- 一共有4个父节点：A、B、D、C
- 遍历表达法
- 先序遍历（当前节点、左节点、右节点顺序）：A B D G C E F
- 中序遍历（左节点、当前节点、右节点顺序）：D G B A E C F
- 后序遍历（左节点、右节点、当前节点顺序）：G D B E F C A
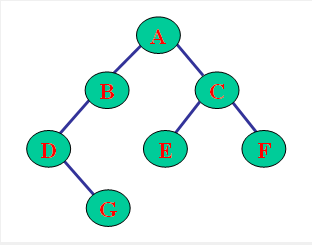
二叉树：每个节点最多含有两个子树的树称为二叉树
二叉树中序遍历（左节点、当前节点、右节点顺序）执行顺序说明：
递归内开始有三行代码（每个子递归也会有这三行代码）：递归左节点B ==》拼接当前节点A ==》递归右节点C，每个递归节点都会有这三行代码，一直递归到最后结点，从最后结点开始拼接，具体按照下面顺序：
1 递归左节点B
1.1 递归左节点D
1.1.1 递归左节点null
1.1.2 拼接当前节点D
1.1.3 递归右节点G
1.1.3.1 递归左节点null
1.1.3.2 拼接当前节点G
1.1.3.3 递归右节点null
1.2 拼接当前节点B
1.3 递归右节点null
2 拼接当前节点A
3 递归右节点C
3.1 递归左节点E
3.1.1 递归左节点null
3.1.2 拼接当前节点E
3.1.3 递归右节点null
3.2 拼接当前节点C
3.3 递归右节点F
3.3.1 递归左节点null
3.3.2 拼接当前节点F
3.3.3 递归右节点null
private void InOrder1(BTNode t) //二叉树中序遍历法，输出结果：D G B A E C F { if (t != null) { InOrder1(t.lchild); //1 递归左节点 btstr += t.data.ToString() + " "; //2 拼接当前节点 InOrder1(t.rchild); //3 递归右节点 } }
调式跟踪的结构：
lchild是左节点，rchild是右节点
父节点：A、C、D， （怎么没有B？）
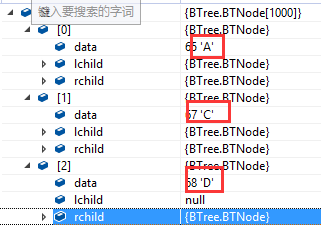
详细看A节点，已经包含了整个二叉树：顶头是A，左边是B D G，右边是C E F
构造二叉树：
例如：先序序列ABDGCEF + 中序序列DGBAECF 构造成A(B(D(,G)),C(E,F))
实践项目是CreateBTree
线索二叉树：
定义：
在二叉树的结点上加上线索的二叉树称为线索二叉树，对二叉树以某种遍历方式（如先序、中序、后序或层次等）进行遍历，使其变为线索二叉树的过程称为对二叉树进行线索化。
本质：
二叉树的遍历本质上是将一个复杂的非线性结构转换为线性结构，使每个结点都有了唯一前驱和后继（第一个结点无前驱，最后一个结点无后继）。对于二叉树的一个结点，查找其左右子女是方便的，其前驱后继只有在遍历中得到。为了容易找到前驱和后继，有两种方法。一是在结点结构中增加向前和向后的指针，这种方法增加了存储开销，不可取；二是利用二叉树的空链指针。
实践项目：第6章 Thread
红黑树：
c#中的红黑树：TreeSet类，SortedDictionary
图：
哈希表：
加密时，字符越长越不容易破解
C#的哈希表类：System.Collections.Hashtable
哈希查找时不用遍历，直接根据key找values