队列的介绍和简单使用（二）

队列，和栈一样，也是一种对数据的"存"和"取"有严格要求的线性存储结构。

与栈结构不同的是，队列的两端都"开口"，要求数据只能从一端进，从另一端出

通常，称进数据的一端为 "队尾"，出数据的一端为 "队头"，数据元素进队列的过程称为 "入队"，出队列的过程称为 "出队"。

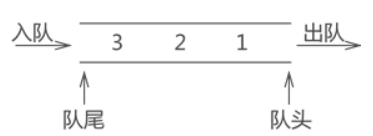
 不仅如此，队列中数据的进出要遵循 "先进先出" 的原则，即最先进队列的数据元素，同样要最先出队列。拿图 1 中的队列来说，从数据在队列中的存储状态可以分析出，元素 1 最先进队，其次是元素 2，最后是元素 3。此时如果将元素 3 出队，根据队列 "先进先出" 的特点，元素 1 要先出队列，元素 2 再出队列，最后才轮到元素 3 出队列。

栈和队列不要混淆，栈结构是一端封口，特点是"先进后出"；而队列的两端全是开口，特点是"先进先出"。

因此，数据从表的一端进，从另一端出，且遵循 "先进先出" 原则的线性存储结构就是队列。

队列的实现

队列存储结构的实现有以下两种方式：

1. 顺序队列：在顺序表的基础上实现的队列结构；
2. 链队列：在链表的基础上实现的队列结构；

两者的区别仅是顺序表和链表的区别，即在实际的物理空间中，数据集中存储的队列是顺序队列，分散存储的队列是链队列。

顺序队列简单实现

由于顺序队列的底层使用的是数组，因此需预先申请一块足够大的内存空间初始化顺序队列。除此之外，为了满足顺序队列中数据从队尾进，队头出且先进先出的要求，我们还需要定义两个指针（top 和 rear）分别用于指向顺序队列中的队头元素和队尾元素

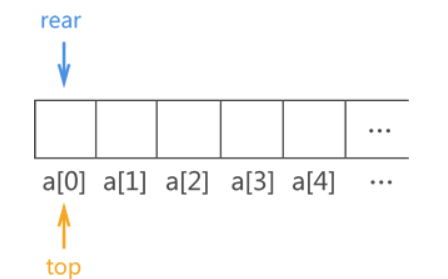
由于顺序队列初始状态没有存储任何元素，因此 top 指针和 rear 指针重合，且由于顺序队列底层实现靠的是数组，因此 top 和 rear 实际上是两个变量，它的值分别是队头元素和队尾元素所在数组位置的下标。

当有数据元素进队列时，对应的实现操作是将其存储在指针 rear 指向的数组位置，然后 rear+1；当需要队头元素出队时，仅需做 top+1 操作。

{1,2,3,4} 用顺序队列存储的实现操作

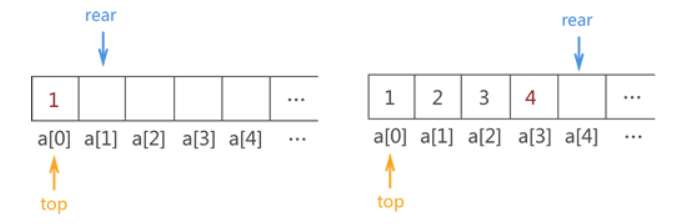
顺序队列中数据出队列的实现过程

 

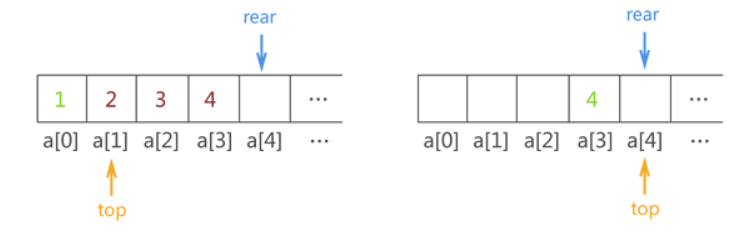
此方法存在的问题

我们希望的是当 rear和top相等的时候就说队列为空。可是通过数据全部出队后的示意图。会发现，指针 top 和 rear 重合位置指向了  a[4] 而不再是 a[0]。也就是说，整个顺序队列在数据不断地进队出队过程中，在顺序表中的位置不断后移。

顺序队列整体后移造成的影响是：

• 顺序队列之前的数组存储空间将无法再被使用，造成了空间浪费；
• 如果顺序表申请的空间不足够大，则直接造成程序中数组 a 溢出，产生溢出错误；

循环队列简单实现

既然明白了上面这种方法的弊端，那么我们可以试着在它的基础上对其改良。

为了解决以上两个问题，可以使用巧妙的方法将顺序表打造成一个环状表

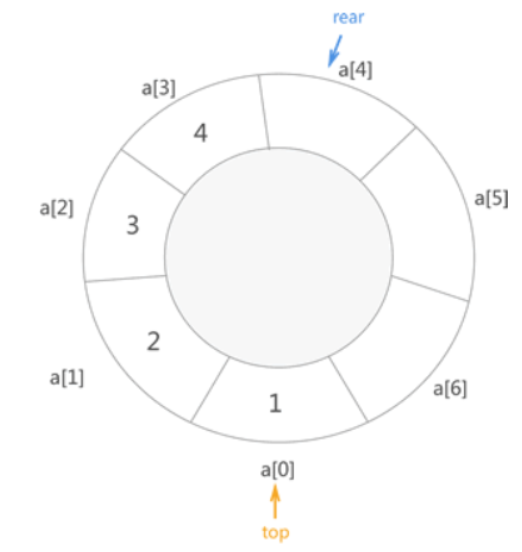
top和rear相等时说明队列为空。（rear+1）% 数组长度 == top时说明队满 
比如上面这个当rear在a[5]时说明队满。会有一个空间浪费

java实现循环队列

package com.qiaorui;

public class LoopQueue<E> {
    private E data[];
    private int top, rear;

    public LoopQueue(int capacity) {
        this.data = (E[]) new Object[capacity + 1];
        this.top = 0; // 头指针
        this.rear = 0; // 尾指针
    }

    public LoopQueue() {
        this(10);
    }

    public int getCapacity() {
        return data.length - 1;
    }

    public boolean isEmpty() {
        return top == rear;
    }

    public void enqueue(E e) {
        if ((rear + 1) % data.length == top) {
            resize(getCapacity() * 2); //扩容
        }
        data[rear] = e;
        rear = (rear + 1) % data.length;
    }

    public E dequeue() {
        if (isEmpty())
            throw new IllegalArgumentException("Cannot dequeue from an empty queue.");
        E ret = data[top];
        data[top] = null;
        top = (top + 1) % data.length;
        if ((rear - top + data.length) % data.length == getCapacity() / 4 && getCapacity() / 2 != 0)
            resize(getCapacity() / 2);
        return ret;
    }

    public E getFront() {
        if (isEmpty())
            throw new IllegalArgumentException("Queue is empty.");
        return data[top];
    }

    private void resize(int newCapacity) {
        E[] newData = (E[]) new Object[newCapacity + 1];
        //如果rear<top结果是rear-top+maxsize
        //如果rear>top结果是rear-top
        //为了用一个表达式同时表达两者，用(rear-top+maxsize)%maxsize
        for (int i = 0; i < (rear - top + data.length) % data.length; i++)
            newData[i] = data[(i + top) % data.length]; //从头指针开始把元素放入新的数组中
        this.rear = (rear - top + data.length) % data.length; //这个一定要在缩容前赋值
        this.data = newData; //缩容
        this.top = 0;

    }

    public String toString() {

        StringBuilder res = new StringBuilder();
        res.append(String.format("Queue: size = %d , capacity = %d
", (rear - top + data.length) % data.length, getCapacity()));
        res.append("front [");
        //遍历方式 2
        for (int i = top; i != rear; i = (i + 1) % data.length) {
            res.append(data[i]);
            if ((i + 1) % data.length != rear) {
                res.append(", ");
            }
        }
        res.append("] tail");
        return res.toString();
    }

    public static void main(String[] args) {

        LoopQueue<Integer> queue = new LoopQueue();
        for (int i = 0; i < 10; i++) {
            queue.enqueue(i);
            System.out.println(queue);

            if (i % 3 == 2) {
                queue.dequeue();
                System.out.println(queue);
            }
        }
    }

}

简单使用

力扣 933题
https://leetcode-cn.com/problems/number-of-recent-calls/

class RecentCounter {
 private Queue<Integer> queue =new LinkedList<Integer>();

    public RecentCounter() {
       
    }

    public int ping(int t) {
        queue.offer(t);
        while (queue.peek() < t - 3000)
            queue.poll();
        return queue.size();
    }
}