有一维数组 [x1,x2...xn],要求一个值X,使得:
F(X) = (X-x1)2+(X-x2)2+...(X-xn)2 = min
F(X) = nX2 - 2 * (x1+x2+....+xn) + x12 + x22 + ...+xn2 = min
对X求导,当dF/dX = 0时,F(X)有极小值;
2nX - 2 (x1+x2+....+xn) = 0
那么,X = (x1+x2+....+xn) / n
因此,在一维的情况下,最小二乘求参数X,和求均值一样;
使用矩阵的方法,先建立方程组:
X - x1 = 0
...
X - xn = 0
也就是方程组:
An*1X =b,等价于 [1,1,......] T X = [x1,x2...xn] T;
ATAX = ATb
同样解得:X = (x1+x2+....+xn) / n
应用:在一维中,有[2,2,2,2,2,10]这样子的数组,找出其中的孤值
先求出 X = 均值 = 3.333
中误差 = sqrt [ [(2-3.333)2 + (2-3.333)2 + (2-3.333)2 + (2-3.333)2 + (2-3.333)2 + (10-3.333)2 ] / (6-1) ] = 3.1622
假如一维数组是对一段距离的观测值,假设服从正态分布N[ μ,σ2] , u应该是接近2的数字,但实际上是不可知道的,样本量大时,通常用X和中误差来代替
|xn - u| > 2σ 的概率,为 1 - 95.449974%;
|xn - u| > 3σ 的概率,为 1 - 99.730020%;
所以,基于这个原理,|10 - 3.3333 | ≈ 2σ ,是属于小概率事件,所以认为10是孤值;
加权最小二乘法;
假如,为上面每个数字,求加权平均值,假如权值分别为[p1,p2....pn],假如为[1,1,1,1,1,1/5]
加权并不是:X =( 2+ 2 + 2 + 2 +2 + 1 / 5 * 10 )/ 6 = 2;
而是F(X) = p1(X-x1)2+p2(X-x2)2+...p3(X-xn)2 = min
F'(X) = 2 (p1 + p2 + ... pn) - 2 (p1x1 + p2x2 + ... + pnXn)
因此X = (p1x1 + p2x2 + ... + pnXn) / (p1 + p2 +...+pn) = 12 / 5.2 = 2.3
如同解 ATPAX = ATPb
p越大,说明对某个观测值越信赖,对其误差也越信赖;
关于误差传播
假如x经过n次读数,其中误差 = Σ(xi - xavg)² / n,用矩阵的形式,就是Dxx = [x1-xavg ,x2-xavg,... xn-xavg] [x1-xavg ,x2-xavg,... xn-xavg] T / n
* 定义函数E(x)为求x的均值,那么Dxx = E[ [x1-xavg ,x2-xavg,... xn-xavg] [x1-xavg ,x2-xavg,... xn-xavg] T]
假如 y = ax,那么,其中误差 = Σ(axi - axavg)² / n = a2 , 就是Dyy = a2 Dxx
因此,在一元的情况下 y = ax,y的方差D(Y) = a2 Dxx
多元的情况下:
z = ax - by ,用矩阵的形式表示,那么 Z = [a,b][x,y]T = KX
E(Z) = KE(X)
证明:
E(X) = [E(x),E(y)]T
E(Z) = ∑z / n = a * ∑x / n + b∑y / n = aE(x) + bE(y) = K[E(x),E(y)]T = KE(X)
D(Z) = E ( [Z-E(Z)] [Z-E(Z)]T)
= E ( [KX - KE(X)] [ KX - KE(X)]T)
= E ( K[X - E(X)] [ X - E(X)]T KT) (KA)T = ATKT
= KE ( [X - E(X)] [ X - E(X)]T ) KT
Dxx = E ( [X - E(X)] [ X - E(X)]T ) = [x-xavg ,y-yavg ] T [x-xavg ,y-yavg ] / n
X = [x,y]T , E(X) = [E(x),E(y)]T
因此,Dxx 对角 (x-E(x))(x-E(x))T / n,为x的方差; (y-E(y))(y-E(y))T / n 为y的方差;
非对角 (x-E(x))(y-E(y))T / n ,为x和y的协方差;
协方差的本质,是形容X的曲线,和Y的曲线的相似程度,其横轴均为样本序列
在实际解算的时候,如果两种观测量(x和y)是完全不相关的,例如: x代表测角、y代表测距 ,即使(x-E(x))(y-E(y))T / n ≠ 0,在Dxx的非对角处,任然写为0值;
因此求Dzz要追根朔源
假如有:
z1 = a1x + b1y
z2 = a2x + b2y
z1和z2如何才是独立观测量,完全不相关?
等价于Dzz,非对角线元素为0
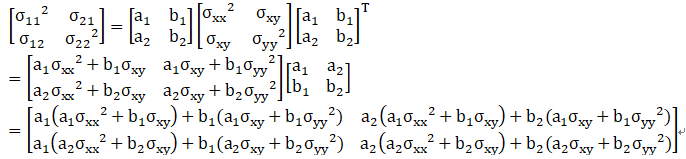
隐含条件:
1. a1、b1不能同时为0 ,否则相当于Z1没有意义;
2. a2、b2不能同时为0 ,否则相当于Z2没有意义;
3. σxx 和 σyy 均不能等于0,否则解算没有意义,因为没有误差传递;
那么,要使得非对角线为0,那么:
1. a1 = 0 ,b2 = 0, σxy = 0;
1. b1 = 0 ,a2 = 0, σxy = 0;
没有别的选择;
因此,x、y必须是独立观测的,不相关的观测量,而且,Z的方程组,每条方程的自变量均不相同,要么:
z1 = a1x
z2 = b2y
或者
z1 = b1y
z2 = a2x