Description
给定一棵 (n) 个点的树,还有 (m) 条非树边,问有多少种方法使得仅砍去一条树边和一条非树边使得这个图分成不相连的两(或更多)部分。
每次如果先砍去主要边后已经砍成两半,则仍要再砍一条附加边。
Solution
一看这数据范围,暴力组合肯定不可行。
思考附加边的作用:在这棵仅有主要边的数上,增加了一条附加边就会多一个带有根节点的环。
具体看一个例子:
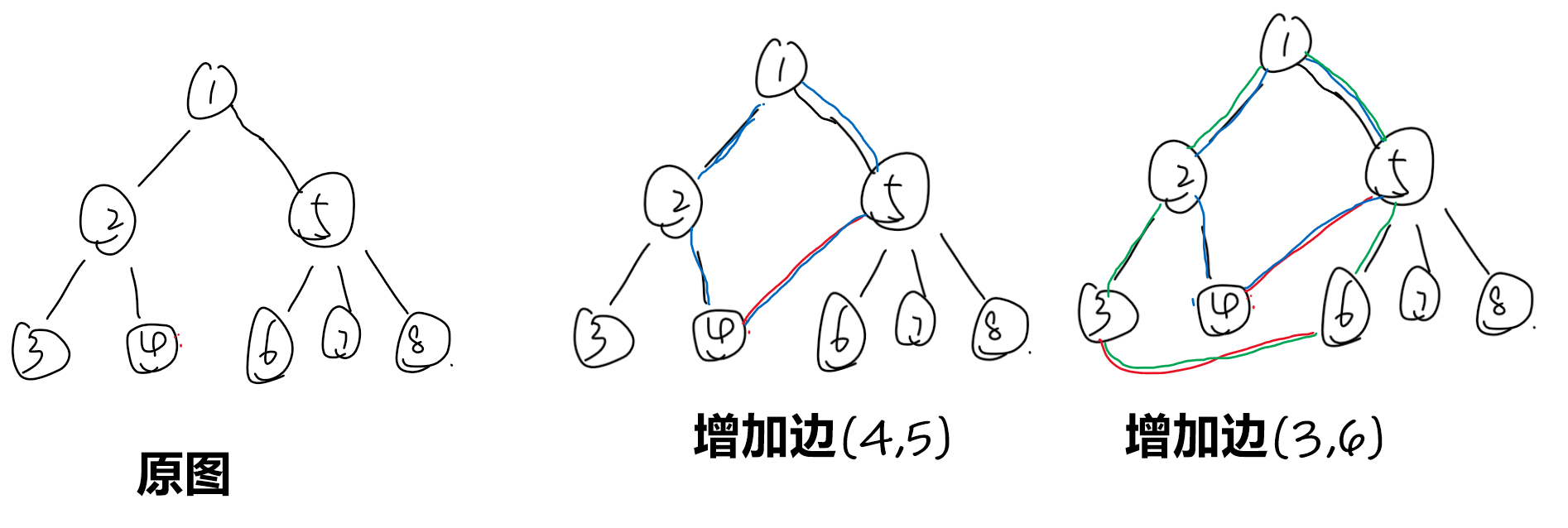
如图,在增加边 ((4,5)) 后,出现了 (1-2-4-5) 的蓝颜色环,如果在加一条边 ((3,6)),则还会出现 (1-2-3-5-6) 这一个绿颜色环。
在一个环上,要砍成两部分,就需要把这个环给打断。先切断一条主要边,再把形成这个环的那个附加边去除。因此把环一分为二需要断2条边才能断开。
设 (sum[i]) 表示以 (1) 为根,(i) 号点与它的父亲节点连接的主要边砍掉后,还要砍掉多少条附加边才能把这个图一分为二。
即每新增一条附加边,由于环上的点需要把这条附加边砍去才能断开这个环,所以这个环的每一条主要边的 (sum) 值均需要 (+1)。
具体长这个样子:
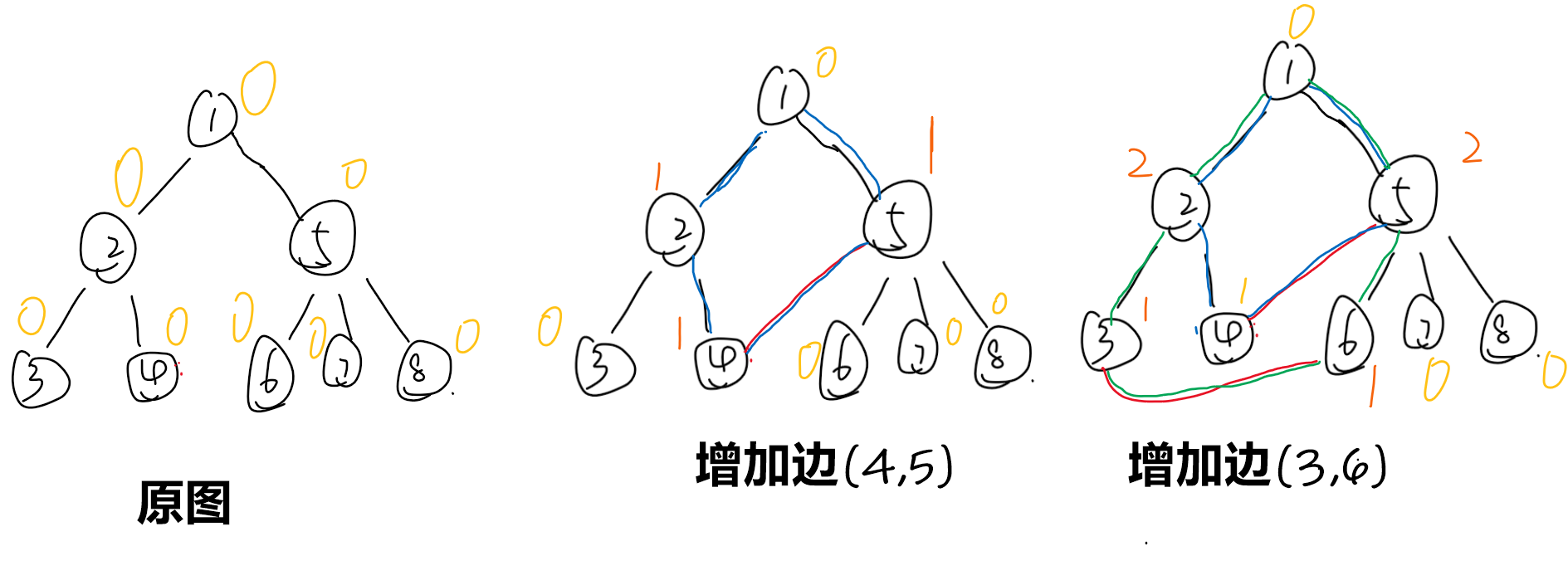
最后要把sum的值分三类:
-
(sum[i] = 0),表示这个点没被任意一个环覆盖过,说明删掉这条边就已经变成两部分了,这个点有 $m $ 种方案。
-
(sum[i] = 1),表示这个点被一个环覆盖过,只能删除这个边后再删那个组成环的附加边,这个点有$ 1$ 种方案。
-
(sum[i] ≥ 2),表示这个点被多个环覆盖过,则不管怎样删也不能把图一分为二,这个点没有方案贡献。
现在就是考虑如何维护这个 (sum) 数组。
不难想到用树上差分+前缀和来写。
这里的前缀和采取的是第二种,即从以这个点为根的子树的和。
根据树上差分知识,可以把该条附加边连接的两点 (x),(y) 的 (sum) 均 (+1),把 (LCA(x, y)) 的值 (-2)。
然后用DFS跑一边数上前缀和就行了。
Code
// by pjx Jul.
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <queue>
#include <stack>
#define REP(i, x, y) for(register int i = x; i < y; i++)
#define rep(i, x, y) for(register int i = x; i <= y; i++)
#define PER(i, x, y) for(register int i = x; i > y; i--)
#define per(i, x, y) for(register int i = x; i >= y; i--)
#define lc (k << 1)
#define rc (k << 1 | 1)
using namespace std;
#define int long long
const int N = 1E5 + 5;
const int M = 2 * N;
struct node{
int u, v, next;
}ed[M];
int head[M], dep[N], f[N][21], sum[N];
int n, m, cnt;
bool b[N];
void add(int u, int v)
{
cnt++;
ed[cnt].u = u;
ed[cnt].v = v;
ed[cnt].next = head[u];
head[u] = cnt;
}
void dfs(int x)//第一遍DFS预处理出LCA要用的f数组
{
for(int i = 1; i <= 20; i++)
{
f[x][i] = f[f[x][i - 1]][i - 1];
}
for(int i = head[x]; i != 0; i = ed[i].next)
{
int v = ed[i].v;
if(!b[v])
{
b[v] = 1;
dep[v] = dep[x] + 1;
f[v][0] = x;
dfs(v);
}
}
}
void dfs2(int x)//第二遍DFS就是求前缀和
{
for(int i = head[x]; i != 0; i = ed[i].next)
{
int v = ed[i].v;
if(!b[v])
{
b[v] = 1;
dfs2(v);
sum[x] += sum[v];
}
}
}
int lca(int x, int y)
{
if(dep[x] < dep[y])
{
swap(x, y);
}
int temp = dep[x] - dep[y];
for(int i = 19; i >= 0; i--)
{
if(temp & (1 << i))
{
x = f[x][i];
}
}
if(x == y)
{
return x;
}
for(int i = 19; i >= 0; i--)
{
if(f[x][i] != f[y][i])
{
x = f[x][i];
y = f[y][i];
}
}
return f[x][0];
}
signed main()
{
cin >> n >> m;
rep(i, 1, n - 1)
{
int x, y;
cin >> x >> y;
add(x, y);
add(y, x);
}
b[1] = 1;
dep[1] = 1;
dfs(1);
rep(i, 1, m)
{
int x, y;
cin >> x >> y;
sum[x]++;//树上差分
sum[y]++;
//cout << lca(x, y) << endl;
sum[lca(x, y)] -= 2;
}
memset(b, 0, sizeof b);
b[1] = 1;
dfs2(1);
int ans = 0;
for(int i = 2; i <= n; i++)
{
if(sum[i] == 0)//分类讨论三种sum值情况
{
ans += m;
}
else if(sum[i] == 1)
{
ans++;
}
}
cout << ans;
return 0;
}