算法思想:分而治之
1)选择一个基准数,通常选择第一个数或者最后一个数;
2)通过一趟排序将待排序的记录分割成独立的两部分,即从数组两头向中心搜索,如果左边发现大于基准值且右边发现小于基准值的数,则这两个数据交换位置;
3)左右两侧搜索指针相遇,当前值与基准值比较,如果小于基准值则互换位置,此时基准元素在其排好序后的正确位置,它左边的数都比它小,右边的都比它大;
4)然后分别对这两部分记录用同样的方法继续进行排序,直到整个序列有序。
在平均状况下,快速排序 n 个数据要Ο(n log n)次比较。在最坏状况下则需要Ο(n2)次比较,但这种状况并不常见。事实上,快速排序通常明显比其他Ο(n log n) 算法更快,因为它的内部循环(inner loop)可以在大部分的架构上很有效率地被实现出来,且在大部分真实世界的数据,可以决定设计的选择,减少所需时间的二次方项的可能性。
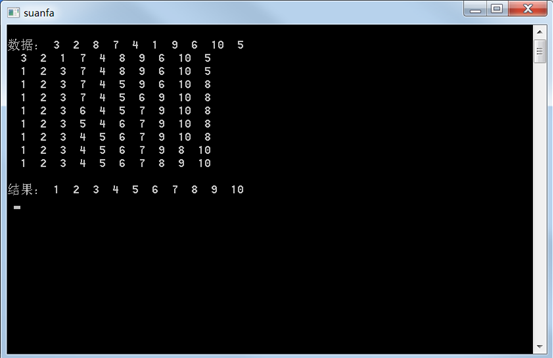
1 int main(int argc, _TCHAR* argv[]) 2 { 3 int a[10] = {3,2,8,7,4,1,9,6,10,5}; 4 5 printf(" 数据:"); 6 print(a,10); 7 quicksort(a,0,9); 8 printf(" 结果:"); 9 print(a,10); 10 getchar(); 11 return 0; 12 } 13 14 void print(int a[], int n){ 15 for(int j= 0; j<n; j++){ 16 printf(" %d ", a[j]); 17 } 18 printf(" "); 19 } 20 21 void quicksort(int v[], int left, int right) 22 { 23 if(left < right) 24 { 25 int tmp =0; 26 int key = v[left]; 27 int low = left; 28 int high = right; 29 while(low < high){ 30 while(low < high && v[high] > key){ 31 high--; 32 } 33 while(low < high && v[low] <= key){ 34 low++; 35 } 36 if(low!=high){ 37 tmp = v[low]; 38 v[low] = v[high]; 39 v[high] = tmp; 40 print(v,10); 41 } 43 } 44 45 if(key > v[low]) 46 { 47 v[left]= v[low]; 48 v[low]=key; 49 print(v,10); 50 } 51 52 quicksort(v,left,low-1); 53 quicksort(v,low+1,right); 54 } 55 }
运行结果: