一. 普通全连接神经网络的计算过程
假设用全连接神经网络做MNIST手写数字分类,节点数如下:
第一层是输入层,784个节点;
第二层是隐层,100个节点;
第三层是输出层,10个节点。
对于这个神经网络,我们在脑海里浮现的可能是类似这样的画面:

但实际上,神经网络的计算过程,本质上是输入向量(矩阵)在权重矩阵上的流动过程,大概就像下面这个过程:

图中,把bias也放到权重矩阵中了,并且省略了激活函数。在反向传播过程中,梯度矩阵和权重矩阵的大小是一致的,因为每个权重参数都需要一个梯度来更新。神经网络的学习过程,实际上是调整权重矩阵中各个元素的大小的过程。
二. LSTM神经网络的参数数目
lstm的计算公式是

假设input_size=150,hidden_size=64,那么
- $W_{ii}$、$W_{if}$、$W_{ig}$、$W_{io}$的大小都是64*150的矩阵,$b_{ii}$、$b_{if}$、$b_{ig}$、$b_{io}$都是长度为64的向量;
- $W_{hi}$、$W_{hf}$、$W_{hg}$、$W_{ho}$的大小都是64*64的矩阵,$b_{hi}$、$b_{hf}$、$b_{hg}$、$b_{ho}$都是长度为64的向量。
在PyTorch的torch.nn.LSTM模块中,会把几个向量按0方向拼接在一起:
- 把$W_{ii}$、$W_{if}$、$W_{ig}$、$W_{io}$拼接成一个大小为256*150矩阵,叫做weight_ih_l0;把$b_{ii}$、$b_{if}$、$b_{ig}$、$b_{io}$拼接成一个长度为256的向量,叫做bias_ih_l0;
- 把$W_{hi}$、$W_{hf}$、$W_{hg}$、$W_{ho}$拼接成一个大小为256*64矩阵,叫做weight_hh_l0;把$b_{hi}$、$b_{hf}$、$b_{hg}$、$b_{ho}$拼接成一个长度为256的向量,叫做bias_hh_l0.
所以总的参数数目是256*150 + 256 + 256*64 + 256 = 55296.
归纳一下就是:
假设input_size=x,hidden_size=h,那么这个LSTM模型的参数数目就是:4*h*x + 4*h + 4*h*h + 4*h = 4*h*(x+h+2)
三. LSTM神经网络的计算过程
假设input_size=150,hidden_size=64,那么单个时间步的计算过程如下:
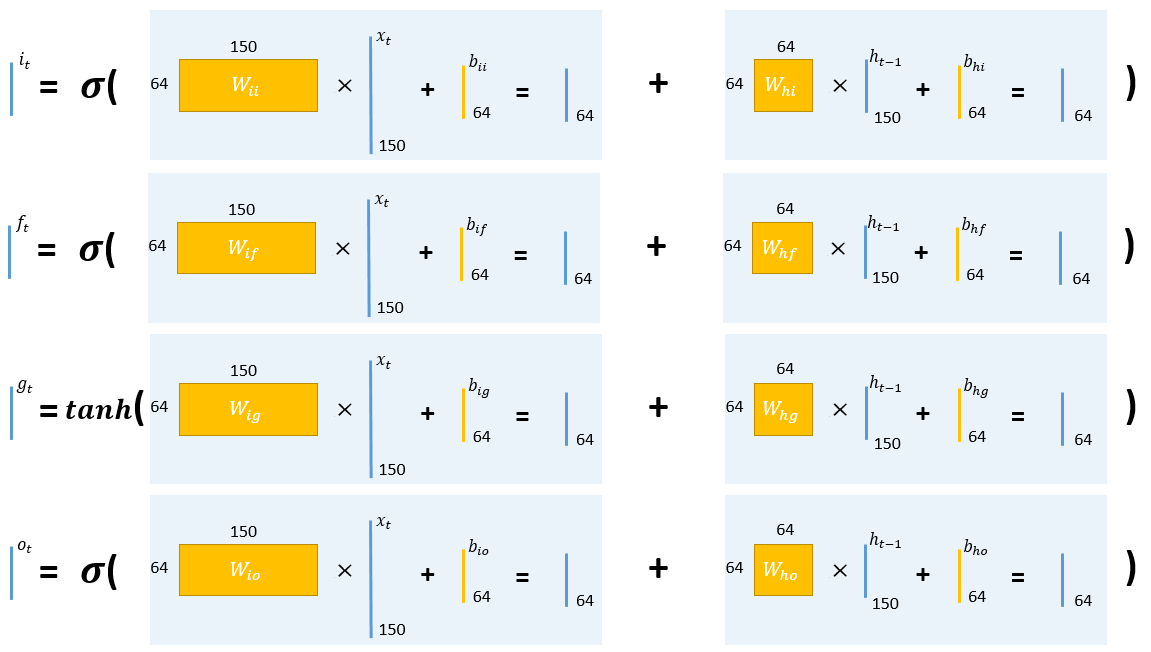

星号*表示逐元素相乘。
【参考资料】