1 树
树是一种数据结构,既能像链表那样快速的插入和删除,又能像有序数组那样快速查找,树是非常好的数据结构。本章重点介绍的是一种特殊的树————二叉树。
树是由边链结的结点组成,结点通常代表的是其他常用数据结构中存储的数据项。边的意思是从一个结点到另一个结点,在Java中就用引用来表示。计算机里面的树数据结构的拓扑图和真实的树相比是倒过来的。树的每一层结点都可以和下一层多个结点相连接,这里讨论的是二叉树,每一个结点最多有两个子节点。在更普通的树里面,结点的子结点可以多于两个,这种树叫多路树。后面的2-3-4 树可以看到多路数的例子。

路径
路径是顺着连接结点的边从一个结点走到另一个结点,所经过的结点的顺序排列就称为路径。
根
树顶端的结点称为根,一棵树只有一个根,如果要把一个结点和边的集合定义为树,那么从根到其他任何一个结点的路径都必须有而且只有一条,超过一条路径或没有路径到达,都不是树。
父结点(节点)
每个结点除了根都恰好有一条边向上连接到另一个结点,上面的这个结点就称为下面的结点的父结点。
子节点
除了根节点外的其他所有结点都可以被称为子节点。
叶结点
没有子结点的结点称为叶子结点或简称叶结点。
子树
每个结点都可以作为子树的根,它和它所有的子结点,子结点的子结点都包含在子树中。
访问
当程序控制流程到达某个结点时,就称为访问这个结点,通常为了这个结点进行某种操作。
遍历
遍历树意味着遵循某种特定的顺序访问树中的所有结点。
层
一个结点所在的层数,是从根开始,将根到该结点的路径拉直,结点的索引号,就是层数。
二叉树
如果树中每个结点最多只能有两个子结点,这样的树就成为二叉树,二叉树每个结点的两个子结点称为左子结点和右子结点。
二叉树在学术上称为二叉搜索树。二叉搜索树特征的定义可以这样说:一个结点的左子结点的关键字值小于这个结点,右子结点的关键字值大于或等于这个父结点。

非平衡树
一个树的平衡性是根据下面的标准判定的:如果树的某个结点只有一个子结点,而另一边没有子结点,并且大部分结点都在一边或另一边,这个树就是非平衡的。
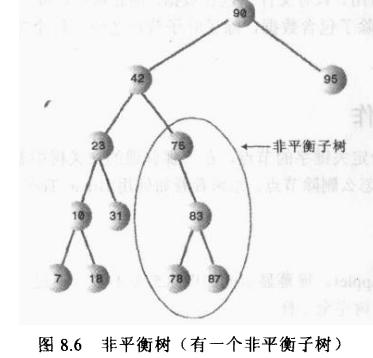
树变得不平衡的原因是由于插入数据项时候按照一定顺序插入导致的,如果是随机插入,树多少会更平衡一点,如果插入的顺序是升序比如,1,2,3,4,5 等等或是降序,则所有的值都是右子结点(升序),或者都是左子结点(降序),这样树就会不平衡了。树的不平衡性会导致效率严重退化。如果全在右子结点,很显然,程序需要循环到第四层才能找到5,但是如果是平衡的,那么最差也会在第三层找到,对于大数据量的情况下,这种反差更加明显。
下面来实现一个二叉树
对于结点的连接,显然我们依然需要使用引用来表示。
Node类
首先需要有一个结点对象的类,这些对象包含数据,数据代表存储内容,而且还有指向结点的两个子结点的引用。
class Node{ int iData; double fData; Node leftChild; Node rightChild; public void displayNode(){ } }
Tree类
还需要有一个类表示树的本身。
class Tree{ private Node root; public void find(int key){ } public void insert(int id, double dData){ } public void delete(int id){ } }
我们逐个来实现上面对于树的find、insert和delete算法。
1.1 查找算法
我们知道二叉树的左子结点是放小于父结点的值的,右子结点是存放大于父结点的值的。

public Node find(int key){ Node current = root; while(current.iData != key){ if(key < current.iData){ current = current.leftChild; }else{ current = current.rightChild; } if(current == null){ return null; } } return current; }
树的时间复杂度是O(logN)
1.2 插入一个结点
要插入一个结点,必须先找到插入的地方。先找到父结点,然后就可以插入的左子结点或右子结点。

public void insert(int id, double dd){ //新插入的结点 Node newNode = new Node(); newNode.iData = id; newNode.dData = dd; //如果树是空的 if(root == null){ root = newNode; //树不空 }else{ Node current = root; Node parent; while(true){ parrent = current; //左子结点值小于父结点 if(id < current.iData){ current = current.leftChild; if(current == null){ parent.leftChild = newNode; return; } //右子结点值大于父结点 }else{ current = current.rightChild; if(current == null){ parent.rightChild = newNode; return; } } } } }
1.3 遍历树
遍历树的意思是根据一种特定顺序访问数的每一个结点。这个过程不如查找、插入和删除结点常用,其中一个原因是遍历的速度不是特别快。有三种方法遍历树,它们是:前序、中序、后序,二叉搜索树最常用的遍历方法是中序遍历。先介绍中序遍历。
中序遍历
中序遍历二叉搜索树会使所有的结点按关键字值升序被访问到。遍历树的最简单方法是递归方法,用递归的方法遍历整棵树要用一个结点作为参数。初始化时这个结点是根,这个方法只需要做三件事:
1. 调用自身遍历结点的左子树
2. 访问这个结点
3. 调用自身来遍历结点的右子树
访问结点的意思是通常会对该结点进行一些操作,比如显示结点、把结点写入文件或其他别的操作。
遍历可以应用于任何二叉树。
private void inOrder(Node localRoot){ if(localRoot != null){ inOrder(localRoot.leftChild); System.out.print(localRoot.iData + " "); inOrder(local.rightChild); } }
遍历一棵三结点树
下面的示意图是遍历一棵三结点的树

前序和后序遍历
除了中序之外,还有两种遍历方法:它们是前序和后序。要中序遍历一棵树的原因是很清楚的,但要通过前序或后序来遍历树通常用于解析或分析代数表达式。这里暂时不介绍了。
1.4查找最大值和最小值
二叉搜索树得到最大值和最小值是很容易的事情。
要找到最小值,先走到根的左子结点处,然后接着走到那个子结点的左子结点,如此类推,直到找到没有一个左子结点的结点。这个结点就是最小值。
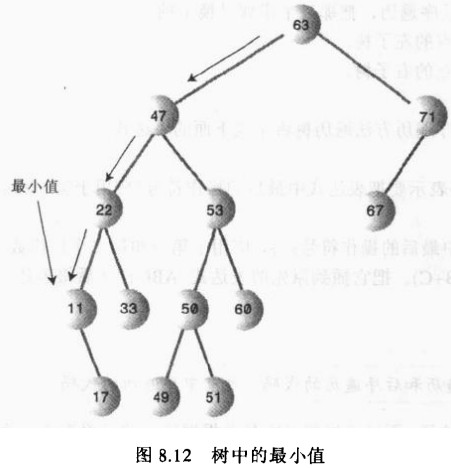
public Node minimum(){ Node current, last; current = root; while(current != null){ last = current; current = current.leftChild; } return last; }
类似地,要找到最大值,先从根结点开始,一直向右找到没有右子结点的结点,这个结点就是最大值的结点。
1.5 删除结点
删除结点是二叉搜索树常用的一般操作中最复杂的,但是又很重要。
删除结点要从查找要删除的结点开始入手,方法与前面介绍的find和insert相同,找到结点后,这个要删除的结点可能会有三种情况要考虑。
1. 该结点是叶子节点
2. 该结点有一个子结点
3. 该结点有两个子结点
情形1:删除没有子结点的结点
要删除叶结点,只需要改变该结点的父结点的对应子字段的值,由指向该结点改为null就可以了,要删除的结点仍然存在,但已经不是树的一部分了,java的垃圾自动收集机制会自动对它进行清除。
具体实现:
public boolean delete(int key){ Node current = root; Node parent = root; boolean isLeftChild = true; while(current.iData != key){ parent = current; if(key < current.iData){ isLeftChild = true; current = current.leftChild; }else{ isLeftChild = false; current = current.rightChild; } if(current == null){ return false; } } }
找到结点后,先要检查它是不是真的没有子结点,如果它没有子结点,还需要检查它是不是根。如果它是根的话,只需要把它置为null,这样就清空了整棵树。否则,就把父结点的leftChild或rightChild字段置为null,断开父结点和那个要删除结点的链接。
if(current.leftChild == null && current.rightChild == null){ if(current == root){ root = null; }else if(isLeftChild){ parent.leftChild = null; }else{ parent.rightChild = null; } }
情况2:删除有一个子结点的结点
这种情况也不是很难,这个结点只有两个结点:连向父结点和连向它唯一的子结点。只需要从这个序列中剪断这个结点,把它的子结点直接连到它的父结点上。这个过程要求改变父结点适当的引用,指向要删除结点的子结点即可。

删除一个子结点的结点也有四种子情况:要删除结点的子结点可能是左子结点或右子结点,并且每种情况中的要删除结点也可能是自己父结点的左子结点或右子结点。还有一种特殊的情况:被删除结点可能是根,它没有父结点,只是被合适的子树所代替。下面是代码(从前面继续):
 View Code
View Code情况3:删除有两个子结点的结点
如果要删除的结点有两个子结点,就不能用它的一个子结点代替它,因为这样的话,如果子结点还有两个子结点,就会导致被替代的结点位置有3个子结点。

因此就需要另一种方法,幸运的是,这里有一种方法。我们知道二叉搜索树的结点是按照升序的关键字值排列的,对每一个结点来说,比该结点的关键字值次高的结点是它的中序后继,可以成为该结点的后继。上面图中30就是25的后继,也就是说一个结点的右子结点的左子结点就是该结点的后继(很绕口啊)。我们可以用这个中序后继来代替该结点。

怎么找后继结点呢?对人来说,可以很快地找到结点的后继,只要扫一眼树就可以找到比删除结点大的下一个节点并且找到其后继。但是计算机不能扫一眼就找到结点的后继,它需要你告诉它怎么做(又傻又呆吧)。
首先程序找到初始结点的右子结点,它的关键字值一定比初始结点大,然后转到初始结点的右子结点的左子结点那里。以此类推,顺着左子结点的路径一直往下找,这个路径上的最后一个左子结点就是初始结点的后继。 这个算法可以找到比初始结点关键值大的结点集合中最小的一个结点。如果初始结点的右子结点没有左子结点,那么这个右子结点本身就是后继。

 View Code
View Code