在这一章节的学习中,我们将要学习一个数据结构——二叉树(Binary Tree),和基于二叉树上的搜索算法。
在二叉树的搜索中,我们主要使用了分治法(Divide Conquer)来解决大部分的问题。之所以大部分二叉树的问题可以使用分治法,是因为二叉树这种数据结构,是一个天然就帮你做好了分治法中“分”这个步骤的结构。
本章节的先修内容有:
- 什么是递归(Recursion)—— 请回到第二章节中复习
- 递归(Recursion)、回溯(Backtracking)和搜索(Search)的联系和区别
- 分治法(Divide and Conquer)和遍历法(Traverse)的联系和区别
- 什么是结果类 ResultType,什么时候使用 ResultType
- 什么是二叉查找树(Binary Search Tree)
- 什么是平衡二叉树(Balanced Binary Tree)
本章节的补充内容有:
- Morris 算法:使用 O(1) 的额外空间复杂度对二叉树进行先序遍历(Preorder Traversal)
- 用非递归的方法实现先序遍历,中序遍历和后序遍历
- 二叉查找树(Binary Search Tree)的增删查改
- Java 自带的平衡排序二叉树 TreeMap / TreeSet 的介绍和面试中的应用
二叉树上的遍历法
定义
遍历(Traversal),顾名思义,就是通过某种顺序,一个一个访问一个数据结构中的元素。比如我们如果需要遍历一个数组,无非就是要么从前往后,要么从后往前遍历。但是对于一棵二叉树来说,他就有很多种方式进行遍历:
- 层序遍历(Level order)
- 先序遍历(Pre order)
- 中序遍历(In order)
- 后序遍历(Post order)
我们在之前的课程中,已经学习过了二叉树的层序遍历,也就是使用 BFS 算法来获得二叉树的分层信息。通过 BFS 获得的顺序我们也可以称之为 BFS Order。而剩下的三种遍历,都需要通过深度优先搜索的方式来获得。而这一小节中,我们将讲一下通过深度优先搜索(DFS)来获得的节点顺序,
先序遍历 / 中序遍历 / 后序遍历
先序遍历(又叫先根遍历、前序遍历)
首先访问根结点,然后遍历左子树,最后遍历右子树。遍历左、右子树时,仍按先序遍历。若二叉树为空则返回。
该过程可简记为根左右,注意该过程是递归的。如图先序遍历结果是:ABDECF。

1 // 将根作为root,空ArrayList作为result传入,即可得到整棵树的遍历结果 2 private void traverse(TreeNode root, ArrayList<Integer> result) { 3 if (root == null) { 4 return; 5 } 6 result.add(root.val); 7 traverse(root.left, result); 8 traverse(root.right, result); 9 }
中序遍历(又叫中根遍历)
首先遍历左子树,然后访问根结点,最后遍历右子树。遍历左、右子树时,仍按中序遍历。若二叉树为空则返回。简记为左根右。
上图中序遍历结果是:DBEAFC。
核心代码:
Java:

1 private void traverse(TreeNode root, ArrayList<Integer> result) { 2 if (root == null) { 3 return; 4 } 5 traverse(root.left, result); 6 result.add(root.val); // 注意访问根节点放到了遍历左子树的后面 7 traverse(root.right, result); 8 }
后序遍历(又叫后根遍历)
首先遍历左子树,然后遍历右子树,最后访问根结点。遍历左、右子树时,仍按后序遍历。若二叉树为空则返回。简记为左右根。
上图后序遍历结果是:DEBFCA。

1 private void traverse(TreeNode root, ArrayList<Integer> result) { 2 if (root == null) { 3 return; 4 } 5 traverse(root.left, result); 6 traverse(root.right, result); 7 result.add(root.val); // 注意访问根节点放到了最后 8 }
一些有趣的题目:
http://www.lintcode.com/problem/construct-binary-tree-from-inorder-and-postorder-traversal/
http://www.lintcode.com/problem/construct-binary-tree-from-preorder-and-inorder-traversal/
二叉树上的分治法
定义
分治法(Divide & Conquer Algorithm)是说将一个大问题,拆分为2个或者多个小问题,当小问题得到结果之后,合并他们的结果来得到大问题的结果。
举一个例子,比如中国要进行人口统计。那么如果使用遍历(Traversal)的办法,做法如下:
人口普查员小张自己一个人带着一个本子,跑遍全中国挨家挨户的敲门查户口
而如果使用分治法,做法如下:
- 国家统计局的老板小李想要知道全国人口的总数,于是他找来全国各个省的统计局领导,下派人口普查任务给他们,让他们各自去统计自己省的人口总数。在小李这儿,他只需要最后将各个省汇报的人口总数结果累加起来,就得到了全国人口的数目。
- 然后每个省的领导,又找来省里各个市的领导,让各个市去做人口统计。
- 市找县,县找镇,镇找乡。最后乡里的干部小王挨家挨户敲门去查户口。
在这里,把全国的任务拆分为省级的任务的过程,就是分治法中分的这个步骤。把各个小任务派发给别人去完成的过程,就是分治法中治的这个步骤。但是事实上我们还有第三个步骤,就是将小任务的结果合并到一起的过程,合这个步骤。因此如果我来取名字的话,我会叫这个算法:分治合算法。
为什么二叉树的问题适合使用分治法?
在一棵二叉树(Binary Tree)中,如果将整棵二叉树看做一个大问题的话,那么根节点(Root)的左子树(Left subtree)就是一个小问题,右子树(Right subtree)是另外一个小问题。这是一个天然就帮你完成了“分”这个步骤的数据结构。
二叉树的最大深度
判断平衡二叉树
判断二叉搜索树
递归,分治法,遍历法的联系与区别
联系
分治法(Divide & Conquer)与遍历法(Traverse)是两种常见的递归(Recursion)方法。
分治法解决问题的思路
先让左右子树去解决同样的问题,然后得到结果之后,再整合为整棵树的结果。
遍历法解决问题的思路
通过前序/中序/后序的某种遍历,游走整棵树,通过一个全局变量或者传递的参数来记录这个过程中所遇到的点和需要计算的结果。
两种方法的区别
从程序实现角度分治法的递归函数,通常有一个返回值,遍历法通常没有。
递归、回溯和搜索
什么是递归 (Recursion) ?
很多书上会把递归(Recursion)当作一种算法。事实上,递归是包含两个层面的意思的:
- 一种由大化小,由小化无的解决问题的算法。类似的算法还有动态规划(Dynamic Programming)。
- 一种程序的实现方式。这种方式就是一个函数(Function / Method / Procedure)自己调用自己。
与之对应的,有非递归(Non-Recursion)和迭代法(Iteration),你可以认为这两个概念是一样的概念(番茄和西红柿的区别)。不需要做区分。
什么是搜索 (Search)?
搜索分为深度优先搜索(Depth First Search)和宽度优先搜索(Breadth First Search),通常分别简写为 DFS 和 BFS。搜索是一种类似于枚举(Enumerate)的算法。比如我们需要找到一个数组里的最大值,我们可以采用枚举法,因为我们知道数组的范围和大小,比如经典的打擂台算法:
int max = nums[0]; for (int i = 1; i < nums.length; i++) { max = Math.max(max, nums[i]); }
枚举法通常是你知道循环的范围,然后可以用几重循环就搞定的算法。比如我需要找到 所有 x^2 + y^2 = K 的整数组合,可以用两重循环的枚举法:
// 不要在意这个算法的时间复杂度 for (int x = 1; x <= k; x++) { for (int y = 1; y <= k; y++) { if (x * x + y * y == k) { // print x and y } } }
而有的问题,比如求 N 个数的全排列,你可能需要用 N 重循环才能解决。这个时候,我们就倾向于采用递归的方式去实现这个变化的 N 重循环。这个时候,我们就把算法称之为搜索。因为你已经不能明确的写出一个不依赖于输入数据的多重循环了。
通常来说 DFS 我们会采用递归的方式实现(当然你强行写一个非递归的版本也是可以的),而 BFS 则无需递归(使用队列 Queue + 哈希表 HashMap就可以)。所以我们在面试中,如果一个问题既可以使用 DFS,又可以使用 BFS 的情况下,一定要优先使用 BFS。因为他是非递归的,而且更容易实现。
什么是回溯(Backtracking)?
有的时候,深度优先搜索算法(DFS),又被称之为回溯法,所以你可以完全认为回溯法,就是深度优先搜索算法。在我的理解中,回溯实际上是深度优先搜索过程中的一个步骤。比如我们在进行全子集问题的搜索时,假如当前的集合是 {1,2} 代表我正在寻找以 {1,2}开头的所有集合。那么他的下一步,会去寻找 {1,2,3}开头的所有集合,然后当我们找完所有以 {1,2,3} 开头的集合时,我们需要把 3 从集合中删掉,回到 {1,2}。然后再把 4 放进去,寻找以 {1,2,4} 开头的所有集合。这个把 3 删掉回到 {1,2} 的过程,就是回溯。
subset.add(nums[i]); subsetsHelper(result, subset, nums, i + 1); subset.remove(list.size() - 1) // 这一步就是回溯
详情请参考:
http://www.jiuzhang.com/solutions/subsets/
递归三要素
我们以《二叉树的最大深度》和《二叉树的前序遍历》两个题目为例子,来分析一下递归的三要素。
相关题目链接:
http://www.lintcode.com/problem/maximum-depth-of-binary-tree/
http://www.lintcode.com/problem/binary-tree-preorder-traversal/
1. 递归的定义
每一个递归函数,都需要有明确的定义,有了正确的定义以后,才能够对递归进行拆解。
例子:
Java:
int maxDepth(TreeNode root)
Python:
def maxDepth(root):
代表 以 root 开头的子树的最大深度是多少。
Java:
void preorder(TreeNode root, List<TreeNode> result)
Python:
def preorder(root, result):
代表 将 root 开头的子树的前序遍历放到 result 里面
2. 递归的拆解
一个
大问题如何拆解为若干个小问题去解决。
例子:
Java:
int leftDepth = maxDepth(root.left);
int rightDepth = maxDepth(root.right);
return Math.max(leftDepth, rightDepth) + 1;
Python:
leftDepth = maxDepth(root.left)
rightDepth = maxDepth(root.right)
return max(leftDepth, rightDepth) + 1
整棵树的最大深度,可以拆解为先计算左右子树深度,然后在左右子树深度中找到最大值+1来解决。
Java:
result.add(root);
preorder(root.left, result);
preorder(root.right, result);
Python:
result.append(root)
preorder(root.left, result)
perorder(root.right, result)
一棵树的前序遍历可以拆解为3个部分:
- 根节点自己(root)
- 左子树的前序遍历
- 右子树的前序遍历
所以对应的,我们把这个递归问题也拆分为三个部分来解决:
- 先把 root 放到 result 里 --> result.add(root);
- 再把左子树的前序遍历放到 result 里 --> preorder(root.left, result)。回想一下递归的定义,是不是正是如此?
- 再把右子树的前序遍历放到 result 里 --> preorder(root.right, result)。
3. 递归的出口
什么时候可以直接知道答案,不用再拆解,直接 return
例子:
Java:
// 二叉树的最大深度
if (root == null) {
return 0;
}
Python:
# 二叉树的最大深度
if not root:
return 0
一棵空的二叉树,可以认为是一个高度为0的二叉树。
Java:
// 二叉树的前序遍历
if (root == null) {
return;
}
Python:
if not root:
return
一棵空的二叉树,自然不用往 result 里放任何的东西。
递归的定义
每一个递归函数,都需要有明确的定义,有了正确的定义以后,才能够对递归进行拆解。
例子:
Java:
int maxDepth(TreeNode root)
Python:
def maxDepth(root):
代表 以 root 开头的子树的最大深度是多少。
Java:
void preorder(TreeNode root, List<TreeNode> result)
Python:
def preorder(root, result):
代表 将 root 开头的子树的前序遍历放到 result 里面
递归的拆解
一个
大问题如何拆解为若干个小问题去解决。
例子:
Java:
int leftDepth = maxDepth(root.left);
int rightDepth = maxDepth(root.right);
return Math.max(leftDepth, rightDepth) + 1;
Python:
leftDepth = maxDepth(root.left)
rightDepth = maxDepth(root.right)
return max(leftDepth, rightDepth) + 1
整棵树的最大深度,可以拆解为先计算左右子树深度,然后在左右子树深度中找到最大值+1来解决。
Java:
result.add(root);
preorder(root.left, result);
preorder(root.right, result);
Python:
result.append(root)
preorder(root.left, result)
preorder(root.right, result)
一棵树的前序遍历可以拆解为3个部分:
- 根节点自己(root)
- 左子树的前序遍历
- 右子树的前序遍历
所以对应的,我们把这个递归问题也拆分为三个部分来解决:
- 先把 root 放到 result 里 --> result.add(root);
- 再把左子树的前序遍历放到 result 里 --> preorder(root.left, result)。回想一下递归的定义,是不是正是如此?
- 再把右子树的前序遍历放到 result 里 --> preorder(root.right, result)。
递归的出口
什么时候可以直接知道答案,不用再拆解,直接 return
例子:
Java:
// 二叉树的最大深度
if (root == null) {
return 0;
}
Python:
# 二叉树的最大深度
if not root:
return 0
一棵空的二叉树,可以认为是一个高度为0的二叉树。
Java:
// 二叉树的前序遍历
if (root == null) {
return;
}
Python:
if not root:
return
一棵空的二叉树,自然不用往 result 里放任何的东西。
使用 ResultType 返回多个值
什么是 ResultType
通常是我们定义在某个文件内部使用的一个类。比如:
Java:
class ResultType {
int maxValue, minValue;
public ResultType(int maxValue, int minValue) {
this.maxValue = maxValue;
this.minValue = minValue;
}
}
什么时候需要 ResultType
当我们定义的函数需要返回多个值供调用者计算时,就需要使用 ResultType了。
所以如果你只是返回一个值就够用的话,就不需要。
其他语言需要 ResulType 么?
不是所有的语言都需要自定义 ResultType。
像 Python 这样的语言,天生支持你返回多个值作为函数的 return value,所以是不需要的。
什么是二叉搜索树
定义
二叉搜索树(Binary Search Tree,又名排序二叉树,二叉查找树,通常简写为BST)定义如下:
空树或是具有下列性质的二叉树:
(1)若左子树不空,则左子树上所有节点值均小于或等于它的根节点值;
(2)若右子树不空,则右子树上所有节点值均大于根节点值;
(3)左、右子树也为二叉搜索树;
如图即为BST:
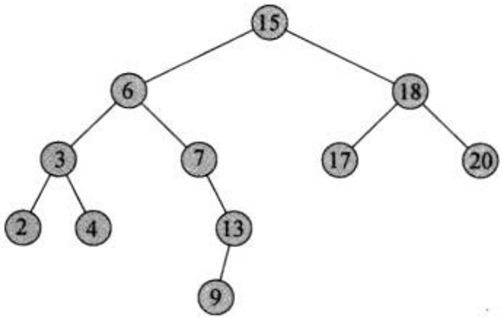
BST 的特性
- 按照中序遍历(inorder traversal)打印各节点,会得到由小到大的顺序。
- 在BST中搜索某值的平均情况下复杂度为O(logN)O(logN)O(logN),最坏情况下复杂度为O(N)O(N)O(N),其中N为节点个数。将待寻值与节点值比较,若不相等,则通过是小于还是大于,可断定该值只可能在左子树还是右子树,继续向该子树搜索。
- 在balanced BST中查找某值的时间复杂度为O(logN)O(logN)O(logN)。
BST 的作用
- 通过中序遍历,可快速得到升序节点列表。
- 在BST中查找元素,平均情况下时间复杂度是O(logN)O(logN)O(logN);插入新节点,保持BST特性平均情况下要耗时O(logN)。(参考链接)。
- 和有序数组的对比:有序数组查找某元素可以用二分法,时间复杂度是O(logN);但是插入新元素,维护数组有序性要耗时O(N)。
常见的BST面试题
http://www.lintcode.com/en/tag/binary-search-tree/
BST是一种重要且基本的结构,其相关题目也十分经典,并延伸出很多算法。
在BST之上,有许多高级且有趣的变种,以解决各式各样的问题,例如:
什么是平衡二叉搜索树
定义
平衡二叉搜索树(Balanced Binary Search Tree,又称为AVL树,有别于AVL算法)是二叉树中的一种特殊的形态。二叉树当且仅当满足如下两个条件之一,是平衡二叉树:
- 空树。
- 左右子树高度差绝对值不超过1且左右子树都是平衡二叉树。
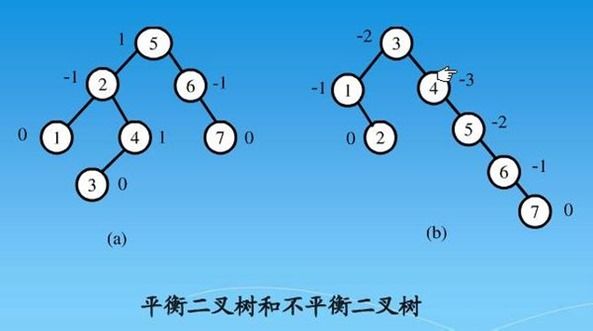
如图(图片来自网络),节点旁边的数字表示左右两子树高度差。(a)是AVL树,(b)不是,(b)中5节点不满足AVL树,故4节点,3节点都不再是AVL树。
AVL树的高度为 O(logN)O(logN)O(logN)
当AVL树有N个节点时,高度为O(logN)O(logN)O(logN)。为何?
试想一棵满二叉树,每个节点左右子树高度相同,随着树高的增加,叶子容量指数暴增,故树高一定是O(logN)O(logN)O(logN)。而相比于满二叉树,AVL树仅放宽一个条件,允许左右两子树高度差1,当树高足够大时,可以把1忽略。如图是高度为9的最小AVL树,若节点更少,树高绝不会超过8,也即为何AVL树高会被限制到O(logN)O(logN)O(logN),因为树不可能太稀疏。严格的数学证明复杂,略去。
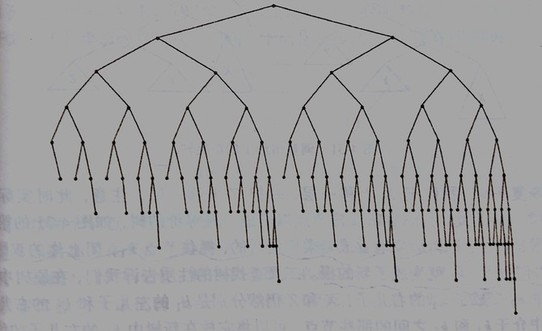
为何普通二叉树不是O(logN)O(logN)O(logN)?这里给出最坏的单枝树,若单枝扩展,则树高为O(N)O(N)O(N):
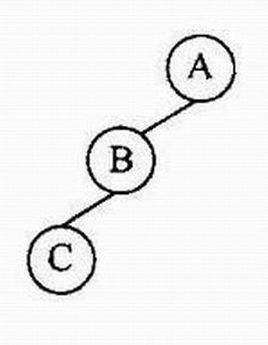
AVL树有什么用?
最大作用是保证查找的最坏时间复杂度为O(logN)。而且较浅的树对插入和删除等操作也更快。
AVL树的相关练习题
判断一棵树是否为平衡树
http://www.lintcode.com/problem/balanced-binary-tree/
提示:可以自下而上递归判断每个节点是否平衡。若平衡将当前节点高度返回,供父节点判断;否则该树一定不平衡。
补充内容:
用 Morris 算法实现 O(1) 额外空间遍历二叉树
https://www.jiuzhang.com/tutorial/algorithm/402
非递归的方式实现二叉树遍历
先序遍历
思路
遍历顺序为根、左、右
- 如果根节点非空,将根节点加入到栈中。
- 如果栈不空,弹出出栈顶节点,将其值加加入到数组中。
- 如果该节点的右子树不为空,将右子节点加入栈中。
- 如果左子节点不为空,将左子节点加入栈中。
- 重复第二步,直到栈空。
练习
http://www.lintcode.com/problem/binary-tree-preorder-traversal/
public class Solution { public List<Integer> preorderTraversal(TreeNode root) { Stack<TreeNode> stack = new Stack<TreeNode>(); List<Integer> preorder = new ArrayList<Integer>(); if (root == null) { return preorder; } stack.push(root); while (!stack.empty()) { TreeNode node = stack.pop(); preorder.add(node.val); if (node.right != null) { stack.push(node.right); } if (node.left != null) { stack.push(node.left); } } return preorder; } }
中序遍历
思路
遍历顺序为左、根、右
- 如果根节点非空,将根节点加入到栈中。
- 如果栈不空,取栈顶元素(暂时不弹出),
- 如果左子树已访问过,或者左子树为空,则弹出栈顶节点,将其值加入数组,如有右子树,将右子节点加入栈中。
- 如果左子树不为空,则将左子节点加入栈中。
- 重复第二步,直到栈空。
练习
http://www.lintcode.com/problem/binary-tree-inorder-traversal/
public class Solution { /** * @param root: The root of binary tree. * @return: Inorder in ArrayList which contains node values. */ public ArrayList<Integer> inorderTraversal(TreeNode root) { Stack<TreeNode> stack = new Stack<>(); ArrayList<Integer> result = new ArrayList<>(); while (root != null) { stack.push(root); root = root.left; } while (!stack.isEmpty()) { TreeNode node = stack.peek(); result.add(node.val); if (node.right == null) { node = stack.pop(); while (!stack.isEmpty() && stack.peek().right == node) { node = stack.pop(); } } else { node = node.right; while (node != null) { stack.push(node); node = node.left; } } } return result; } }
后序遍历
思路
遍历顺序为左、右、根
- 如果根节点非空,将根节点加入到栈中。
- 如果栈不空,取栈顶元素(暂时不弹出),
- 如果(左子树已访问过或者左子树为空),且(右子树已访问过或右子树为空),则弹出栈顶节点,将其值加入数组,
- 如果左子树不为空,切未访问过,则将左子节点加入栈中,并标左子树已访问过。
- 如果右子树不为空,切未访问过,则将右子节点加入栈中,并标右子树已访问过。
- 重复第二步,直到栈空。
练习
http://www.lintcode.com/problem/binary-tree-postorder-traversal/
public ArrayList<Integer> postorderTraversal(TreeNode root) { ArrayList<Integer> result = new ArrayList<Integer>(); Stack<TreeNode> stack = new Stack<TreeNode>(); TreeNode prev = null; // previously traversed node TreeNode curr = root; if (root == null) { return result; } stack.push(root); while (!stack.empty()) { curr = stack.peek(); if (prev == null || prev.left == curr || prev.right == curr) { // traverse down the tree if (curr.left != null) { stack.push(curr.left); } else if (curr.right != null) { stack.push(curr.right); } } else if (curr.left == prev) { // traverse up the tree from the left if (curr.right != null) { stack.push(curr.right); } } else { // traverse up the tree from the right result.add(curr.val); stack.pop(); } prev = curr; } return result; }
什么是二叉搜索树(Binary Search Tree)
二叉搜索树可以是一棵空树或者是一棵满足下列条件的二叉树:
- 如果它的左子树不空,则左子树上所有节点值
均小于它的根节点值。 - 如果它的右子树不空,则右子树上所有节点值
均大于它的根节点值。 - 它的左右子树均为二叉搜索树(BST)。
- 严格定义下BST中是没有值相等的节点的(No duplicate nodes)。
根据上述特性,我们可以得到一个结论:BST中序遍历得到的序列是升序的。如下述BST的中序序列为:[1,3,4,6,7,8,10,13,14]
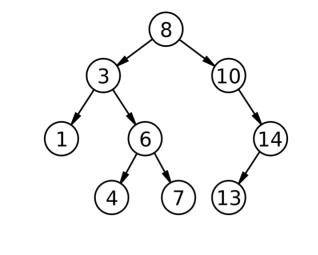
BST基本操作——增删改查(CRUD)
https://www.jiuzhang.com/tutorial/algorithm/401
平衡排序二叉树(Self-balancing Binary Search Tree)
定义
平衡二叉搜索树又被称为AVL树(有别于AVL算法),且具有以下性质:
- 它是一棵空树或它的左右两个子树的高度差的绝对值不超过1
- 左右两棵子树都是一棵平衡二叉搜索树
- 平衡二叉搜索树必定是二叉搜索树,反之则不一定。
平衡排序二叉树 与 二叉搜索树 对比
也许因为输入值不够随机,也许因为输入顺序的原因,还或许一些插入、删除操作,会使得二叉搜索树失去平衡,造成搜索效率低落的情况。
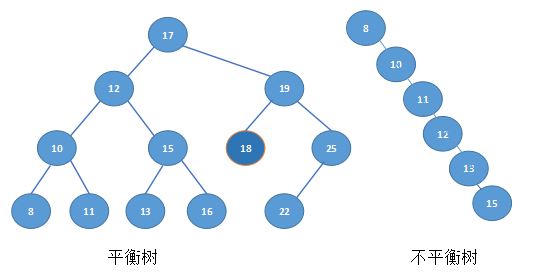
比如上面两个树,在平衡树上寻找15就只要2次查找,在非平衡树上却要5次查找方能找到,效率明显下降。
平衡排序二叉树节点定义
Java:
class TreeNode{
int val;
TreeNode left;
TreeNode right;
pubic TreeNode(int val) {
this.val = val;
this.left = this.right = null;
}
}
Python:
class TreeNode:
def __init__(self, val):
self.val = val
self.left, self.right = None, None
常用的实现办法
- AVL树 --> https://en.wikipedia.org/wiki/AVL_tree
- 红黑树(Red Black Tree) --> http://blog.csdn.net/v_july_v/article/details/6105630
Java中的 TreeSet / TreeMap
TreeSet / TreeMap 是底层运用了红黑树的数据结构
对比 HashSet / HashMap
- HashSet / HashMap 存取的时间复杂度为O(1),而 TreeSet / TreeMap 存取的时间复杂度为 O(logn) 所以在存取上并不占优。
- HashSet / HashMap 内元素是无序的,而TreeSet / TreeMap 内部是有序的(可以是按自然顺序排列也可以自定义排序)。
- TreeSet / TreeMap 还提供了类似 lowerBound 和 upperBound 这两个其他数据结构没有的方法
- 对于 TreeSet, 实现上述两个方法的方法为:
- lowerBound
- public E lower(E e) --> 返回set中严格小于给出元素的最大元素,如果没有满足条件的元素则返回 null。
- public E floor(E e) --> 返回set中不大于给出元素的最大元素,如果没有满足条件的元素则返回 null。
- upperBound
- public E higher(E e) --> 返回set中严格大于给出元素的最小元素,如果没有满足条件的元素则返回 null。
- public E ceiling(E e) --> 返回set中不小于给出元素的最小元素,如果没有满足条件的元素则返回 null。
- lowerBound
- 对于 TreeMap, 实现上述两个方法的方法为:
- lowerBound
- public Map.Entry<K,V> lowerEntry(K key) --> 返回map中严格小于给出的key值的最大key对应的key-value对,如果没有满足条件的key则返回 null。
- public K lowerKey(K key) --> 返回map中严格小于给出的key值的最大key,如果没有满足条件的key则返回 null。
- public Map.Entry<K,V> floorEntry(K key) --> 返回map中不大于给出的key值的最大key对应的key-value对,如果没有满足条件的key则返回 null。
- public K floorKey(K key) --> 返回map中不大于给出的key值的最大key,如果没有满足条件的key则返回 null。
- upperBound
- public Map.Entry<K,V> higherEntry(K key) --> 返回map中严格大于给出的key值的最小key对应的key-value对,如果没有满足条件的key则返回 null。
- public K higherKey(K key) --> 返回map中严格大于给出的key值的最小key,如果没有满足条件的key则返回 null。
- public Map.Entry<K,V> ceilingEntry(K key) --> 返回map中不小于给出的key值的最小key对应的key-value对,如果没有满足条件的key则返回 null。
- public K ceilingKey(K key) --> 返回map中不小于给出的key值的最小key,如果没有满足条件的key则返回 null。
- lowerBound
- lowerBound 与 upperBound 均为二分查找(因此要求有序),时间复杂度为O(logn).
- 对于 TreeSet, 实现上述两个方法的方法为:
对比 PriorityQueue(Heap)
PriorityQueue是基于Heap实现的,它可以保证队头元素是优先级最高的元素,但其余元素是不保证有序的。
- 方法时间复杂度对比:
- 添加元素 add() / offer()
- TreeSet: O(logn)
- PriorityQueue: O(logn)
- 删除元素 poll() / remove()
- TreeSet: O(logn)
- PriorityQueue: O(n)
- 查找 contains()
- TreeSet: O(logn)
- PriorityQueue: O(n)
- 取最小值 first() / peek()
- TreeSet: O(logn)
- PriorityQueue: O(1)
- 添加元素 add() / offer()
常见用法
比如滑动窗口需要保证有序,那么这时可以用到TreeSet,因为TreeSet是有序的,并且不需要每次移动窗口都重新排序,只需要插入和删除(O(logn))就可以了。
注:在 C++ 中类似的结构为 set / map。在Python中没有内置的TreeSet、TreeMap,需要使用第三方库或者自己实现。
练习
http://www.lintcode.com/problem/consistent-hashing-ii/
练习:链表转平衡排序二叉树
https://www.jiuzhang.com/tutorial/algorithm/33
