深度缓冲,做图形的朋友应该不会陌生。一般来说我们通过深度缓冲来确定一个像素是否比另一个像素离摄像机更远。在图形学中,我们一般使用三次空间变换,来将模型坐标系下的物体坐标,转换到clip space下(x : -1 ~ 1, y: -1 ~ 1, z -1 ~ 1),然后最后再将clip space计算得来的图形变换到屏幕像素空间。
要说非线性深度之前,我们先说说线性深度,所谓线性,就是指变化曲线的一阶导数为常量,也就是说变化量是恒定的。既然变换是恒定的,那么深度z的采样点在-1~ 1之间就是均匀分布。在做延迟渲染时,我们一般需要这种深度,以避免深度采样点分布不均匀时,在某一区间内由深度计算出的空间位置误差太大。相反之,非线性深度就是指曲线一阶导数不为常量,曲线的变化量并非恒定,当然在这种情况下,采样点的分布也自然是不均匀的。图形在进行三次变换后,计算出来的深度就是非线性的,基本上可以概括为摄像机近处深度的精度高,远处深度精度低。为什么会有这样的结果呢?其实对深度影响最大的是三次变换中的透视变换,要知道为什么,就必须先搞定透视变换的原理。
透视变换的目的就是将坐标由camera空间变换到clip空间,其主要使用了数学上三角形相似定理,线性插值和三角函数。这里概述一下:


要将p通过矩阵变换到p’,需要借助于齐次坐标,因为 1/z 与 z非线性相关,所以不能通过线性变换由z 得到 1/z。因此p’可以表示为齐次坐标(Nx,Ny,z,-z)。这个公式还是存在问题,就是z /w后等于-1(w=-z),这样一来在变换后,z的信息并没有保存下来。怎么解决这个问题?这里用到了一个数学技巧:将z写成az + b,这样一来z / w = -a – b / z,这样z的信息就保存下来了。
那么变换后的f(z)可以简化为1/z的函数,很明显这个函数不是线性函数。我们看看这个函数的图形:
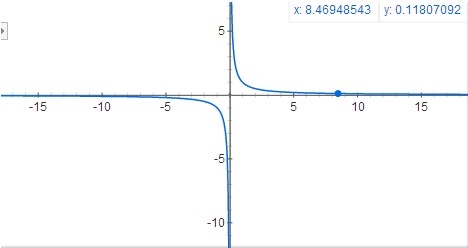
可以看到,当z很小时,f(z)的取值域很大,z较大后f(z)的取值域非常小。这说明了近处的物体z变化很更加敏感,精度更高。
http://blog.csdn.net/popy007/article/details/1797121
http://www.humus.name/index.php?page=News&ID=255
http://www.gamedev.net/topic/539378-why-non-linear-depth-buffer/