目标检测中焦点损失的入门指南！

作者|GUEST BLOG
编译|Flin
来源|analyticsvidhya

介绍

对象检测是计算机视觉社区中研究最广泛的主题之一。它已经进入了各个行业，涉及从图像安全，监视，自动车辆系统到机器检查的用例。

当前，基于深度学习的对象检测可以大致分为两类：

1. 两级检测器，例如基于区域的CNN（R-CNN）及其后续产品。

2. 一级探测器，例如YOLO系列探测器和SSD

应用于锚框的常规，密集采样（可能的物体位置）的一级检测器可能会更快，更简单，但由于在训练过程中遇到极端的等级失衡，其精度已经落后于两级探测器。

FAIR在2018年发表了一篇论文，其中他们引入了焦点损失的概念，用他们称为RetinaNet的一级探测器来处理此类不平衡问题。

在我们深入探讨焦点丢失的本质之前，让我们首先了解这个类不平衡问题是什么以及它可能引起的问题。

目录

1. 为什么需要焦点损失

2. 什么是焦点损失

3. 交叉熵损失

   1. 交叉熵问题
   2. 例子

4. 平衡交叉熵损失

   1. 平衡交叉熵问题
   2. 例子

5. 焦点损失说明

   1. 例子

6. 交叉熵损失 vs 焦点损失

   1. 容易正确分类的记录
   2. 分类错误的记录
   3. 非常容易分类的记录

7. 最后的想法

为什么需要焦点损失

两种经典的一级检测方法，如增强型检测器，DPM和最新的方法（如SSD）都可以评估每个图像大约10^4 至 10^5个候选位置，但只有少数位置包含对象（即前景），而其余只是背景对象。这导致了类不平衡的问题。

这种不平衡导致两个问题

1. 训练效率低下，因为大多数位置都容易被判断为负类（这意味着检测器可以轻松将其归类为背景），这对检测器的学习没有帮助。

2. 容易产生的负类（概率较高的检测）占输入的很大一部分。虽然单独计算的梯度和损失较小，但它们可能使损耗和计算出的梯度不堪重负，并可能导致模型退化。

什么是焦点损失

简而言之，焦点损失（Focal Loss，FL）是交叉熵损失（Cross-Entropy Loss，CE）的改进版本，它通过为难分类的或容易错误分类的示例（即带有噪声纹理的背景或部分对象的或我们感兴趣的对象）分配更多的权重来处理类不平衡问题，并对简单示例（即背景对象）降低权重。

因此，焦点损失减少了简单示例的损失贡献，并加强了对纠正错误分类的示例的重视。

因此，让我们首先了解二进制分类的交叉熵损失。

交叉熵损失

交叉熵损失背后的思想是惩罚错误的预测，而不是奖励正确的预测。

二进制分类的交叉熵损失如下：

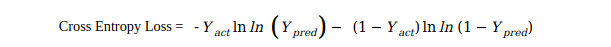
其中：

Y_act = Y的实际值

Y_pred = Y的预测值

为了标记方便，我们记 Y_act = Y 且 Y_pred = p 。

Y∈{0,1}，这是正确标注

p∈[0,1]，是模型对Y = 1的类别的估计概率。

为了符号上的方便，我们可以将上述方程式改写为：

p_t = {-ln(p) ,当Y=1 -ln(1-p) ,当 Y=}

CE（p，y）= CE（p_t）=-ln⁡（p_t）

交叉熵问题

如你所见，下图中的蓝线表示当p非常接近0（当Y = 0时）或1时，容易分类的p_t > 0.5的示例可能会产生不小的幅度的损失。

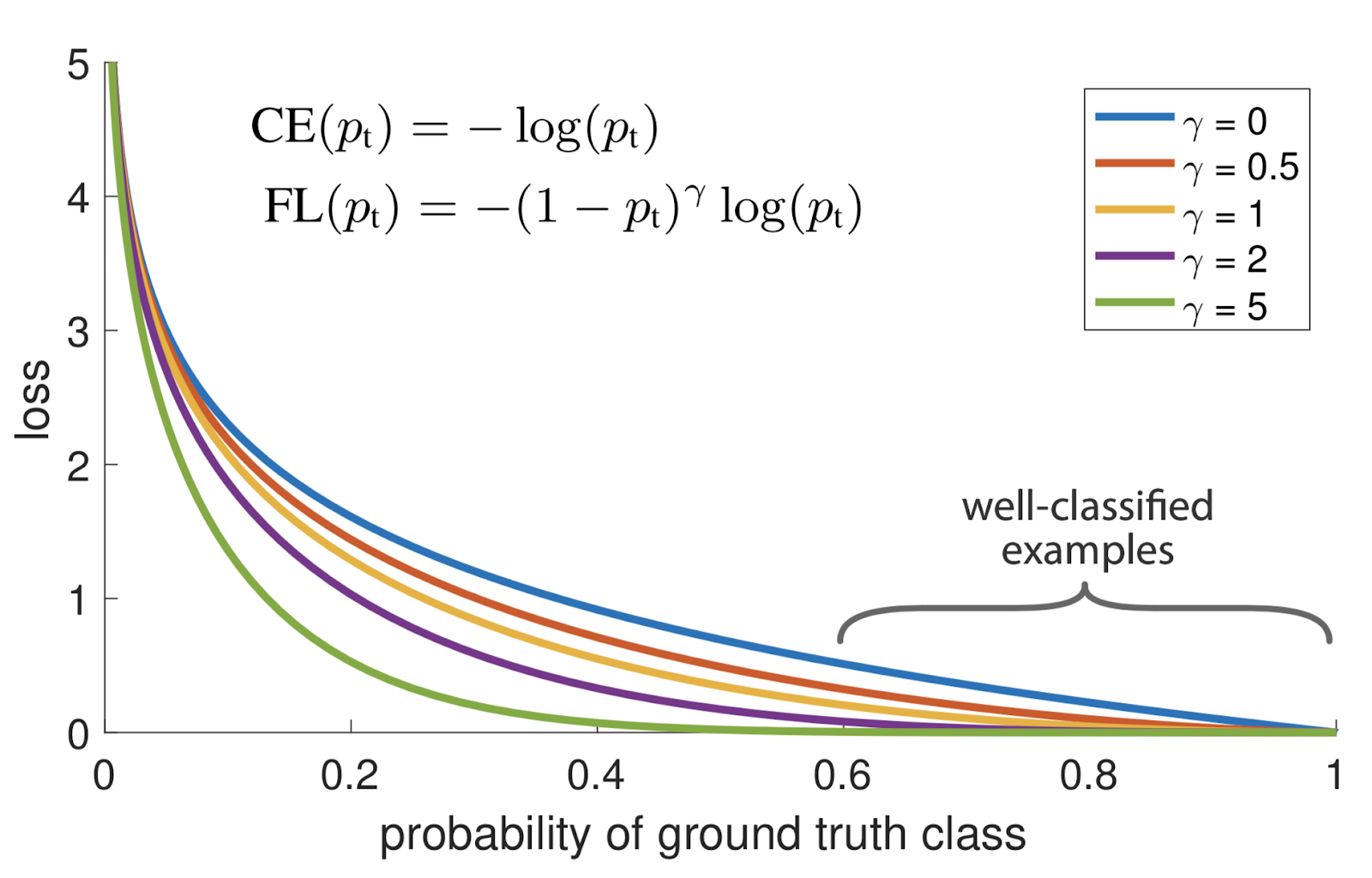
让我们用下面的例子来理解它。

例子

假设，前景（我们称其为类1）正确分类为p = 0.95 ——

CE（FG）= -ln（0.95）= 0.05

并且背景（我们称其为类0）正确分类为p = 0.05 ——

CE（BG）=-ln（1- 0.05）= 0.05

问题是，对于类不平衡的数据集，当这些小的损失在整个图像上相加时，可能会使整体损失（总损失）不堪重负。因此，将导致模型退化。

平衡交叉熵损失

解决类别不平衡问题的一种常见方法是为类别引入权重因子∝[0,1]

为了标记方便，我们可以在损失函数中定义 ∝_t 如下：

CE（p_t）= -∝_t ln ln（p_t）

如你所见，这只是交叉熵的扩展。

平衡交叉熵的问题

我们的实验将表明，在密集检测器训练过程中遇到的大类不平衡压倒了交叉熵损失。

容易分类的负类占损耗的大部分，并主导梯度。虽然平衡了正例/负例的重要性，但它并没有区分简单/困难的示例。

让我们通过一个例子来理解这一点

例子

假设，前景（我们称其为类1）正确分类为p = 0.95 ——

CE（FG）= -0.25 * ln（0.95）= 0.0128

正确分类为p = 0.05的背景（我们称之为类0）——

CE（BG）=-（1-0.25）* ln（1- 0.05）= 0.038

虽然可以很好地正确区分正类和负类，但仍然不能区分简单/困难的例子。

这就是焦点损失（扩展到交叉熵）起作用的地方。

焦点损失说明

焦点损失只是交叉熵损失函数的扩展，它将降低简单示例的权重，并将训练重点放在困难的负样本上。

为此，研究人员提出：
（1- p_t）^γ 为交叉熵损失，且可调聚焦参数γ≥0。

RetinaNet物体检测方法使用焦点损失的α平衡变体，其中α = 0.25，γ= 2效果最佳。

因此，焦点损失可以定义为——

FL (p_t) = -α_t(1- p_t)^γ log log(p_t).

对于γ∈[0,5]的几个值，可以看到焦点损失，请参见图1。

我们将注意到焦点损失的以下特性：

1. 当示例分类错误并且p_t小时，调制因数接近1，并且损失不受影响。
2. 当 p_t →1 时，该因子变为0，并且对分类良好的示例的损失进行了权衡。
3. 聚焦参数γ平滑地调整了简单示例的权重。

随着增加，调制因数的作用同样增加。（经过大量实验和试验，研究人员发现γ = 2效果最佳）

注意：当γ= 0时，FL等效于CE。参考图中蓝色曲线。

直观上，调制因数减少了简单示例的损耗贡献，并扩展了示例接收低损耗的范围。

让我们通过一个例子来了解上述焦点损失的特性。

例子

• 当记录（前景或背景）被正确分类时，

1. 前景正确分类，预测概率p=0.99，背景正确分类，预测概率p=0.01。

   p_t = {0.99，当Y_act = 1 时 1-0.01，当Y _act = 0时}调制因数（FG）=（1-0.99）² = 0.0001
   调制因数（BG）=（1-（1-0.01））2 = 0.0001,如你所见，调制因数接近于0，因此损耗将被权重降低。

2. 前景被错误分类，预测概率p = 0.01，背景对象被错误分类，预测概率p = 0.99。
   p_t = {0.01，当Y_act = 1 时 1-0.99，当Y _act = 0时}调制因数（FG）=（1-0.01）² = 0.9801
   调制因数（BG）=（1-（1-0.99））² = 0.9801如你所见，调制因数接近于1，因此损耗不受影响。

现在，让我们使用一些示例比较交叉熵和焦点损失，并查看焦点损失在训练过程中的影响。

交叉熵损失 vs 焦点损失

让我们通过考虑以下几种情况来进行比较。

容易正确分类的记录

假设前景正确分类的预测概率为p = 0.95，背景正确分类的背景为预测概率p = 0.05。
p_t = {0.95, 当 Y_act=1时 1-0.05 ,当 Y_act = 0时} CE(FG)= -ln (0.95) = 0.0512932943875505

让我们考虑在∝ = 0.25和γ= 2时的焦点损失。

FL(FG)= -0.25 * (1-0.95)² * ln (0.95) = 3.2058308992219E-5

FL(BG)= -0.75 * (1-(1-0.05))² * ln (1-0.05) = 9.61E-5

分类错误的记录

假设预测概率p=0.05的前景被分类为预测概率p=0.05的背景对象。

p_t = {0.95，当Y act = 1 1-0.05时，当Y act = 0时}

CE（FG）= -ln（0.05）= 2.995732273553991

CE（BG）= -ln（1-0.95）= 2.995732273553992

让我们考虑相同的场景，即∞=0.25和γ=2。

FL（FG）= -0.25 * （1-0.05）2 * ln（0.05）= 0.675912094220619
FL（BG）= -0.75 * （1-（1-0.95））2 * ln（1-0.95）= 2.027736282661858

非常容易分类的记录

假设对预测概率p=0.01的背景对象，用预测概率p=0.99对前景进行分类。

p_t = {0.99, 当 Y_act=1时 1-0.01 ,当 Y_act = 0时}CE(FG)= -ln (0.99) = 0.0100503358535014

CE（BG）= -ln（1-0.01）= 0.0100503358535014

让我们考虑相同的场景，即∞=0.25和γ=2。

FL（FG）= -0.25 * （1-0.01）2 * ln（0.99）= 2.51 * 10 -7
FL（BG）= -0.75 * （1-（1-0.01））2 * ln（1-0.01） = 7.5377518901261E-7

最后的想法

方案1：0.05129 / 3.2058 * 10 -7 =小1600倍
方案2：2.3 / 0.667 =小4.5倍
方案3：0.01 / 0.00000025 =小40,000倍。

这三个案例清楚地说明了焦点损失如何减小分类良好的记录的权重，另一方面又为错误分类或较难分类的记录赋予较大的权重。

经过大量的试验和实验，研究人员发现 ∝ = 0.25和 γ = 2 效果最佳。

尾注

在对象检测中，我们经历了从交叉熵损失到焦点损失的整个进化过程。我已经尽力解释了目标检测中的焦点损失。

感谢阅读！

参考

• https://arxiv.org/ftp/arxiv/papers/2006/2006.01413.pdf

• https://medium.com/@14prakash/the-intuition-behind-retinanet-eb636755607d

• https://developers.arcgis.com/python / guide / how-retinanet-works /

原文链接：https://www.analyticsvidhya.com/blog/2020/08/a-beginners-guide-to-focal-loss-in-object-detection/

欢迎关注磐创AI博客站：
http://panchuang.net/

sklearn机器学习中文官方文档：
http://sklearn123.com/

欢迎关注磐创博客资源汇总站：
http://docs.panchuang.net/