概念
二叉树:
树中每个节点最多有两个;
二叉搜索树:
1.若任意结点的左子树不空,则左子树上所有结点的值均不大于它的根结点的值。
2. 若任意结点的右子树不空,则右子树上所有结点的值均不小于它的根结点的值。
3.任意结点的左、右子树也分别为二叉搜索树。
二叉排序树:
1. 若它的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
2. 若它的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
3. 它的左右子树也分别为二叉排序树。
二叉查找树:
又称二叉排序树;以根节点为中心,左边的都比它小,右边的都比它大;
平衡二叉树:
是二叉排序树的改进版;
它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树
满二叉树:
树中所有的叶子节点都在同一层,每个节点都有两个子节点(每一层节点数达到最大值)
完全二叉树:
满足满二叉树的前提下,最后一层叶子均在最左边;(完全二叉树不是满二叉树, 满二叉树是完全二叉树)
二叉树的遍历

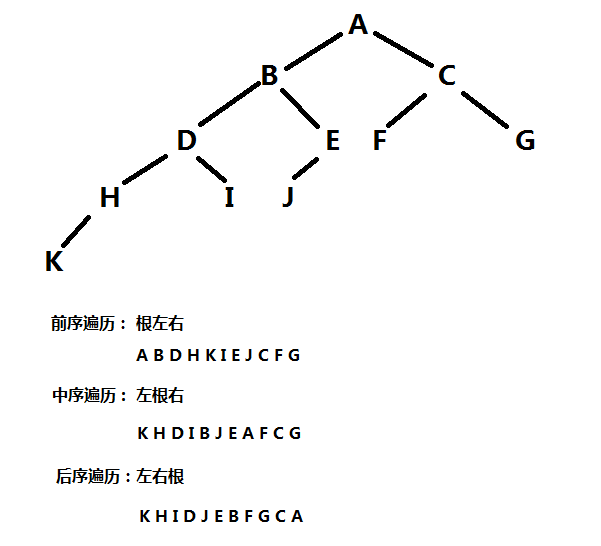
完整代码
#include <stdio.h>
#include <stdlib.h>
typedef struct tNode
{
char data;
struct tNode * lson; // 左孩子
struct tNode * rson; // 右孩子
}tNode;
// 创建树即创建根节点
tNode * CreateNode (char data)
{
tNode * tree = (tNode *) malloc (sizeof(tNode));
tree->data = data;
tree->lson = NULL;
tree->rson = NULL;
return tree;
}
// 连接节点, 将没有规律的树连接起来
void InsertNode(tNode * curNode, tNode * lNode, tNode * rNode)
{
curNode->lson = lNode;
curNode->rson = rNode;
}
// 递归遍历,每个节点打印出来
// 打印表示遍历, 打印当前节点数据
void PrintData(tNode * curNode)
{
printf("%c ", curNode->data);
}
// 先序
void PreOrder(tNode * curNode)
{
if (curNode == NULL) return;
PrintData(curNode);
PreOrder(curNode->lson);
PreOrder(curNode->rson);
}
// 中序
void MidOrder(tNode * curNode)
{
if (curNode == NULL) return;
MidOrder(curNode->lson);
PrintData(curNode);
MidOrder(curNode->rson);
}
// 后序
void EndOrder(tNode * curNode)
{
if (curNode == NULL) return;
EndOrder(curNode->lson);
PrintData(curNode);
EndOrder(curNode->rson);
}
int main()
{
// 创建树,此时还是乱的
tNode * A = CreateNode('A');
tNode * B = CreateNode('B');
tNode * C = CreateNode('C');
tNode * D = CreateNode('D');
tNode * E = CreateNode('E');
tNode * F = CreateNode('F');
tNode * G = CreateNode('G');
tNode * H = CreateNode('H');
tNode * I = CreateNode('I');
tNode * J = CreateNode('J');
tNode * K = CreateNode('K');
// 连接树
InsertNode(A, B, C);
InsertNode(B, D, E);
InsertNode(C, F, G);
InsertNode(D, H, I);
InsertNode(H, K, NULL);
InsertNode(E, J, NULL);
printf("前序遍历: ");
PreOrder(A);
printf("
");
printf("中序遍历: ");
MidOrder(A);
printf("
");
printf("后序遍历: ");
EndOrder(A);
printf("
");
}
