【转】图的 最小生成树算法 原理简介：Prim’s algorithm

转，原文：https://blog.csdn.net/qq_31534103/article/details/88809762

----------------------

文章目录

• Graph
• • Minimum Spanning Tree（最小生成树)）
  • • 生成算法
    • • 1. Prim's algorithm（ 普林演算法 ）
      • • 实现
        • 与 Dijkstra 的差异
      • 2.Kruskal's algorithm（克鲁斯卡尔算法）
      • • 实现

Graph

Minimum Spanning Tree（最小生成树)）

定义：For an undirected graph G，is a tree formed from graph edges that：
① connects all the vertices of G ② at lowest total cost.

存在性：MST exists iff G is connected.

graph G	MST

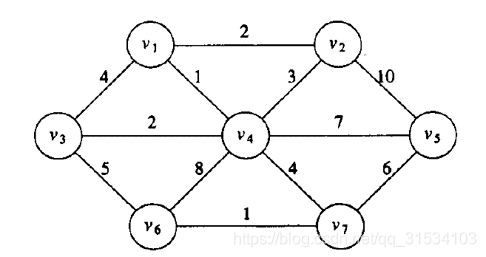生成算法

	Prim’s algorithm（ 普林演算法 ）	Kruskal’s algorithm（克鲁斯卡尔算法）
定义	首先以某一節點當作出發點，加入到树 T 内。 LOOP：在与树 T 邻接的树外（尚未被選取的）节点 E 中，选择到树 T 的边权重最小的节点 e， 將 e 和相应边加入 T。 UNTIL：增加了n - 1條邊為止。(假設有 n 個節點)	首先边的权重从小到大排序。 依次判断是否需要该边。要求加入该边后不会形成回路。
特性	贪心算法（局部最优） 不断扩张某一棵树	贪心算法（资源排序） 最开始所有点都看成是树，其过程就是不断连接森林里面的各棵树 •maintains a forest—a collection of trees.  •Initially, there are single-node trees. Adding an edge merges two trees into one.  •When the algorithm terminates, there is only one tree.

1. Prim’s algorithm（ 普林演算法 ）

实现

下表中，known 标志树内外节点 ，dv 标记该节点到树 T 的最小边权重，pv 记录其父节点。

1. 将节点 v1 作为 root 加入到树 T 中，更新邻接的树外点到树 T 的距离，即 v2、3、4 到 v1 的边权重。

   选择邻接边中权重最小的节点 v4 将其加入到 T 中，即：将 known（v4）= T，pv（v4）= v1。

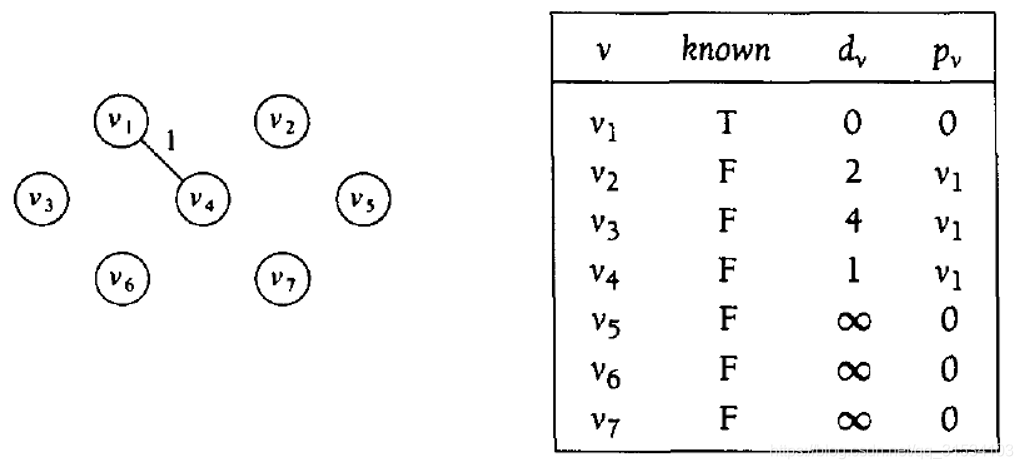
2. 重复：将 v2 加入到 T 中，更新邻接于 v4 的树外点到树 T 的距离，例如 v3 与 v2 的距离比 v1 更近，所以dv（v3）= 2，pv（v3）= v2。

   选择邻接边中权重最小的节点 v2、3 将其加入到 T 中。

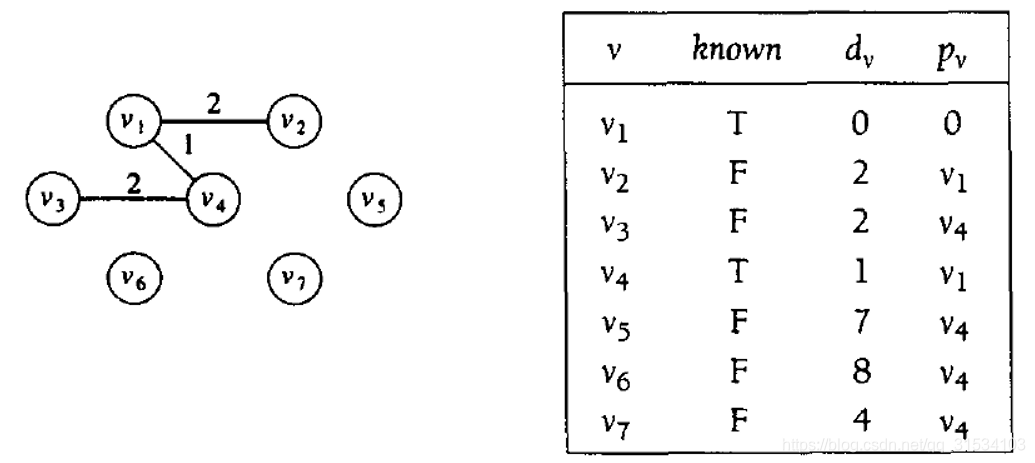
3. 重复：将 v2、3 加入到 T 中，更新邻接于 v2、3 的树外点到树 T 的距离。

   选择邻接边中权重最小的节点 v7 将其加入到 T 中。

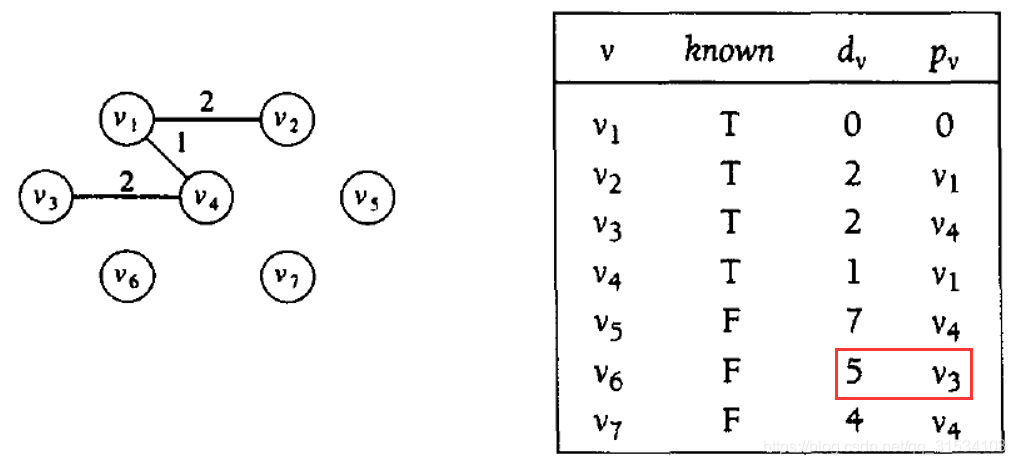
4. 重复：将 v7 加入到 T 中，更新邻接于 v7 的树外点到树 T 的距离。

   选择邻接边中权重最小的节点 v6 加入到 T 中。

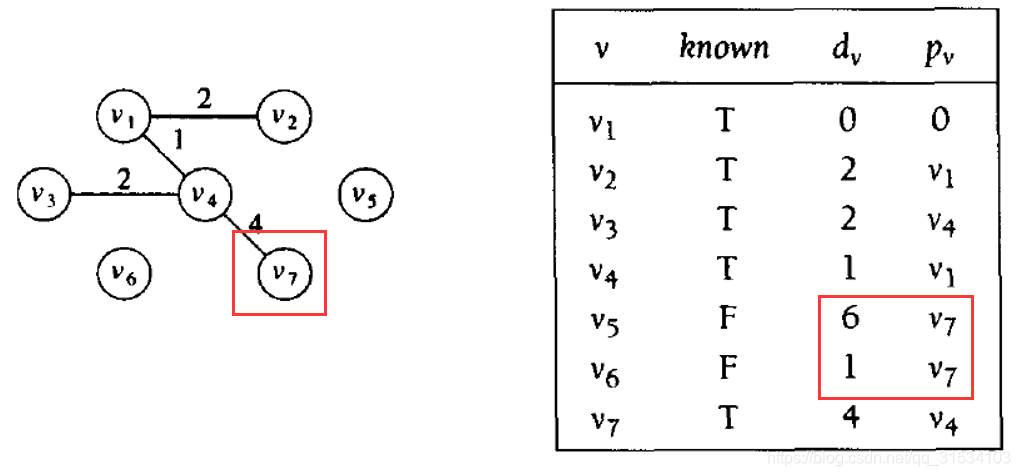
5. 重复 UNTIL：增加了n - 1條邊為止。(假設有 n 個節點)

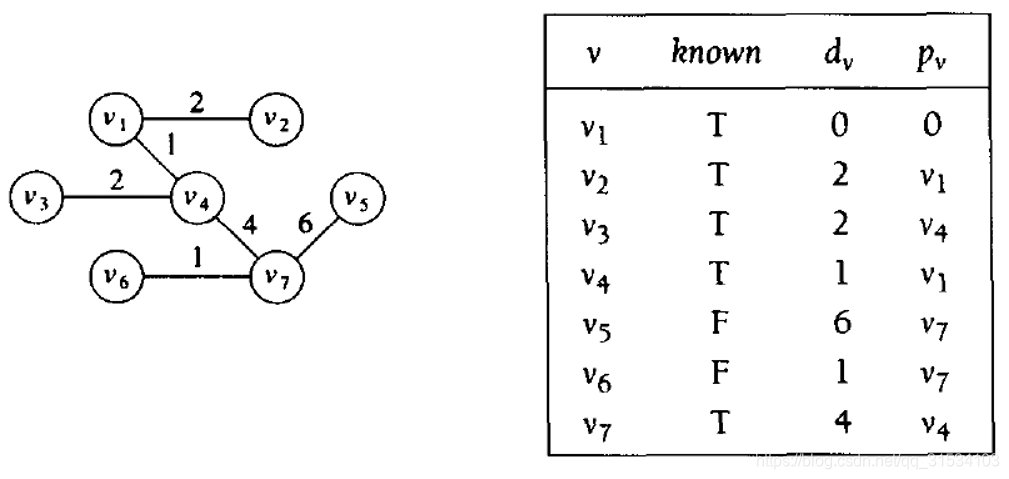
与 Dijkstra 的差异

唯一差异：如何更新 dv

假设 w 为已知点，v 为未知点

• Dijkstra: dv=min{dv, dw+c(w,v)} 其中 dv、w的含义是由源点到 v、w的路径和
• Prim: dv=min{dv, c(w,v)} 其中 dv、w的含义是到树中父节点的距离，如果 dv=c(w,v) 成立，则v的父节点修改为w

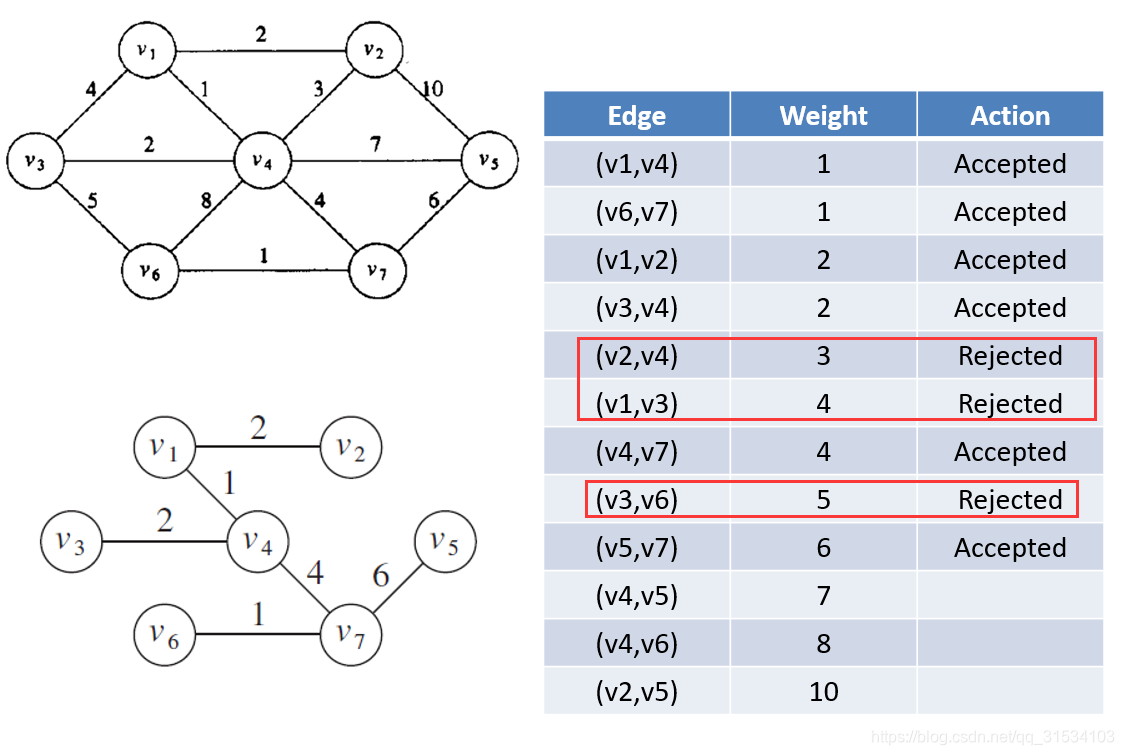
2.Kruskal’s algorithm（克鲁斯卡尔算法）

实现

先将边按 权重 从小到大排序，然后依次取边，注意如果加入该边会形成回路时，要reject掉。