1. 费马因式分解
1> 对于任一个奇数n,n = ab = x2-y2
2> ∵ n = ab = (x+y)*(x-y)
∴ a = x + y, b = x-y
x = (a+b)/2, y = (a-b)/2 (因为n为奇数,a, b必也为奇数,所以(a+b)和(a-b)必为偶数,故能被2整除,x, y为整数,x > y)
如:1 = 1*1 = 12 – 02
3 = 3*1 = 22 – 12
5 = 5*1 = 32 – 22
7 = 7*1 = 42 – 32
9 = 3*3 = 32 – 02
2. 费马因式分解算法
1> y2 = x2 – n
∵ x2 – n >= y2 >= 0
∴x2 >= n, x >= sqrt(n)
∴我们可以从x = sqrt(n)开始,计算x2 – n为完全平方数即可求出x, y,然后求得a, b
2> python代码
def Fermat(num): x = int(math.sqrt(num)); if x*x < num: x += 1; #y^2 = x^2 - num while(True): y2 = x*x - num; y = int(math.sqrt(y2)); if y*y == y2: break; x += 1; return [x+y, x-y];
3>. 利用完全平方数十位和个位数值性质改进费马因式分解算法
完全平方数的最后两个十进制数字(个位和十位)一定是下列数对之一:{00, e1, e4, 25, o6, e9}, 证明见《完全平方数的末两位数字类型的另一种证明》
#PerfectSquare = {00, e1, e4, 25, o6, e9} def CheckPerfectSquare(num): #tens = 3, mean it is a odd number, tens = 4, mean it is a even number, otherwise, tens equal the value digitList = [ {'unit' : 0, 'tens' : 0}, {'unit' : 1, 'tens' : 4}, {'unit' : 4, 'tens' : 4}, {'unit' : 5, 'tens' : 2}, {'unit' : 6, 'tens' : 3}, {'unit' : 9, 'tens' : 4}]; unit = num % 10; tens = (num % 100) / 10; for item in digitList: if item['unit'] == unit: if item['tens'] < 3: return item['tens'] == tens; else: #Check is odd or even number, check the first bit return item['tens'] & 1 == tens & 1; return False; def Fermat(num): x = int(math.sqrt(num)); if x*x < num: x += 1; times = 0; x0 = x; #y^2 = x^2 - num while(True): y2 = x*x - num; if CheckPerfectSquare(y2): times += 1; y = int(math.sqrt(y2)); if y*y == y2: break; x += 1; print "Loop : ", x - x0 +1, ", check perfect square :", times; print "x :", x, ", y :", y; return [x+y, x-y];
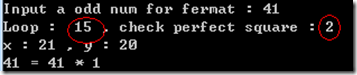
测试结果:
可以看出,用了完全平方数的性质后,将原来需要计算y的开方和比较y2的次数减少了13次(86%),我们知道计算乘法和开方式非常耗费时间的,减少这些次数后可以大大提高算法效率
4. 费马因式分解最坏计算次数
x = (a+b)/2
∵ n = ab, b = n/a
∴ x = (a + n/a)/2
我们需求x的最大值,如果(a + n/a)是单调递增或递减的,我们很容易就得到x的最大值
设a >= b(b >=a 也一样)
则 a2 >= ab = n
∴ a2 >= n (a <= n)
设f(a) = a + n/a
f(a+1) = (a+1) + n/(a+1)
f(a+1) – f(a) = (a+1) + n/(a+1) – (a + n/a)
= 1 + n/(a+1) – n/a
= [(a+1)a + na –n(a+1)]/a
= (a2 –n + a)/[a(a+1)]
∵ a2 >= n
∴ (a2 –n + a) > 0
∴f(a+1) > f(a)
∴f(a)时单调递增的
∵a <= n
∴当a = n时,f(a)最大,x也最大,x = (n + n/n)/2 = (n+1)/2
∴费马因式分解最大次数 = x – sqrt(n) = (n+1)/2 – sqrt(n)
5. 费马因式分解算法和素数判定
思考:当费马因式分解算法为最坏次数时,n是什么数
当费马因式分解算法为最坏次数时,可知a = n, b = 1, x = (n+1)/2, y = (n-1)/2
貌似其因子为本身和1,这和素数的性质非常像,看第1部分的1到9的费马因式分解,貌似满足这种条件的都是素数,那么大胆猜想一下:
假设:如果奇数n的费马因式分解式 = n*1, 那么n为一个素数
反证:n不为素数, 则x在最大值之前就使x2 – n = y2
即需证明,当n不为素数,n = ab = (x+y)(x-y), x < (n+1)/2
那么 n = ab (n > a)
根据第4部分证明知 x = (a + n/a)/2 ,且f(a) = a + n/a 是单调递增的
∵a < n
∴f(a) < f(n) < n + n/n = n + 1
∴x < (n+1)/2
∴x不可能到最大次数,得证
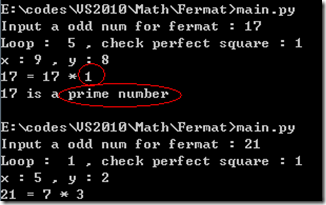
增加部分code和测试如下:
if __name__ == '__main__': while(True) : num = int(raw_input("Input a odd num for fermat : ")); if(1 == num & 1): break; retList = Fermat(num); print num, "=", retList[0], "*", retList[1]; if num > 1 and 1 == retList[1]: print num, "is a prime number";