Andrew Ng 机器学习笔记---by Orangestar
Week4_Neural Networks : Representation
1. Non-linear Hypotheses
当特征量非常多的时候,训练分类器is not a good idea
会产生非常多的特征量
而,神经网络则可以在特征量非常大的时候,works well
2. Neurons and the Brain
神经网络的最初目的是,模仿人脑
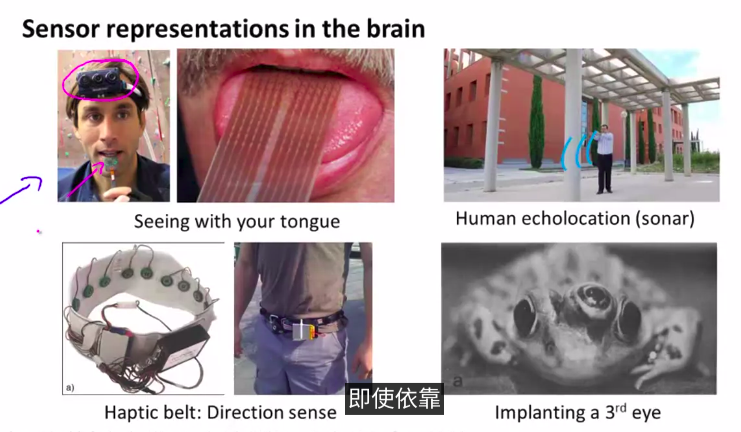
大脑的神奇之处
3. Model Representation I(一些术语)
如何表示神经网络?
人脑中的神经网络


至于电脑上面的神经模型,我们通过非常简单的构造来模拟神经元的工作
一个模型例子
树突,轴突
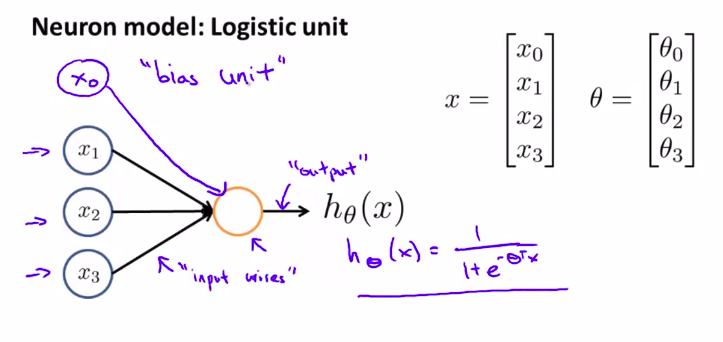
一些术语:
Sigmoid(logistic) activation function:激励函数
( heta)我们可能叫它叫做一个东西的权重,也叫参数
其中我们而外加的x_0,可以叫做偏执单元bias unit,
偏置单元一般都设为1,再通过需要进行调整
上面的只是一个十分简单的神经元模型
接下来看看更复杂的及其一些定义术语
从左到右,分别叫做:
输入层,隐藏层,输出层
输入层/输出层:顾名思义,输出或者输入参数
隐藏层:训练集中看不到的层
事实上,所有非输出层和输入层的,都叫隐藏层
那么,如何计算?
如下图 计算步骤

为什么是3*4?
因为,bias, heta_0,和x_0没有写出来!
所以,总结
如果网络有(s_j) 个单元在 j层上,(s_{j+1})在j+1上,
则( heta^{(j)}) 的维数就是(s_{j+1} * (s_j+1))
就是,( heta^{(j)})是射线,能设多少条线都不会计算吗!?
可以联想映射的内容
4. Model Representation II (展示一个向量化的实现方法)(前向传播)
在之前,计算可以表示为向量计算
Forward propagation: Vectorized implementation
前向传播!
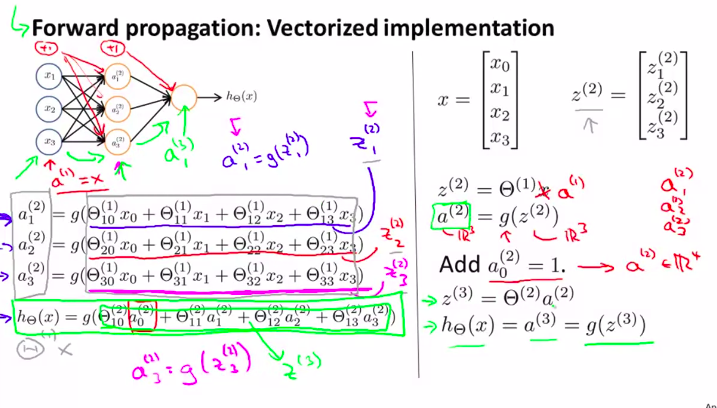
向量化实现方法
由线性代数知识不难理解!
就是把多项式方程组用矩阵或者向量来表示
-
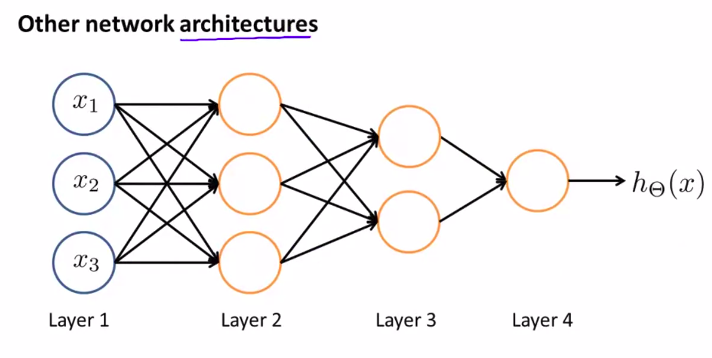
Other network architectures
architectures指的是神经元的架构
本节总结
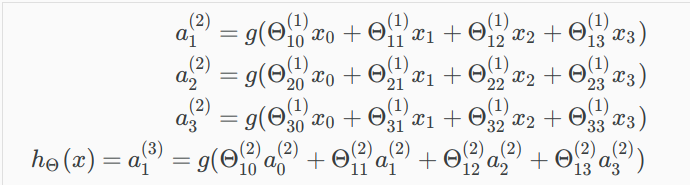
这是上节的计算神经元的方法
这节我们用向量来计算
定义了一个新的变量(z^{(j)}_k)
其中,J代表第几层。k代表第几个节点node就是说:(举个小栗子)

然后,
所以,用向量来表示就是:

其中,x就是第一层(输入层)的向量表示。只不过换了一个符号。(x = a^{(1)})
复写方程为:(z^{(j)} = Theta^{(j-1)}a^{(j-1)})
注释:
*我们可以将矩阵$Theta^{(j-1)} $ 乘与a(j-1),来得到z(j)
[$Theta{(j-1)} $]: 维数为×(n+1),其中s_j是激励节点的数量)
如图:
然后,可以得到a^(j)
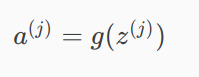
计算完之后,可以加上偏置项

然后:

5. 神经元的具体例子1
为什么神经网络可以用来学习复杂的非线性假设?
在下面这个例子中,x_1和x_2只有0,1两个取值。
所以,
y只有2个取值
OR或,AND与,XOR异或,NOR或非,NAND与非,XNOR异或非 异或只当两个数相同取0,不同取1
所以,图像为:

-
下面讲解其中的神经元(与)其他的大同小异
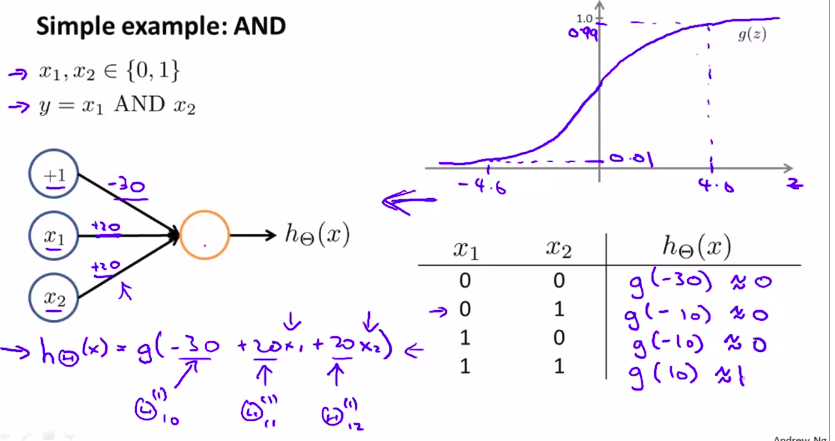
线上的数值为权重
右下角的表格叫做真值表
6.如何计算非线性的假设函数
先看一个NOT X_1的神经元
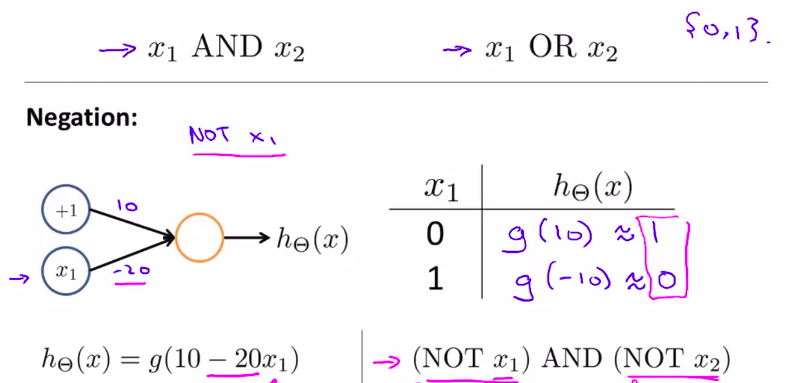
嘛...差不多就这种感觉,要建立逻辑电路差不多,就把加权附上去,按照你想让它怎么样
然后,我们可以将逻辑神经元进行组合:
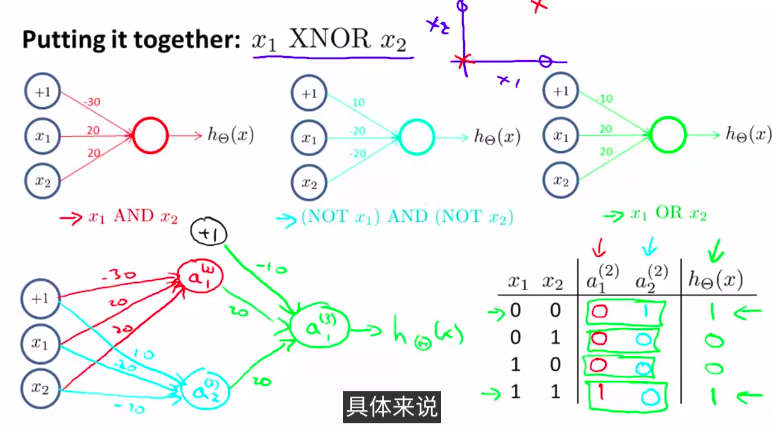
如图,组合为一个x_1 XNOR x_2
这样就可以计算出一个很复杂的函数
可以用矩阵来表示:
然后可以conbine起来。做出一个更复杂的逻辑门:
其中:
7. Multiclass Classification 用神经网络做多类别分类
直观感受,只要设多几个分类器就行
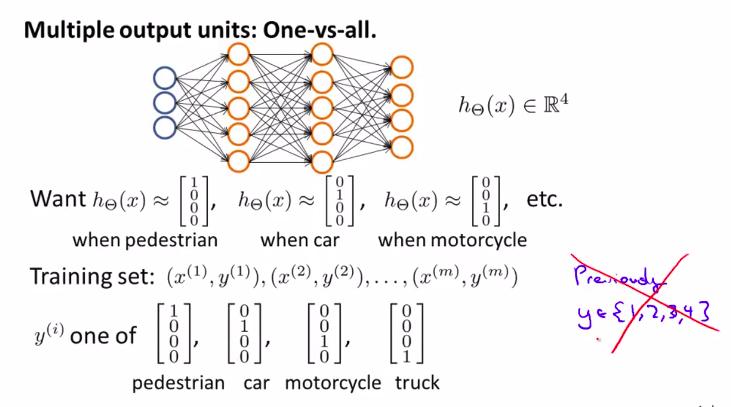
多分类的时候,一般y值为如图所示,而不是简单的数值,因为这样更容易表示!