

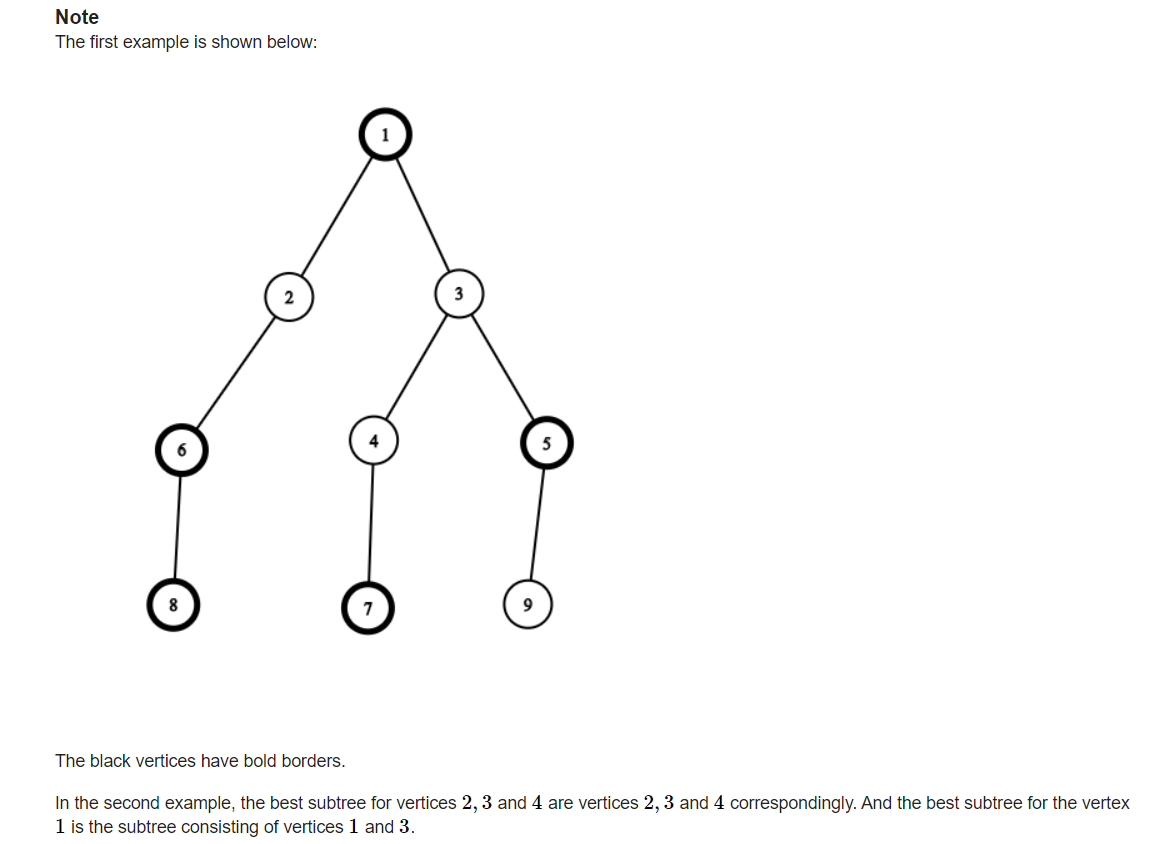
思路
令黑点点权为 -1 , 白点点权为 1,求最大子树点权和。
设 f[i] 为包含 i 点的最大子树点权值,如果当前点的最大点权和 比 当前点父亲的最大点权和小, 则更新当前点。
比较蠢的做法是,分两种情况讨论下,当前点的点权和 大于 或 小于 0 的情况处理是不同的。
如果当前点子树权值 >= 0,且父亲的子树权值更大,应该把父亲点的子树归并到当前点的子树中。
如果当前点子树权值 < 0,且父亲的子树中白的比黑的多,就把父亲点的子树归并到当前点子树上。
CODE
#include <bits/stdc++.h>
#define dbg(x) cout << #x << "=" << x << endl
#define eps 1e-8
#define pi acos(-1.0)
using namespace std;
typedef long long LL;
const int inf = 0x3f3f3f3f;
template<class T>inline void read(T &res)
{
char c;T flag=1;
while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;res=c-'0';
while((c=getchar())>='0'&&c<='9')res=res*10+c-'0';res*=flag;
}
namespace _buff {
const size_t BUFF = 1 << 19;
char ibuf[BUFF], *ib = ibuf, *ie = ibuf;
char getc() {
if (ib == ie) {
ib = ibuf;
ie = ibuf + fread(ibuf, 1, BUFF, stdin);
}
return ib == ie ? -1 : *ib++;
}
}
int qread() {
using namespace _buff;
int ret = 0;
bool pos = true;
char c = getc();
for (; (c < '0' || c > '9') && c != '-'; c = getc()) {
assert(~c);
}
if (c == '-') {
pos = false;
c = getc();
}
for (; c >= '0' && c <= '9'; c = getc()) {
ret = (ret << 3) + (ret << 1) + (c ^ 48);
}
return pos ? ret : -ret;
}
const int maxn = 2e5 + 7;
int a[maxn];
int n;
int head[maxn << 1], edge[maxn << 1], nxt[maxn << 1], cnt;
int f[maxn];
bool vis[maxn];
int ans[maxn];
void BuildGraph(int u, int v) {
cnt++;
edge[cnt] = v;
nxt[cnt] = head[u];
head[u] = cnt;
}
void dfs(int u, int fa) {
if(a[u] == 1) {
f[u] = 1;
}
else {
f[u] = -1;
}
//printf("f[%d]:%d
",u, f[u]);
for ( int i = head[u]; i; i = nxt[i] ) {
int v = edge[i];
if(v == fa)
continue;
else {
dfs(v, u);
if(f[v] > 0) {
f[u] += f[v];
//printf("f[%d]:%d
",u, f[u]);
}
}
}
}
void dp(int u, int fa) {
if(f[u] >= 0) {
int temp = f[fa] - f[u];
if(temp >= 0) {
f[u] += temp;
//printf("f[%d]:%d
",u, f[u]);
}
}
else {
//printf("fa: f[%d]:%d
",fa, f[fa]);
if(f[fa] >= 0) {
f[u] += f[fa];
//printf("f[%d]:%d
",u, f[u]);
}
}
for ( int i = head[u]; i; i = nxt[i] ) {
int v = edge[i];
//dbg(v);
if(v == fa)
continue;
else {
dp(v, u);
}
}
}
int main()
{
read(n);
for ( int i = 1; i <= n; ++i ) {
read(a[i]);
}
for ( int i = 1; i < n; ++i ) {
int u, v;
read(u);
read(v);
BuildGraph(u, v);
BuildGraph(v, u);
}
dfs(1, 1);
dp(1, 1);
for ( int i = 1; i <= n; ++i ) {
printf("%d ",f[i]);
}
return 0;
}