Use PSO to find minimum in OpenCASCADE

Use PSO to find minimum in OpenCASCADE

eryar@163.com

Abstract. Starting from OCCT6.8.0 will include one more algorithm for solving global optimization problems. Its development has been triggered by insufficient performance and robustness of existing algorithm of minimization of curve-surface distance in Extrema package. The PSO, Algorithms in this family are stochastic, and this feature can be perceived as opposite to robustness. However, we found it was not only much faster than original deterministic one, but also more robust in complex real-world situations. In particular, it has been able to find solution in situations like tangential or degenerated geometries where deterministic algorithms work poor and require extensive oversampling for robust results. The paper mainly focus on the usage and applications of the PSO algorithm.

Key Words. PSO, Particle Swarm Optimization, Minimization

1.Introduction

粒子群优化(Particle Swarm Optimization, PSO)算法是Kennedy和Eberhart受人工生命研究结果的启发、通过模拟鸟群觅食过程中的迁徙和群聚行为而提出的一种基于群体智能的全局随机搜索算法，自然界中各种生物体均具有一定的群体行为，而人工生命的主要研究领域之一是探索自然界生物的群体行为，从而在计算机上构建其群体模型。自然界中的鸟群和鱼群的群体行为一直是科学家的研究兴趣，生物学家Craig Reynolds在1987年提出了一个非常有影响的鸟群聚集模型，在他的仿真中，每一个个体遵循：

      (1) 避免与邻域个体相冲撞；

      (2) 匹配邻域个体的速度；

      (3) 飞向鸟群中心，且整个群体飞向目标。

仿真中仅利用上面三条简单的规则，就可以非常接近的模拟出鸟群飞行的现象。1995年，美国社会心理学家James Kennedy和电气工程师Russell Eberhart共同提出了粒子群算法，其基本思想是受对鸟类群体行为进行建模与仿真的研究结果的启发。他们的模型和仿真算法主要对Frank Heppner的模型进行了修正，以使粒子飞向解空间并在最好解处降落。Kennedy在他的书中描述了粒子群算法思想的起源。

粒子群优化由于其算法简单，易于实现，无需梯度信息，参数少等特点在连续优化问题和离散问题中都表现出良好的效果，特别是因为其天然的实数编码特点适合处理实优化问题。近年来成为国际上智能优化领域研究的热点。PSO算法最早应用于非线性连续函数的优化和神经元网络的训练，后来也被用于解决约束优化问题、多目标优化问题，动态优化问题等。

在OpenCASCADE中很多问题可以归结为非线性连续函数的优化问题，如求极值的包中计算曲线和曲面之间的极值点，或曲线与曲线间的极值点等问题。本文主要关注OpenCASCADE中PSO的用法，在理解其用法的基础上再来理解其他相关的应用。

2. PSO Usage

为了提高程序的性能及稳定性，OpenCASCADE引入了智能化的算法PSO（Particle Swarm Optimization），相关的类为math_PSO，其类声明的代码如下：

//! In this class implemented variation of Particle Swarm Optimization (PSO) method.
//! A. Ismael F. Vaz, L. N. Vicente 
//! "A particle swarm pattern search method for bound constrained global optimization"
//!
//! Algorithm description:
//! Init Section:
//! At start of computation a number of "particles" are placed in the search space.
//! Each particle is assigned a random velocity.
//!
//! Computational loop:
//! The particles are moved in cycle, simulating some "social" behavior, so that new position of
//! a particle on each step depends not only on its velocity and previous path, but also on the
//! position of the best particle in the pool and best obtained position for current particle.
//! The velocity of the particles is decreased on each step, so that convergence is guaranteed.
//!
//! Algorithm output:
//! Best point in param space (position of the best particle) and value of objective function.
//!
//! Pros:
//! One of the fastest algorithms.
//! Work over functions with a lot local extremums.
//! Does not require calculation of derivatives of the functional.
//!
//! Cons:
//! Convergence to global minimum not proved, which is a typical drawback for all stochastic algorithms.
//! The result depends on random number generator.
//!
//! Warning: PSO is effective to walk into optimum surrounding, not to get strict optimum.
//! Run local optimization from pso output point.
//! Warning: In PSO used fixed seed in RNG, so results are reproducible.

class math_PSO
{
public:

  /**
  * Constructor.
  *
  * @param theFunc defines the objective function. It should exist during all lifetime of class instance.
  * @param theLowBorder defines lower border of search space.
  * @param theUppBorder defines upper border of search space.
  * @param theSteps defines steps of regular grid, used for particle generation.
                    This parameter used to define stop condition (TerminalVelocity).
  * @param theNbParticles defines number of particles.
  * @param theNbIter defines maximum number of iterations.
  */
  Standard_EXPORT math_PSO(math_MultipleVarFunction* theFunc,
                           const math_Vector& theLowBorder,
                           const math_Vector& theUppBorder,
                           const math_Vector& theSteps,
                           const Standard_Integer theNbParticles = 32,
                           const Standard_Integer theNbIter = 100);

  //! Perform computations, particles array is constructed inside of this function.
  Standard_EXPORT void Perform(const math_Vector& theSteps,
                               Standard_Real& theValue,
                               math_Vector& theOutPnt,
                               const Standard_Integer theNbIter = 100);

  //! Perform computations with given particles array.
  Standard_EXPORT void Perform(math_PSOParticlesPool& theParticles,
                               Standard_Integer theNbParticles,
                               Standard_Real& theValue,
                               math_Vector& theOutPnt,
                               const Standard_Integer theNbIter = 100);

private:

  void performPSOWithGivenParticles(math_PSOParticlesPool& theParticles,
                                    Standard_Integer theNbParticles,
                                    Standard_Real& theValue,
                                    math_Vector& theOutPnt,
                                    const Standard_Integer theNbIter = 100);

  math_MultipleVarFunction *myFunc;
  math_Vector myLowBorder; // Lower border.
  math_Vector myUppBorder; // Upper border.
  math_Vector mySteps; // steps used in PSO algorithm.
  Standard_Integer myN; // Dimension count.
  Standard_Integer myNbParticles; // Particles number.
  Standard_Integer myNbIter;
};

math_PSO的输入主要为：求极小值的多元函数math_MultipleVarFunction，各个自变量的取值范围。下面通过一个具体的例子来说明如何将数学问题转换成代码，利用程序来求解。在《最优化方法》中找到如下例题：

实现代码如下所示：

/*
Copyright(C) 2017 Shing Liu(eryar@163.com)

Permission is hereby granted, free of charge, to any person obtaining a copy
of this software and associated documentation files(the "Software"), to deal
in the Software without restriction, including without limitation the rights
to use, copy, modify, merge, publish, distribute, sublicense, and / or sell
copies of the Software, and to permit persons to whom the Software is
furnished to do so, subject to the following conditions :

The above copyright notice and this permission notice shall be included in all
copies or substantial portions of the Software.

THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT.IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
SOFTWARE.
*/

// NOTE
// ----
// Tool: Visual Studio 2013 & OpenCASCADE7.1.0
// Date: 2017-04-18  20:52 

#include <math_PSO.hxx>

#pragma comment(lib, "TKernel.lib")
#pragma comment(lib, "TKMath.lib")

// define function:
// f(x) = x1 - x2 + 2x1^2 + 2x1x2 + x2^2
class TestFunction : public math_MultipleVarFunction
{
public:
    virtual Standard_Integer NbVariables() const
    {
        return 2;
    }

    virtual Standard_Boolean Value(const math_Vector& X, Standard_Real& F)
    {
        F = X(1) - X(2) + 2.0 * X(1) * X(1) + 2.0 * X(1) * X(2) + X(2) * X(2);

        return Standard_True;
    }

};


void test()
{
    TestFunction aFunction;
    math_Vector aLowerBorder(1, aFunction.NbVariables());
    math_Vector aUpperBorder(1, aFunction.NbVariables());
    math_Vector aSteps(1, aFunction.NbVariables());

    aLowerBorder(1) = -10.0;
    aLowerBorder(2) = -10.0;

    aUpperBorder(1) = 10.0;
    aUpperBorder(2) = 10.0;

    aSteps(1) = 0.1;
    aSteps(2) = 0.1;

    Standard_Real aValue = 0.0;
    math_Vector aOutput(1, aFunction.NbVariables());

    math_PSO aPso(&aFunction, aLowerBorder, aUpperBorder, aSteps);
    aPso.Perform(aSteps, aValue, aOutput);

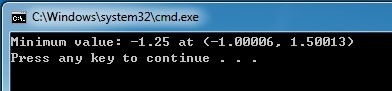
    std::cout << "Minimum value: " << aValue << " at (" << aOutput(1) << ", " << aOutput(2) << ")" << std::endl;

}

int main(int argc, char* argv[])
{
    test();

    return 0;
}

计算结果为最小值-1.25, 在x1=-1，x2=1.50013处取得，如下图所示：

3.Applications

计算曲线和曲面之间的极值，也是一个计算多元函数的极值问题。对应的类为Extrema_GenExtCS。

4.Conclusion

常见的优化算法如共轭梯度法、Netwon-Raphson法（math_NewtonMinimum），Fletcher-Reeves法（math_FRPR）、Broyden-Fletcher-Glodfarb-Shanno法（math_BFGS）等都是局部优化方法，所有这些局部优化方法都是针对无约束优化问题提出的，而且对目标函数均有一定的解析性要求，如Newton-Raphson要求目标函数连续可微，同时要求其一阶导数连续。OpenCASCADE中的math_NewtonMinimu中还要求多元函数具有Hessian矩阵，即二阶导数连续。

随着现科学技术的不断发展和多学科的相互交叉与渗透，很多实际工程优化问题不仅需要大量的复杂科学计算，而且对算法的实时性要求也特别高，这些复杂优化问题通常具有以下特点：

1) 优化问题的对象涉及很多因素，导致优化问题的目标函数的自变量维数很多，通常达到数百维甚至上万维，使得求解问题的计算量大大增加；

2) 优化问题本身的复杂性导致目标函数是非线性，同时由于有些目标函数具有不可导，不连续、极端情况下甚至函数本身不能解析的表达；如曲线或曲面退化导致的尖点或退化点的不连续情况；

3) 目标函数在定义域内具有多个甚至无数个极值点，函数的解空间形状复杂。

当以上三个因素中一个或几个出现在优化问题中时，将会极大地增加优化问题求解的困难程度，单纯地基于解析确定性的优化方法很难奏效，因此必须结合其他方法来解决这些问题。

PSO算法简单，易于实现且不需要目标函数的梯度（一阶可导）和Hassian矩阵（二阶可导），速度快，性能高。但是PSO也有不足之处，这是许多智能算法的共性，即只能找到满足条件的解，这个解不能确定为精确解。

5.References

1. aml. Application of stohastic algorithms in extrema. https://dev.opencascade.org/index.php?q=node/988

2. 何坚勇. 最优化方法. 清华大学出版社. 2007

3. 沈显君. 自适应粒子群优化算法及其应用. 清华大学出版社. 2015

4. 汪定伟, 王俊伟, 王洪峰, 张瑞友, 郭哲. 智能优化方法. 高等教育出版社. 2007

PDF Version: Use PSO to find minimum in OpenCASCADE