题目

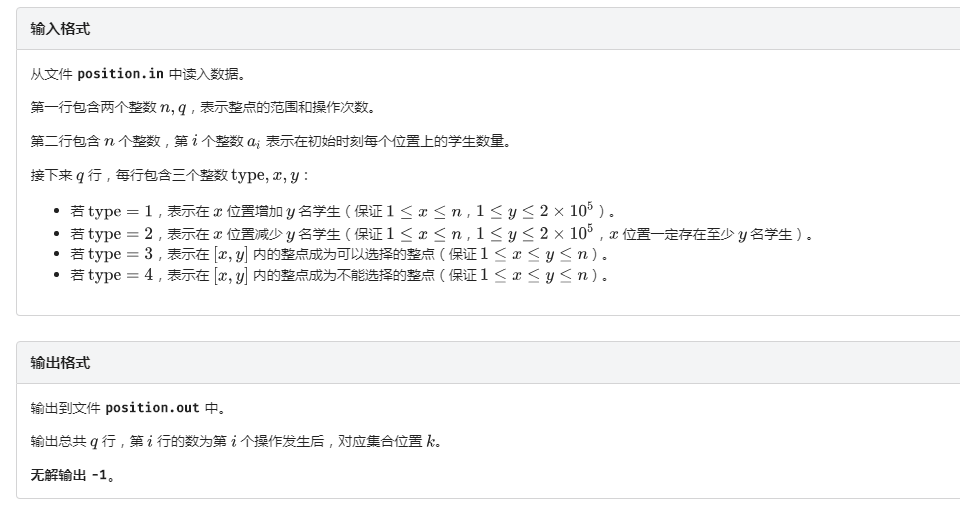

题解
部分分的做法这里就不说了 相信聪明的你一定会的
考试的时候肯定是不会做了 之前翻了一些题解慢慢理解
前置芝士
线段树(树状数组)、带权中位数
如果题目没有限制不能取的位置 那么答案就是带权中位数,带权中位数的定义详细参考百科:
https://baike.baidu.com/item/带权中位数/8517609#2
我们要取第一个满足前缀和>=[(sum+1)/2] 可以用线段树或者树状数组查询
int query(int id, int l, int r, long long k) { if (l == r) return l; int mid = l + r >> 1; if (t[id << 1].s >= k) return query(id << 1, l, mid, k); else return query(id << 1 | 1, mid + 1, r, k - t[id << 1].s); }
本题加上了限制 某些位置不能取
那么假设第一个满足前缀和>=[(sum+1)/2]的位置为mid 则答案就是在[1,mid]中取能取到的最右端,[mid,n]中取能取到的最左端 再比较两者的值取最小
具体的 我们可以用线段树维护一个区间可以取到的最左端和最右端以及整个区间移到区间左端点的值和移到区间右端点的值
对于查询 就是查询[1,mid]中能取到的最右端以及[mid,n]中取能取到的最左端 再比较两者的值的最小值就是最后答案 如果两者都不存在 则输出-1
贴代码
#include <bits/stdc++.h> using namespace std; const int N = 2e5 + 5; const long long INF = 1e17; struct T { int lb, rb, tag, sb; long long sl, sr, s; // lb 左边能选的最远地方 // rb 右边能选的最远地方 // tag 懒标记 0代表能取 1代表不能取 // sb 能选的区间长度 // sl 全部移到左端点的值 // sr 全部移到右端点的值 } t[N << 2]; int n, m; struct A { int x; //位置 long long y; //所有移动到x的总代价 }; int a[N]; void pushup(int id, int l, int r) { int mid = l + r >> 1; t[id].lb = t[id << 1].lb ? t[id << 1].lb : t[id << 1 | 1].lb; t[id].rb = t[id << 1 | 1].rb ? t[id << 1 | 1].rb : t[id << 1].rb; t[id].sb = t[id << 1].sb + t[id << 1 | 1].sb; t[id].s = t[id << 1].s + t[id << 1 | 1].s; t[id].sl = t[id << 1].sl + t[id << 1 | 1].sl + t[id << 1 | 1].s * (mid - l + 1); t[id].sr = t[id << 1 | 1].sr + t[id << 1].sr + t[id << 1].s * (r - mid); } void pushdown(int id, int l, int r) { if (t[id].tag == -1) return; int mid = l + r >> 1; if (!t[id].tag) { t[id << 1].tag = t[id << 1 | 1].tag = t[id].tag; t[id << 1].lb = l; t[id << 1].rb = mid; t[id << 1].sb = mid - l + 1; t[id << 1 | 1].lb = mid + 1; t[id << 1 | 1].rb = r; t[id << 1 | 1].sb = r - mid; } else { t[id << 1].tag = t[id << 1 | 1].tag = t[id].tag; t[id << 1].lb = t[id << 1].rb = t[id << 1].sb = 0; t[id << 1 | 1].lb = t[id << 1 | 1].rb = t[id << 1 | 1].sb = 0; } t[id].tag = -1; } void add(int id, int l, int r, int pos, long long y) { if (l == r) { t[id].s += y; return; } pushdown(id, l, r); int mid = l + r >> 1; if (pos <= mid) add(id << 1, l, mid, pos, y); else add(id << 1 | 1, mid + 1, r, pos, y); pushup(id, l, r); } void build(int id, int l, int r) { if (l == r) { t[id].s = a[l]; t[id].rb = t[id].lb = l; t[id].sb = 1, t[id].tag = -1; return; } int mid = l + r >> 1; build(id << 1, l, mid); build(id << 1 | 1, mid + 1, r); pushup(id, l, r); } void modify(int id, int l, int r, int x, int y, bool b) { if (x <= l && r <= y) { t[id].tag = b; if (!b) t[id].lb = l, t[id].rb = r, t[id].sb = r - l + 1; else t[id].lb = t[id].rb = t[id].sb = 0; return; } pushdown(id, l, r); int mid = l + r >> 1; if (x <= mid) modify(id << 1, l, mid, x, y, b); if (y > mid) modify(id << 1 | 1, mid + 1, r, x, y, b); pushup(id, l, r); } int query(int id, int l, int r, long long k) { if (l == r) return l; int mid = l + r >> 1; if (t[id << 1].s >= k) return query(id << 1, l, mid, k); else return query(id << 1 | 1, mid + 1, r, k - t[id << 1].s); } A get_R(int id, int l, int r, int x, int y) { A ans; if (!t[id].sb || x > y) return ans = A{ 0, INF }; if (l == r) return ans = A{ l, 0 }; pushdown(id, l, r); int mid = l + r >> 1; if (t[id << 1 | 1].lb && t[id << 1 | 1].lb <= y) { //要查询最右端 所以先在右半段找 A ans = get_R(id << 1 | 1, mid + 1, r, max(x, mid + 1), y); if (ans.x) ans.y += t[id << 1].sr + t[id << 1].s * (ans.x - mid); return ans; } else { //不在右半段则往左半段找 A ans = get_R(id << 1, l, mid, x, min(mid, y)); if (ans.x) ans.y += t[id << 1 | 1].sl + t[id << 1 | 1].s * (mid - ans.x + 1); return ans; } } A get_L(int id, int l, int r, int x, int y) { A ans; if (!t[id].sb || x > y) return ans = A{ 0, INF }; if (l == r) return ans = A{ l, 0 }; pushdown(id, l, r); int mid = l + r >> 1; if (t[id << 1].rb && t[id << 1].rb >= x) { //要查询最左端 所以先在左半段找 A ans = get_L(id << 1, l, mid, x, min(mid, y)); if (ans.x) ans.y += t[id << 1 | 1].sl + t[id << 1 | 1].s * (mid - ans.x + 1); return ans; } else { //不在左半段则往右半段找 A ans = get_L(id << 1 | 1, mid + 1, r, max(x, mid + 1), y); if (ans.x) ans.y += t[id << 1].sr + t[id << 1].s * (ans.x - mid); return ans; } } int main() { freopen("position.in", "r", stdin); freopen("position.out", "w", stdout); cin >> n >> m; long long sum = 0; for (int i = 1; i <= n; ++i) scanf("%d", a + i), sum += a[i]; build(1, 1, n); while (m--) { int opt, x, y; scanf("%d%d%d", &opt, &x, &y); if (opt == 1) add(1, 1, n, x, y), sum += y; if (opt == 2) add(1, 1, n, x, -y), sum -= y; if (opt == 3) modify(1, 1, n, x, y, 0); if (opt == 4) modify(1, 1, n, x, y, 1); int mid = query(1, 1, n, (sum + 1) >> 1); A l = get_R(1, 1, n, 1, mid); A r = get_L(1, 1, n, mid, n); if (!l.x && !r.x) printf("-1 "); else printf("%d ", l.y <= r.y ? l.x : r.x); } }
也有树状数组的做法 博主觉得线段树比较容易理解 其他做法留给聪明的读者自行学习