Problem Codeforces #548 (Div2) - D.Steps to One
Time Limit: 2000 mSec
![]() Problem Description
Problem Description

Input
The first and only line contains a single integer mm (1≤m≤100000,1≤m≤100000).
![]() Output
Output
Print a single integer — the expected length of the array aa written as P⋅Q^−1(mod10^9+7)
![]() Sample Input
Sample Input
4
![]() Sample Output
Sample Output
333333338
题解:概率dp做的太少了,不会做。。。
首先是状态定义,dp[x]表示当前序列的gcd为x的情况下,还能添加数字个数的期望值,看了题解之后感觉这样很自然,但是自己想就想不到,有了这个定义之后状态转移就比较简单了,枚举下一个数字,根据期望的线性性质,有:
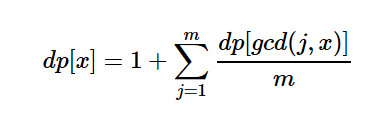
这样一来得到了一个O(n^2)的算法,显然不行,不过到这里的转化就很套路了,枚举gcd,式子化为:
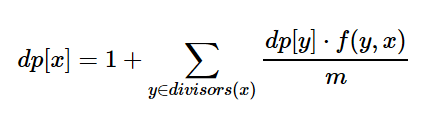
f(y, x)指的是和x的gcd是y的数有多少个(从1到m),预处理出1~m的约数,复杂度mlogm,这样不用根号m枚举约数,枚举y这一步题解中给出的均摊复杂度是logm,(不会证qwq,不过很多地方都是这么分析的),这样一来就只剩下f的求解了,设x = y * a,则和x的gcd为b的数必定可表达为 p = y * b且gcd(a, b) = 1,这样一来就相当于计算从1到m/y中和a互质的数的个数,也就是和a没有相同的质因子,打打表(看题解)可以发现在题目的范围内b的质因子数至多为6,容斥一下即可计数,最终复杂度O(mlogm*2^6*6),是可以接受的。代码是看了题解的代码之后写的,主要学习这里质因数分解的操作。
1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 #define REP(i, n) for (int i = 1; i <= (n); i++) 6 #define sqr(x) ((x) * (x)) 7 8 const int maxn = 100000 + 100; 9 const int maxm = 200000 + 100; 10 const int maxs = 10000 + 10; 11 12 typedef long long LL; 13 typedef pair<int, int> pii; 14 typedef pair<double, double> pdd; 15 16 const LL unit = 1LL; 17 const int INF = 0x3f3f3f3f; 18 const LL mod = 1000000007; 19 const double eps = 1e-14; 20 const double inf = 1e15; 21 const double pi = acos(-1.0); 22 23 LL pow_mod(LL x, LL n, LL mod) 24 { 25 LL base = x % mod; 26 LL ans = 1; 27 while (n) 28 { 29 if (n & 1) 30 { 31 ans = ans * base % mod; 32 } 33 base = base * base % mod; 34 n >>= 1; 35 } 36 return ans % mod; 37 } 38 39 LL m, invm; 40 unordered_map<int, int> prime[maxn]; 41 vector<LL> fact[maxn]; 42 bool is_prime[maxn]; 43 LL dp[maxn]; 44 45 void premanagement() 46 { 47 memset(is_prime, true, sizeof(is_prime)); 48 is_prime[0] = is_prime[1] = false; 49 for (LL i = 2; i < maxn; i++) 50 { 51 if (is_prime[i]) 52 { 53 for (LL j = i; j < maxn; j += i) 54 { 55 LL cnt = 0; 56 LL tmp = j; 57 while (tmp % i == 0) 58 { 59 cnt++; 60 tmp /= i; 61 } 62 prime[j][i] = cnt; 63 is_prime[j] = false; 64 } 65 is_prime[i] = true; 66 } 67 } 68 69 for (LL i = 1; i < maxn; i++) 70 { 71 for (LL j = 2 * i; j < maxn; j += i) 72 { 73 fact[j].push_back(i); 74 } 75 } 76 } 77 78 LL cal(LL x, LL n) 79 { 80 vector<LL> a; 81 LL curcnt = m / x; 82 for (auto &item : prime[n]) 83 { 84 if (!prime[x].count(item.first)) 85 { 86 a.push_back(item.first); 87 continue; 88 } 89 if (prime[x][item.first] == item.second) 90 { 91 continue; 92 } 93 else 94 { 95 a.push_back(item.first); 96 } 97 } 98 99 LL sz = a.size(); 100 LL lim = m / x; 101 for (LL sit = 1; sit < (unit << sz); sit++) 102 { 103 LL tag = 1; 104 LL val = 1; 105 for (LL j = 0; j < sz; j++) 106 { 107 if (sit & (unit << j)) 108 { 109 val *= a[j]; 110 tag *= -1; 111 } 112 } 113 curcnt += tag * (lim / val); 114 } 115 return curcnt; 116 } 117 118 int main() 119 { 120 ios::sync_with_stdio(false); 121 cin.tie(0); 122 //freopen("input.txt", "r", stdin); 123 //freopen("output.txt", "w", stdout); 124 cin >> m; 125 invm = pow_mod(m, mod - 2, mod); 126 premanagement(); 127 dp[1] = 0; 128 for (LL i = 2; i <= m; i++) 129 { 130 LL &ans = dp[i]; 131 ans = 1; 132 for (LL item : fact[i]) 133 { 134 ans += cal(item, i) * dp[item] % mod * invm % mod; 135 ans %= mod; 136 } 137 LL cnt = m / i; 138 ans = ans * m % mod * pow_mod(m - cnt, mod - 2, mod) % mod; 139 } 140 LL ans = 1; 141 for (LL i = 1; i <= m; i++) 142 { 143 ans = (ans + dp[i] * invm) % mod; 144 } 145 cout << ans << endl; 146 return 0; 147 }