高级数据结构---二叉查找树及其增删改查实现

二叉树查找树：

二叉查找树也叫二叉搜索树，二叉排序树。它也是一种特殊的二叉树，

它具有以下特点

1.如果它的左子树不为空，则左子树上结点的值都小于根结点。

2.如果它的右子树不为空，则右子树上结点的值都大于根结点。

3.子树的子树同样也要遵循以上两点

 

为什么又叫做二叉排序树，因为具有这种特殊特点的二叉树，它的中序遍历一定是有序的，如下：

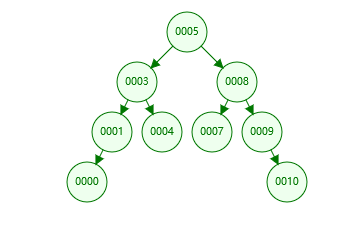
中序遍历的结果是0,1,3,4,5,7,8,9,10

推荐一个网站：https://www.cs.usfca.edu/~galles/visualization/Algorithms.html 这个上面有各种数据结构的操作，之前在mysql索引数据结构这篇文章中也推荐过。

插入的时候每次都是和根结点或者子树的根结点比较，大于走右边，小于走左边，直到找到它应该插入的位置。新元素插入的位置肯定值在叶子结点。其实它的插入就是一次查找。每次判断之后就会折半，所以说它的查询效率是O(logn)。

查询和插入的时候类似，修改就没什么好说的了，直接把数据覆盖上去即可

重点说下二叉查找树的删除。

它的删除分三种情况：

1.删除的是叶子结点数据，可以看出来，直接删除就可以了，比如上面0,4,7,10，将其双亲的对应子树指向null即可

2.删除的是度为1的结点，比如上面的1,9，只需要将它的子树的根结点覆盖当前删除的这个节点即可，以1的删除为例，也就是把其双亲3的右子树指针改指向像它的孩子0即可。

3.删除的结点度为2，也就有两棵子树的结点。这个的处理就稍微复杂一点了，因为二叉查找树的特性，根大于左子树小于右子树的。所以删除的需要去寻找前驱/后继结点来补充它的位置。如果删除的根左边的结点（比根小的结点），那么就是找前驱结点，前驱结点是其左子树中最大的结点，前驱结点的右子树一定为空，因为没有比它大的了；如果删除的根右边的结点（比根大的结点），那么就是找后继结点，后继结点是其右子树中最小的结点，后继结点的左子树一定为空，因为没有比它小的了。其实前驱后继就是中序遍历的时候在根前后的两个结点。如此一来，可以看出找到的前驱/后继结点的条件肯定是满足1或者2的，找到这个节点之后，将其覆盖当前要删除的这个节点。各项指针都移动好了，只需要将这个前驱/后继结点删除就可以了，这个节点的删除就和前面两种情况一样的了。

具体每一个注意点可以看下代码注释说明，应该算比较详细，里面涉及的那些结点指针的指向变更，还是比较绕的。

 

package com.nijunyang.algorithm.tree;

import com.nijunyang.algorithm.util.RefObject;

/**
 * Description:
 * Created by nijunyang on 2020/4/19 20:03
 */
public class BinarySearchTree<T extends Comparable<T>> extends TreeNode<T> {
    private T data;
    private BinarySearchTree<T> leftChild;
    private BinarySearchTree<T> rightChild;

    public BinarySearchTree(T data) {
        this.data = data;
    }

    public static void main(String[] args) {
        BinarySearchTree<Integer> binarySearchTree = new BinarySearchTree(5);
        BinarySearchTree.insert(binarySearchTree, 3);
        BinarySearchTree.insert(binarySearchTree, 1);
        BinarySearchTree.insert(binarySearchTree, 4);
        BinarySearchTree.insert(binarySearchTree, 8);
        BinarySearchTree.insert(binarySearchTree, 7);
        BinarySearchTree.insert(binarySearchTree, 9);
        BinarySearchTree.insert(binarySearchTree, 10);
        BinarySearchTree.insert(binarySearchTree, 0);
        TreeUtil.inOrderTraversal(binarySearchTree);
        System.out.println();
        TreeUtil.levelOrder(binarySearchTree);
        System.out.println();
        BinarySearchTree<Integer> integerBinarySearchTree = BinarySearchTree.find(binarySearchTree, 9, new RefObject<>());
        delete(binarySearchTree, 8);
        delete(binarySearchTree, 7);
        TreeUtil.inOrderTraversal(binarySearchTree);
    }

    /**
     * 插入数据
     * @param root
     * @param data
     * @param <T>
     */
    public static <T extends Comparable<T>> void insert(BinarySearchTree<T> root, T data) {
        if (root.data.compareTo(data) < 0) {
            if (root.rightChild == null) {
                root.rightChild = new BinarySearchTree(data);
            } else {
                insert(root.rightChild, data);
            }
        } else {
            if (root.leftChild == null) {
                root.leftChild = new BinarySearchTree(data);
            } else {
                insert(root.leftChild, data);
            }
        }
    }


    /**
     * 查询数据
     * @param root
     * @param data
     * @param parent   用于带出父节点
     * @param <T>
     * @return
     */
    public static <T extends Comparable<T>> BinarySearchTree<T> find(
            BinarySearchTree<T> root, T data, RefObject<BinarySearchTree<T>> parent) {
        if (root.data.compareTo(data) == 0) {
            return root;
        }
        parent.setValue(root);
        if (root.data.compareTo(data) < 0) {
            if (root.rightChild != null) {
                return find(root.rightChild, data, parent);
            }
        } else {
            if (root.leftChild != null) {
                return find(root.leftChild, data, parent);
            }
        }
        return null;
    }

    /**
     * 查询最大数据
     * @param root
     * @param parentRef  返回结果的父结点包装
     * @param <T>
     * @return
     */
    public static <T extends Comparable<T>> BinarySearchTree<T> findMax(
            BinarySearchTree<T> root, RefObject<BinarySearchTree<T>> parentRef) {
        if (root.rightChild != null) {
            parentRef.setValue(root);
            return findMax(root.rightChild, parentRef);
        }
        return root;
    }

    /**
     * 查询最小数据
     * @param root
     * @param parentRef 返回结果的父结点包装
     * @param <T>
     * @return
     */
    public static <T extends Comparable<T>> BinarySearchTree<T> findMin(
            BinarySearchTree<T> root, RefObject<BinarySearchTree<T>> parentRef) {
        if (root.leftChild != null) {
            parentRef.setValue(root);
            return findMin(root.leftChild, parentRef);
        }
        return root;
    }

    /**
     * 删除数据
     * @param root
     * @param data
     * @param <T>
     * @return
     */
    public static <T extends Comparable<T>> void delete(BinarySearchTree<T> root, T data) {

        RefObject<BinarySearchTree<T>> parentRef = new RefObject<>();
        BinarySearchTree<T> delBinarySearchTree = find(root, data, parentRef);
        if (delBinarySearchTree == null) {
            return;
        }
        /**
         * 二叉搜索树结点的删除分三种情况：
         * 1.叶子结点，可以直接删除
         * 2.度为1的结点，可以直接删除（只有一个子树的结点）
         * 3.两棵子树的结点删除，找前驱结点/后继结点。就是删除了该结点，前驱/后继结点可以直接补位
         * 如果删除的根左边的结点，那么就是找前驱结点，前驱结点是其左子树中最大的结点，前驱结点的右子树一定为空，因为没有比它大的了
         * 如果删除的根右边的结点，那么就是找后继结点，后继结点是其右子树中最小的结点，后继结点的左子树一定为空，因为没有比它小的了
         * 如此一来，可以看出找到的前驱/后继结点的条件肯定是满足1或者2的
         */
        BinarySearchTree<T> parent = parentRef.getValue();
        //叶子结点直接将父结点的孩子置空
        if (delBinarySearchTree.leftChild == null && delBinarySearchTree.rightChild == null) {
            if (parent.rightChild == delBinarySearchTree) {
                parent.rightChild = null;
            } else {
                parent.leftChild = null;
            }
        }
        //度为2的结点删除
        else if (delBinarySearchTree.leftChild != null && delBinarySearchTree.rightChild != null) {
            //删除比根大的，删除的结点在根的右边，需要找后继结点
            if (root.data.compareTo(data) < 0) {
                RefObject<BinarySearchTree<T>> postParentRef = new RefObject<>(); //后继结点的父结点
                BinarySearchTree<T> postNode = findMin(root.rightChild, postParentRef);
                //判断要删除的结点是它父结点的左结点还是右结点，修改对应指针指向后继结点
                if (parent.data.compareTo(delBinarySearchTree.data) < 0) {
                    parent.rightChild = postNode;
                } else {
                    parent.leftChild = postNode;
                }
                postParentRef.getValue().leftChild = null; //后继结点因为要移走，所以置空其父结点的左孩子（后继必定是其父的左孩子）
                if (postNode.rightChild != null) {//后继结点的左子树一定为空, 将其父结点的左孩子指向后继结点的右孩子
                    postParentRef.getValue().leftChild = postNode.rightChild;
                    postNode.rightChild = null; //置空相关引用，便于垃圾回收
                }
                //将删除的这个结点的左右子树的指针给到后继结点
                postNode.rightChild = delBinarySearchTree.rightChild;
                delBinarySearchTree.rightChild = null; //置空相关引用，便于垃圾回收
                postNode.leftChild = delBinarySearchTree.leftChild;
                delBinarySearchTree.leftChild = null; //置空相关引用，便于垃圾回收
            }
            //删除根或者比根小的，删除的结点在根的左边，需要找前驱结点
            else{
                RefObject<BinarySearchTree<T>> preParentRef = new RefObject<>(); //前驱结点的父结点
                BinarySearchTree<T> preNode = findMax(root.leftChild, preParentRef);

                if (parent != null) { //如果删除的是根结点 没有父结点
                    //判断要删除的结点是它父结点的左结点还是右结点，修改对应指针指向前驱结点
                    if (parent.data.compareTo(delBinarySearchTree.data) < 0) {
                        parent.rightChild = preNode;
                    } else {
                        parent.leftChild = preNode;
                    }
                }
                preParentRef.getValue().rightChild = null; //前驱结点因为要移走，所以置空其父结点的右孩子（前驱必定是其父的右孩子）
                if (preNode.leftChild != null) {//前驱结点的右子树一定为空, 将其父结点的右孩子指向前驱结点的左孩子
                    preParentRef.getValue().rightChild = preNode.leftChild;
                    preNode.leftChild = null; //置空相关引用，便于垃圾回收
                }

                if (delBinarySearchTree == root) {
                    //删除的是根 直接将交换值
                    delBinarySearchTree.data = preNode.data;
                }
                else {
                    //将删除的这个结点的左右孩子的指针给到前驱结点
                    preNode.rightChild = delBinarySearchTree.rightChild;
                    delBinarySearchTree.rightChild = null; //置空相关引用，便于垃圾回收
                    preNode.leftChild = delBinarySearchTree.leftChild;
                    delBinarySearchTree.leftChild = null; //置空相关引用，便于垃圾回收
                }
            }
        }
        //度为1的结点删除 将其父结点的孩子指向它的孩子
        else {
            BinarySearchTree<T> leftChild = delBinarySearchTree.leftChild;
            BinarySearchTree<T> child =  leftChild == null ? delBinarySearchTree.rightChild : leftChild;
            delBinarySearchTree.leftChild = null;  //置空相关引用，便于垃圾回收
            delBinarySearchTree.rightChild = null; //置空相关引用，便于垃圾回收
            if (parent.data.compareTo(child.data) < 0) {
                parent.rightChild = child;
            } else {
                parent.leftChild = child;
            }
        }
    }


    @Override
    public T getData() {
        return data;
    }

    @Override
    public void setData(T data) {
        this.data = data;
    }

    @Override
    public BinarySearchTree<T> getLeftChild() {
        return leftChild;
    }

    public void setLeftChild(BinarySearchTree<T> leftChild) {
        this.leftChild = leftChild;
    }

    @Override
    public BinarySearchTree<T> getRightChild() {
        return rightChild;
    }

    public void setRightChild(BinarySearchTree<T> rightChild) {
        this.rightChild = rightChild;
    }
}

 

遍历代码：

package com.nijunyang.algorithm.tree;

import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;

/**
 * @author: create by nijunyang
 * @date:2019/7/28
 */
public final class TreeUtil {

    private TreeUtil() {
    }


    /**
     * 构造二叉树
     * @param dataList
     * @param <T>
     * @return
     */
    public static <T> TreeNode<T> createBinaryTree(LinkedList<T> dataList) {
        TreeNode<T> node = null;
        if (dataList == null || dataList.isEmpty()) {
            return null;
        }
        T data = dataList.removeFirst();
        if (data != null) {
            node = new TreeNode(data);
            node.setLeftChild((createBinaryTree(dataList)));
            node.setRightChild((createBinaryTree(dataList)));
        }
        return node;
    }

    /**
     * 前序遍历 根 左子树 右子树
     * @param node
     */
    public static<N extends TreeNode<T>, T> void preOrderTraversal(N node) {
        if(node == null){
            return;
        }
        //遇根先输出，再去找左右
        System.out.print(node.getData());
        preOrderTraversal(node.getLeftChild());
        preOrderTraversal(node.getRightChild());
    }

    /**
     * 二叉树中序遍历 左子树 根 右子树
     * @param node   二叉树节点
     */
    public static<N extends TreeNode<T>, T> void inOrderTraversal(N node){
        if(node == null){
            return;
        }
        //先找左再输出根,再去找右
        inOrderTraversal(node.getLeftChild());
        System.out.print(node.getData());
        inOrderTraversal(node.getRightChild());
    }

    /**
     * 二叉树后序遍历  左子树 右子树 根
     * @param node   二叉树节点
     */
    public static<N extends TreeNode<T>, T> void postOrderTraversal(N node){
        if(node == null){
            return;
        }
        //先找左右，最后输出根
        postOrderTraversal(node.getLeftChild());
        postOrderTraversal(node.getRightChild());
        System.out.print(node.getData());
    }

    /**
     * 利用栈前序遍历二叉树
     * @param root
     */
    public static <N extends TreeNode<T>, T> void preOrderTraversalByStack(N root) {
        Stack<TreeNode<T>> stack = new Stack<>();
        TreeNode<T> node = root;
        while(node != null || !stack.isEmpty()) {
            //节点不为空，遍历节点，并入栈用于回溯
            while(node != null) {
                System.out.print(node.getData());
                stack.push(node);
                node = node.getLeftChild();
            }
            //没有左节点，弹出该栈顶节点（回溯），访问右节点
            if(!stack.isEmpty()) {
                node = stack.pop();
                node = node.getRightChild();
            }
        }
    }

    /**
     * 层次遍历
     * @param root
     * @param <T>
     */
    public static <N extends TreeNode<T>, T> void levelOrder(N root) {
        if (root == null) {
            return;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);  //入队
        while (!queue.isEmpty()) {
            TreeNode<T> node = queue.poll(); //取出
            if (node != null) {
                System.out.print(node.getData());
                queue.offer(node.getLeftChild());   //左孩子入队
                queue.offer(node.getRightChild());  //右孩子入队
            }
        }
    }
}

RefObject:

package com.nijunyang.algorithm.util;

/**
 * Description: 引用包装，用于去一个方法里面除开返回值之外，将其他额外需要的数据带出来
 * Created by nijunyang on 2020/4/20 10:26
 */
public class RefObject<E> {

    public RefObject() {
    }

    public RefObject(E value) {
        this.value = value;
    }


    private E value;

    public E getValue() {
        return value;
    }

    public void setValue(E value) {
        this.value = value;
    }
}