贪心算法顾名思义在一个贪字上面,它在解决某个问题的时候,总是先从眼前利益出发。也就是说只顾眼前,不顾大局,所以它是局部最优解。它的核心的就是局部最优推出全局最优。
比如公司只有一个会议室,明天有几场同样的重要的会议要开,怎么安排会议才能尽可能的多开会。
如果我们将所有会议的结束时间从小到大排序。然后从结束时间最小的开始选(局部最优),然后按照这个排序去遍历判断后面是开始时间是否在这之后,如果在则选它,如果不在,则判断下一个是否在。这样是否就能达到最终的最优解?可以尝试举反例来证明它结果的合法性。你会发现在这个场景中,似乎找不到比上述方案的更好的结果了。其实这就是一个贪心算法
贪心算法:
一定会有一个排序,这个就是我们所说的贪心策略,上面问题的策略就是以会议结束时间排序;不同的贪心策略出来结果是不一样,如果结果能被其他举例推翻,那就说明这个策略不合理。
贪心算法不是对所有问题都能得到整体最优解。但是如果经过大量证明成立之后,那么它就是一种高效的算法。
背包问题:
小偷去偷东西,背包只有5KG容量,现在有三个物品(不能分割,且各自只有一个),问小偷怎么拿才能带走最大价值的东西
A物品:1kg 6元
B物品:2kg 10元
C物品:4kg 12元
如果用贪心来看,这个问题我们似乎只能根据单价来排序了A单价6,B单价5,C单价3,那么我们按排序结果选择,就会选择AB,这个时候我们的价值是16,显然选择AC,价值是18,所以这个贪心策略很容易就被推翻了。
如此看来这个问题用贪心算法好像是无法解决了。
1.我们可以枚举(把所有情况的列出来)来看,那用到排列组合了,C33全部列出来看,数据小还可以,数据大了呢?
2.遍历所有,我们每个物品都有两个操作,选或者不选。
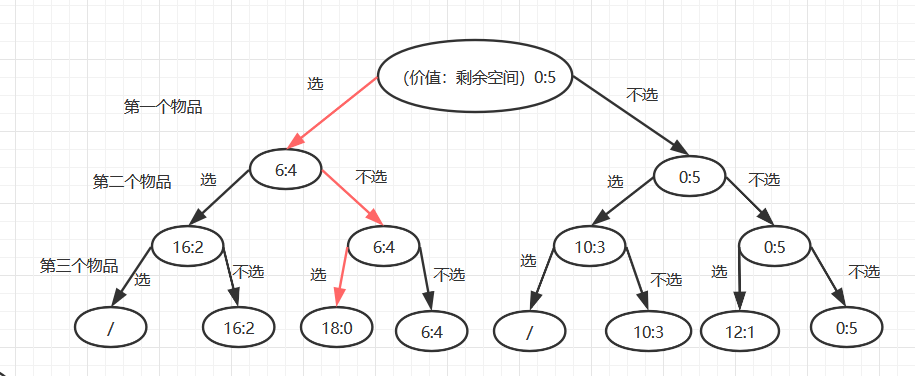
显然标红的那条路线就是我们最优的方案。每次在物品加进来的时候都会保存选择与不选择两种状态那么这样下去越到后面状态保存的就越多其实就是2^n次。
3.动态规划
问将背包按1kg来逻辑分割,可以整理出来如下表格
|
1kg |
2kg |
3kg |
4kg |
5kg |
|
|
加入物品A |
6 |
6 |
6 |
6 |
6 |
|
加入物品B |
6 |
10 |
10+6=16 |
16 |
16 |
|
加入物品C |
6 |
10 |
16 |
16 |
12+6=18 |
首先这个表格是从上往下一行一行的来看,前面的会影响后面的。第一行为什么全是6,因为这个是后只有A加入,第二行加入B,这个时候前面有一行A的数据了,所以要一起考虑A了.....
从第二行开始看下具体的逻辑,加入物品B,当背包容量1kg的时候,B是装不进去的,但是前面的数据1kg的时候可以装A,所以价值是6;背包容量2kg这个时候刚好可以装B,比较下B和之前的价值,发现10是大于6的,显然我们装B;背包容量3kg的时候,显然装完B,还剩1kg,因此可以一起装就是价值16
第三行的1 2 3列数据同理,C装不下但是可以装A和B;当背包4kg时,可以装下C,但是C的价值才12,而且装完C之后没有容量了,然而我们不装C的时候 价值都是16了,显然我们不装C;当背包5kg的时候,这个时候可以装C,价值12,装完还剩1kg,前面1kg的时候可以装A,因此12+6=18的价值。
这个表格最后的数据就是我们所需要的最优结果。
能装的时候 每次和上面的比较,大我就装,否则就不装。这个过程和先装谁没有关系,比如下面先装C再装B最后A,按照上面的逻辑一样的可以得到这个结果
|
1kg |
2kg |
3kg |
4kg |
5kg |
|
|
加入物品C |
0 |
0 |
0 |
12 |
12 |
|
加入物品B |
0 |
10 |
10 |
12 |
12 |
|
加入物品A |
6 |
10 |
16 |
16 |
18 |
上面这个推导过程总结起来就是------状态转移方程
上面的这个表的数据是不是就是一个二维数组,可以得到如下公式
(注意:为了方便代码实现,数组下标均从1开始)
Math.max(money[i - 1] + freeMoney , notHaveCurrent)
freeMoney = result[i - 1][currentW - weight[i - 1]];
notHaveCurrent = result[i - 1][currentW];
int money[] ={6,10,12}
int weight[] = {1,2,4};
result[][] 结果二维数组
currentW: 当前背包容量
freeMoney : 装完当前物品,余下空间的价值
notHaveCurrent: 不要加入物品的价值,也就是前面一次的价值
money[i - 1]:当前的物品的价值
下面就用代码来实现这个逻辑:
public static int dynamicProgramming() { int[] money ={10,6,12}; int[] weight = {2,1,4}; int w = 5; //包容量 int count = 3; int result[][] = new int[count+1][w+1]; //容量是从1开始,都扩大一位防止越界,放置物品也从一开始,因为第一次也要取前一次的数据,保证前一次有默认数据 for (int i = 1; i <= count; i++) { //依次装物品 for (int currentW = 1; currentW <= w; currentW++) { //背包容量依次增加 if (weight[i - 1] <= currentW) { //当前物品的容量小于当前背包重量表示可以装进去 int freeMoney = result[i - 1][currentW - weight[i - 1]]; //装完当前物品,余下空间的价值 int notHaveCurrent = result[i - 1][currentW]; //不要当前物品的价值,也就是前面一次的价值 result[i][currentW] = Math.max(money[i - 1] + freeMoney, notHaveCurrent); } else { //不能装当前 取前一次 result[i][currentW] = result[i - 1][currentW]; } } } return result[count][w]; }
在动态规划中最重要的就是找到状态转移方程。可以借助状态转移表,来找到状态转移方程,比如上面的表格,找到这个方程之后,基本上就可以用代码来实现了。
动态规划是每次都会把当前情况下的最优解计算出来,层层递推,下一层的最优解都是基于它上一次结果存下来的,所以最后一个结果就一定是最优解。而贪心是指关心局部,不管后面,上面会议,第一个会议决定了,后面其实也就决定了。