赫夫曼树在基础数据结构里也是一个难点,所以趁在家我把我课下和张同学写的报告提一些出来,稍微详细的写一下。
基本概念:
赫夫曼树又称为最优树,是一类带权路径长度最短的树。它具有n个叶子结点(每个结点的权值为wi) 的二叉树不止一棵,但在所有的这些二叉树中,必定存在一棵WPL值最小的树,称这棵树为Huffman树(或称最优树)。在赫夫曼树中,权值最大的结点离根最近,权值最小的结点离根最远。它的基本概念如下:
树的路径指从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径;路径长度指路径上的分支数目;树的路径长度指从树根到每个结点的路径长度之和;带权路径长度指从结点到树根之间的路径长度与结点上权的乘积;树的带权路径长度(WPL)指树中所有叶子结点的带权路径长度之和。
Huffman编码算法流程:
1.根据给定的n个权值(w1, w2, …, wn)构成n棵二叉树的集合F={T1, T2, …, Tn},其中每棵二叉树Ti中只有一个带树为Ti的根结点;
2.在F中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树,且置其根结点的权值为其左右子树权值之和;
3.在F中删除这两棵树,同时将新得到的二叉树加入F中;
4.重复2, 3,直到F只含一棵树为止。
拓展应用:Huffman压缩文件
原理:计算机存储文件都是以二进制流的形式;Huffman编码通过出现字节的频率的不同,用0和1组成的编码串代替原字节。例如某字符串中字节AA出现了100次,字节BB出现了5次,压缩字符串大小需要AA尽可能用短的编码代替,BB用相对长一点的编码代替,即可有效缩短了文件整体的bit数。
Huffman编码例子:
1. 给定一串字符串如下图;

2. 统计字符种类,得到五种字符;

3. 统计每种字符出现个数,获得权值;

4. 每次选取最小的两个节点构建二叉树;

5. 置其根结点的权值为其左右子树权值之和;
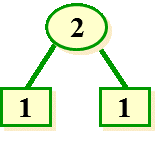
6. 删除表中两个已经添加过的叶子节点,将根节点置入表中,并回到第4步;(规定左节点小于右节点,当权值相等时比较字符在ASCII表中顺序)

7. 规定左孩子为0,右孩子为1,构建哈弗曼编码表,构建完成后如下图;



接下来是构建编码的代码,写了些注释应该可以比较容易理解:
#include <iostream> #include <string> #include <cstring> using namespace std; const int MaxW = 9999; //假设结点权值不超过9999 //定义huffman树结点类 class HuffNode { public: int weight; //权值 int parent; //父结点下标 int leftchild; //左孩子下标 int rightchild; //右孩子下标 }; //定义huffman树类 class HuffMan { private: void MakeTree(); //建树,私有函数,被公有函数调用 void SelectMin(int pos, int *s1, int *s2); //从1到pos的位置找出权值最小的两个结点,结点下标存在s1和s2中 public: int len; //结点数量 int lnum; //叶子数量 HuffNode *huffTree; //huffman树,用数组表示 string * huffCode; //每个字符对应的huffman编码 void MakeTree(int n,int wt[]); //公有函数,被主函数main调用 void Coding(); //公有函数,被主函数main调用 void Destroy(); }; //构建huffman树 void HuffMan::MakeTree(int n,int wt[]) //参数是叶子结点数量和叶子权值 {//公有函数,对外接口 int i; lnum = n; len = 2*n-1; huffTree = new HuffNode[2*n]; huffCode = new string [lnum+1]; //位置从1开始计算 //huffCode实质是个二维字符数组,第i行表示第i个字符对应的编码 //huffman树huffTree初始化 for(i=1;i<=len;i++) huffTree[i].weight = wt[i-1]; //第0号不用,从1开始编号 for(i=1;i<=len;i++) { if(i>n) huffTree[i].weight=0; //前n个结点是叶子,已经设值 huffTree[i].parent = 0; huffTree[i].leftchild = 0; huffTree[i].rightchild=0; } MakeTree(); //调用私有函数建树 } void HuffMan::SelectMin(int pos,int *s1,int *s2) //找出最小的两个权值的下标 //函数采用地址传递的方法,找出的两个下标保存在s1和s2中 { int w1,w2,i; w1=w2=MaxW; //初始化w1和w2为最大值,在比较中会被实际的权值替换 *s1=*s2=0; for(i=1;i<=pos;i++) //对结点数组进行搜索 { if(huffTree[i].weight < w1 && huffTree[i].parent == 0) { //如果i结点的权值小于w1,且第i结点是未选择的结点(父亲为0) w2 = w1; //把w1,s1保存到w2,s2,即原来的第一最小值变成第二最小值(不理解?) *s2 = *s1; w1 = huffTree[i].weight; //把i结点的权值和下标保存到w1,s1,作为第一最小值 *s1=i; } else if(huffTree[i].weight < w2 && huffTree[i].parent == 0) { w2=huffTree[i].weight;*s2=i; } //否则如果i结点的权值小于w2,且i结点是未选中的,把i结点的权值和下标保存到w2和s2,作为第二最小值 } } void HuffMan::MakeTree() {//私有函数,被公有函数调用 int i,s1,s2; //构造huffman树HuffTree的n-1个非叶子结点 for(i=lnum+1;i<=len;i++) { SelectMin(i-1,&s1,&s2); //找出两个最小权值的下标放入s1和s2中 for(i = lnum+1;i <= len;i++) { SelectMin(i-1,&s1,&s2); //找出两个最小权值的下标放入s1,s1 huffTree[s1].parent = i; //将找出的两棵权值最小的字数合并为一颗子树 huffTree[s2].parent = i; //结点s1,s2的父亲设为i huffTree[i].leftchild = s1; //i的左右孩子为s1,s2 huffTree[i].rightchild = s2; huffTree[i].weight = huffTree[s1].weight + huffTree[s2].weight; //i的权值等于s1,s2权值和 } } } //销毁huffman树 void HuffMan::Destroy() { len = 0; lnum = 0; delete []huffTree; delete []huffCode; } //huffman编码 void HuffMan::Coding() { char *cd; int i,c,f,start; //求n个叶结点的huffman编码 cd = new char[lnum]; //分配求编码的工作空间 cd[lnum-1] = '�'; for (i=1;i<=lnum;++i) //逐个字符求huffman编码 { start = lnum-1; //编码结束符位置 //严蔚敏老师的书P147第二个for循环有参考 for(c = i,f = huffTree[i].parent; f != 0; c = f, f = huffTree[f].parent) //从叶子到根逆向球编码 if(huffTree[f].leftchild == c) { cd[--start] = '0'; } else { cd[--start] = '1'; } huffCode[i] = new char[lnum-start]; //为第i各字符编码分配空间 huffCode[i].assign(&cd[start]); //把cd中从start到末尾的编码复制到huffCode中 } delete []cd; //释放工作空间 } //主函数 int main() { int t,n,i,j; int wt[800]; HuffMan myHuff; cin>>t; for(i=0;i<t;i++) { cin>>n; for(j=0;j<n;j++) cin>> wt[j]; myHuff.MakeTree(n,wt); myHuff.Coding(); for (j=1;j<=n;j++) { cout<< myHuff.huffTree[j].weight<<'-'; //输出各权值 cout<< myHuff.huffCode[j]<<endl; //输出各编码 } myHuff.Destroy(); } return 0; }
下一篇是关于赫夫曼解码,也会稍微详细的解释一下。
作者:Nathaneko