T1:

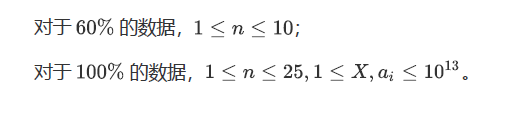
分析:
如果x小的话,就直接背包。这道题中n很小,60%可以直接3^10暴搜,25的呢?明显是折半嘛。
先搜前一半的物品,用map记录能拼凑出的种类数,再搜后一半物品,直接查询统计答案即可。

#include<bits/stdc++.h> using namespace std; #define N 50 #define ll long long #define ri register int ll a[N],b[N],maxn[N],n,x,ans=0,n1,n2; map<ll,int> mp; int get(ll x) { int cnt=0; while(x){ cnt+=(x&1); x>>=1; } return cnt; } void dfs1(int now,ll tot) { if(now>n1) { mp[tot]++; return ; } if(tot>x) return ; dfs1(now+1,tot+a[now]); dfs1(now+1,tot+b[now]); dfs1(now+1,tot); } void dfs2(int now,ll tot) { if(now>n2) { ans+=mp[x-tot]; return ; } if(tot>x) return ; dfs2(now+1,tot+a[now]); dfs2(now+1,tot+b[now]); dfs2(now+1,tot); } int main() { freopen("building.in","r",stdin); freopen("building.out","w",stdout); scanf("%d%lld",&n,&x); n1=(n+1)>>1,n2=n; for(ri i=1;i<=n;++i) scanf("%lld",&a[i]),b[i]=(1<<get(a[i])); dfs1(1,0); dfs2(n1+1,0); printf("%lld ",ans); }
T2:

分析:
简化一下题意:找出有向图中所有环,每个环内的边取min,所有环中的min取max。
很努力地想如何O(n)找到有向图中的所有环,但还是不知道。。。
对于最大值最小很显然可以换一个思路:二分!
二分一个值mid,如果存在一个环使得环上的所有边权都大于mid,就说明这个值不合法。
所以只需要挑边权小于等于mid的边跑一边,判断有没有环即可。
然后我脑残地用n^2去判环。。。导致只拿了个暴力分。。。
O(n)地判环可以tarjan,也可以拓扑。(这道题中优选tarjan,拓扑还要重新建边)

#include<bits/stdc++.h> using namespace std; #define ri register int #define M 300005 #define N 200005 int n,m,to[M],nex[M],head[N],w[M],vis[N],tot=0; int top=0,Ti=0,dfn[N],low[N],stk[N],flag[N]; void add(int a,int b,int c) { to[++tot]=b; nex[tot]=head[a]; head[a]=tot; w[tot]=c; } bool tarjan(int u,int k) { dfn[u]=low[u]=++Ti; stk[++top]=u; flag[u]=1; for(ri i=head[u];i;i=nex[i]){ int v=to[i]; if(w[i]<=k) continue; if(!dfn[v]){ if(tarjan(v,k)) return true; low[u]=min(low[u],low[v]); } else if(flag[v]) { low[u]=min(low[u],dfn[v]); return true; } } if(dfn[u]==low[u]){ do{ int tmp=stk[top]; flag[tmp]=0; }while(stk[top--]!=u); } return false; } int main() { freopen("pestc.in","r",stdin); freopen("pestc.out","w",stdout); scanf("%d%d",&n,&m); int a,b,c,mx=0; for(ri i=1;i<=m;++i) scanf("%d%d%d",&a,&b,&c),add(a,b,c),mx=max(mx,c); int l=0,r=mx+1,ans=0; while(l<r){ int mid=(l+r)>>1,fl=1; memset(dfn,0,sizeof(dfn)); memset(low,0,sizeof(low)); memset(flag,0,sizeof(flag)); Ti=0; top=0; for(ri i=1;i<=n;++i) if(!dfn[i]){ if(tarjan(i,mid)) { fl=0; break; } } if(fl) r=mid,ans=mid; else l=mid+1; } printf("%d ",ans); } /* 4 5 3 4 8 1 4 9 3 1 6 4 2 1 2 4 8 3 4 1 2 3 2 1 1 2 3 2 3 1 4 9 13 1 2 3 2 3 2 3 4 5 4 1 9 1 5 6 5 6 7 6 1 8 3 7 6 7 3 3 8 7 9 7 8 11 8 9 12 9 7 13 */
T3:



分析:
我不会dsu on tree,也不会线段树合并。。。
但这道题其实可以利用天天爱跑步的思想做。
求小于,等于,大于一个值显然可以维护一颗值域树状数组(只需要单点修改,区间查询),也就是开一个桶。
设u的两个子节点v1和v2。
当v1遍历完后,桶中保留了v1及其所有子节点的信息。
这时我们遍历v2,将v2子树中的信息也加入桶里,那么统计v2的贡献时明显会统计到v1子树中的,怎么办呢?
只需要在将v2子树中信息加入前记录一下原来的,然后加入后再两者相减即可。

#include<bits/stdc++.h> using namespace std; #define N 200005 #define ri register int int n,sum[N],a[N],b[N],mn[N],sq[N],mx[N]; vector<int> e[N]; int query(int x)//维护值域树状数组 { int ans=0; while(x>0){ ans+=sum[x]; x-=(x&-x); } return ans;//记得return 值。。。 } void modify(int x) { while(x<=n){ sum[x]+=1; x+=(x&-x); } } int get(int l,int r) { return query(r)-query(l-1); } void dfs(int u,int ff) { int pre_min=get(1,a[u]-1);//先求出非其子树的贡献 int pre_seq=get(a[u],a[u]); int pre_max=get(a[u]+1,n); for(ri i=0;i<e[u].size();++i){ int v=e[u][i]; if(v==ff) continue; dfs(v,u); } mn[u]=get(1,a[u]-1)-pre_min;//再除去非其子树的影响 sq[u]=get(a[u],a[u])-pre_seq; mx[u]=get(a[u]+1,n)-pre_max; modify(a[u]); } int main() { freopen("ginkgo.in","r",stdin); freopen("ginkgo.out","w",stdout); scanf("%d",&n); int x; for(ri i=2;i<=n;++i) scanf("%d",&x),e[i].push_back(x),e[x].push_back(i); for(ri i=1;i<=n;++i) scanf("%d",&a[i]),b[i]=a[i]; sort(b+1,b+1+n); int num=unique(b+1,b+1+n)-b-1;//离散化 for(ri i=1;i<=n;++i) a[i]=lower_bound(b+1,b+1+num,a[i])-b; swap(n,num);//!! dfs(1,0); for(ri i=1;i<=num;++i) printf("%d %d %d ",mn[i],sq[i],mx[i]); } /* 5 1 1 3 3 0 0 1 2 0 */

