题意略.
显然,我们为了排列数 O(1) 查,先预处理阶乘和阶乘的逆元。
然后,看到 0 <= n <= 20 , 发现邻接表存图十分的 美妙 。
推荐用这个很像状压的存图方式:
For(i,1,m){ //M:Total of Edge
scanf("%d%d",&u,&v);
edge[u]|=1<<v;
edge[v]|=1<<u;
}
现在我们来考虑转移,
定义 dp [ fettle ] 为 “已取fettle状态个点” 同时 “已知与fettle相邻点集中的每个点的位置为p” 时的方案数 (其中 fettle 为一个独立集)
我们枚举下一个将要加入 fettle 中的 i 。显然,i 不与 fettle 中的任一个点相连。
由于我们已经知道了 p, 那么 i 就在 p 中第一个未被占领的位置上。
对于与 i 相连 , 同时不与 fettle 中的任一个点相连的点集 , 它们可以占领任意其余未被占领位置。
例:
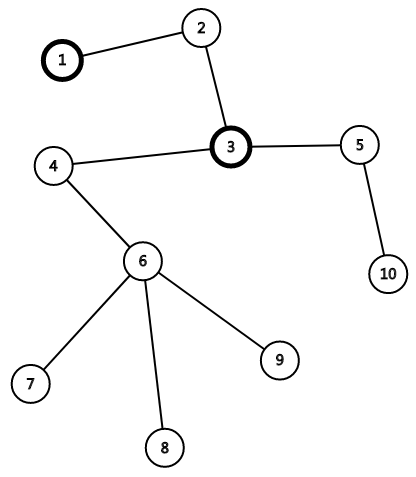
fettle 中 有 1 、3 两个点,下一个被加入的只能是 6 号。
由于题面中算法随机,所以 6、7、8 号点则可以随便占领
所以得到转移方程:
多占领一个 i 的方案数 = 原来的方案数 * 只有剩下点乱搞的方案数。
然后,暴力枚举 fettle 转移即可 。
关于时间复杂度与优化:
把每个点是否和点i相邻压成一个二进制数a[i],然后对于所有i∈mask把a[i]取或就可以得到所有和mask里的点相邻的点,这样整个算法的时间复杂度就是O(n*2^n)的 ——神犇题解
然后,交上去,就过了