Github项目地址:https://github.com/MokouTyan/suduku_131700101
【2019.09.20】更新:代码经过Code Quality Analysis工具的分析并消除所有的警告。
【2019.09.21】更新:使用性能分析工具Studio Profiling Tools来找出代码中的性能瓶颈。
【2019.09.21】更新:想到了“即使题目是唯一解,但同时每个格子有多种可能性”的情况,新增函数check,以及格式化输出规范
【2019.09.22】更新:更新了Github上的代码,可以测试了
【2019.09.23】更新:新增全局变量change与chess_count,在循环中如果不发生改变即产生双解,并结束本表盘的执行
【2019.09.24】更新:实现对“-m”,“-n”,"-i"、"-o"的判断
【2019.09.25】更新:《构建之法》前三章读后感:https://www.cnblogs.com/mokou/p/11582103.html
尚未完成内容:
PSP表格
| Personal Software Process Stages | 预估耗时 | 实际耗时 | |
|---|---|---|---|
| Planning | 计划 | 1小时 | 5分钟 |
| Estimate | 这个任务需要多少时间 | 26小时 | 24小时 |
| Development | 开发 | 5小时 | 4小时 |
| Analysis | 需求分析 (包括学习新技术) | 2小时 | 1小时 |
| Design Spec | 生成设计文档 | 2小时 | 1小时 |
| Design Review | 设计复审 | 2小时 | 1小时 |
| Coding Standard | 代码规范 | 30分钟 | 1小时 |
| Design | 具体设计 | 30分钟 | 30分钟 |
| Coding | 具体编码 | 5小时 | 2小时 |
| Code Review | 代码复审 | 2小时 | 4小时 |
| Test | 测试(自我测试,修改代码,提交修改) | 1小时 | 3小时 |
| Reporting | 报告 | 1小时 | 2小时 |
| Test Repor | 测试报告 | 1小时 | 30分钟 |
| Postmortem | 事后总结, 并提出过程改进计划 | 1小时 | 2小时 |
| Improvement Plan | 过程改进计划 | 1小时 | 2小时 |
| 合计 | 26小时 | 24小时 |
视频介绍所用思路
最近因为有自己的视频在做,所以有点忙不过来,这次的视频也是花了两小时赶出来的,以后如果太忙了可能不会做视频啦见谅(咕咕咕)

因为这个方法是自己想的,我没有依据可以证明“唯一的解必须由唯一的可能性推导而出”,所以我也不知道对不对
(我的舍友是认为,即使所有的格子有一个以上的可能性数量,也可以推出唯一的解来)
视频里是我的思路,如果看不清表盘填的数字可以在视频右下角切换清晰度
不论是inside函数还是outside函数,他们的执行顺序都是横纵宫
(其实这三个顺序无所谓的,但是三个都要去执行)
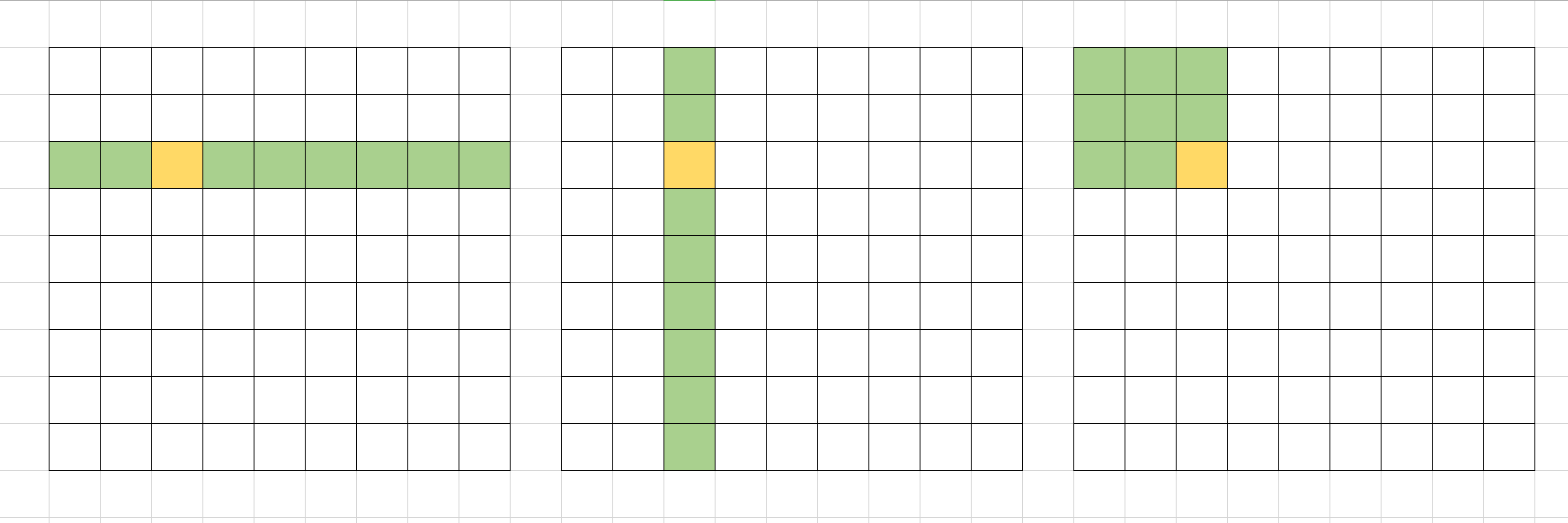
黄色是传入函数的位置,而绿色是所要检测的格子
源代码解释
全局变量介绍:
void check();
//记录棋盘上的标记点
bool sign[10][10][10];
//记录标记点的可能性剩余个数
int sign_count[10][10];
//记录棋盘
int checkerboard[10][10];
//记录类型
int type;
int small_sign[10];
//用于记录是否有变化
bool change;
int chess_count;
初始化表盘:
在CMD中输入type和棋盘个数后进入循环
在开始处理数据前先进行表盘重置化
每个位置的可能性初期都为9个(根据输入type大小而定)
表盘上所有数字为0(代表空)
sign第三个[]内的0号位都为False,其意义是还未填入数字
每个位置上的第一格到第九格可能性都存在(标为True)
void reset()
{
for (int i = 1; i < type + 1; i++)
{
for (int j = 1; j < type + 1; j++)
{
//假设每个位置都有type种可能
sign_count[i][j] = type;
//每个位置都是空
checkerboard[i][j] = 0;
//每个位置未曾填写
sign[i][j][0] = false;
//假设每个位置的type种可能都是可实现的
for (int k = 1; k < type + 1; k++)
{
sign[i][j][k] = true;
}
}
}
return;
}
inside函数解释:
我用的第一个函数,我称为inside函数
从头到尾遍历,向函数传递格子的位置
它会检测当前位置横、纵、九宫格有没有数字的格子
如果有数字存在并且该数字可能性还未去掉
便把该格子上的相同数字的可能性去掉,同时可能性数量-1
如果当可能性等于1时,立即写入数字
//查出所有空缺的可能性(位置上还没有数字)
//此时是扣除所在位置的可能性
int inside(int x, int y)
{
//排除横纵向可能性
int remove;
for (int i = 1; i < type + 1; i++)
{
//如果检测位置存在数
if (sign[x][i][0])
{
remove = checkerboard[x][i];
//则这个空位不能出现相同数字
//防止sign_count被误减去,前面先判断是不是已经变否了,未变否才变否
if (sign[x][y][remove])
{
sign[x][y][remove] = false;
//可能性-1
sign_count[x][y]--;
}
if (sign_count[x][y] == 1 && !sign[x][y][0])
{
write(x, y);
return 0;
}
}
}
for (int i = 1; i < type + 1; i++)
{
if (sign[i][y][0])
{
remove = checkerboard[i][y];
if (sign[x][y][remove])
{
sign[x][y][remove] = false;
sign_count[x][y]--;
}
if (sign_count[x][y] == 1 && !sign[x][y][0])
{
write(x, y);
return 0;
}
}
}
//宫格判断
if (type == 4 || type == 6 || type == 8 || type == 9)
{
int beginx, beginy;
int xplus, yplus;
switch (type)
{
case 4:
xplus = 2;
yplus = 2;
break;
case 6:
xplus = 2;
yplus = 3;
break;
case 8:
xplus = 4;
yplus = 2;
break;
case 9:
xplus = 3;
yplus = 3;
break;
}
beginx = ((x - 1) / xplus)*xplus + 1;
beginy = ((y - 1) / yplus)*yplus + 1;
for (int i = beginx; i < beginx + xplus; i++)
{
for (int j = beginy; j < beginy + yplus; j++)
{
if (sign[i][j][0])
{
if (sign[x][y][(checkerboard[i][j])])
{
sign[x][y][(checkerboard[i][j])] = false;
sign_count[x][y]--;
}
if (sign_count[x][y] == 1 && !sign[x][y][0])
{
write(x, y);
return 0;
}
}
}
}
}
//经过上面的判断,如果该位置只剩下一种可能性,那么执行write()
return 0;
}
write函数:
写入数字的时候会把位置上的标记改为存在数字(该位置sign第三个的[0]=True)
可能性数量变为0(该位置的sign_count=0;)
防止被二次修改
//填入确定值
int write(int x, int y)
{
//这个位置标记为存在数字
change = true;
chess_count--;
sign[x][y][0] = true;
sign_count[x][y] = 0;
//填入数字
for (int i = 1; i < type + 1; i++)
{
if (sign[x][y][i])
{
checkerboard[x][y] = i;
break;
}
}
outside(x, y);
return 0;
}
在写入数字的函数结束前
此时调用第二个函数,我称为outside函数
进行横纵宫的外部检查,将这个数字影响扩出去,当这个格子的“横纵宫”检查完成后等于说就成为一张新的表盘了
outside函数:
传入所写数字的位置
将它的横纵九宫格上所有格子上的相同数字的可能性去掉
当其他位置可能性数量为1的时候
再次立即调动write函数
//去除所填位置的横纵九宫格所有同数可能性(位置上刚填入数字)
//此时是扣除所填位置的横纵九宫格的其他位置可能性
int outside(int x, int y)
{
//remove是当前位置填入的数字
int remove = checkerboard[x][y];
for (int i = 1; i < type + 1; i++)
{
if (!sign[x][i][0] && sign[x][i][remove])
{
sign[x][i][remove] = false;
sign_count[x][i]--;
if (sign_count[x][i] == 1 && !sign[x][i][0])
{
write(x, i);
}
}
}
for (int i = 1; i < type + 1; i++)
{
if (!sign[i][y][0] && sign[i][y][remove])
{
sign[i][y][remove] = false;
sign_count[i][y]--;
if (sign_count[i][y] == 1 && !sign[i][y][0])
{
write(i, y);
}
}
}
//宫格判断
if (type == 4 || type == 6 || type == 8 || type == 9)
{
int beginx, beginy;
int xplus, yplus;
switch (type)
{
case 4:
xplus = 2;
yplus = 2;
break;
case 6:
xplus = 2;
yplus = 3;
break;
case 8:
xplus = 4;
yplus = 2;
break;
case 9:
xplus = 3;
yplus = 3;
break;
}
beginx = ((x - 1) / xplus)*xplus + 1;
beginy = ((y - 1) / yplus)*yplus + 1;
for (int i = beginx; i < beginx + xplus; i++)
{
for (int j = beginy; j < beginy + yplus; j++)
{
if (!sign[i][j][0] && sign[i][j][remove])
{
sign[i][j][remove] = false;
sign_count[i][j]--;
if (sign_count[i][j] == 1 && !sign[i][j][0])
{
write(i, j);
}
}
}
}
}
return 0;
}
经常会出现这样的情况,(write)填入第一个数字→(第一个outside)检查第一个数字的横向,刚好找到可能性数量为1的存在→(write)填入第二个数字→(第二个outside)检查第二个数字的横纵宫,减去外部的可能性,没有出现可能性数量刚好为1的点(此时return回调用自己write,再return回上一个outside)→(第一个outside)重新返回第一个数字的函数内,继续检查完第一个数字的横纵宫
(也正是因为这样所以write里面要对填入的格子进行锁死,防止第一个outside会遍历 第二个及其以后的outside 会再次填入)
write和outside就这样子互相嵌套调用,每当outside函数彻底完成后(即直到当前的outside是由 inside调用的write所调用的)是相当于生成一个新的表盘
check函数:
想到一种特殊情况
假如在同一排内有三个空格,他们的可能性分别为“12”,“23”,“12”
尽管它们都有一个以上的选项,但是中间这一格必须填3,因为它只在这一排出现过一次
所以要检查同一排内是否有只有一个可能性种类的情况出现
void check()
{
//检查每一横
for (int i = 1; i < type + 1; i++)
{
for (int j = 1; j < type + 1; j++)
{
small_sign[j] = 0;
}
for (int j = 1; j < type + 1; j++)
{
if (!sign[i][j][0])
{
for (int k = 1; k < type + 1; k++)
{
if (sign[i][j][k])
{
small_sign[k]++;
}
}
}
}
for (int k = 1; k < type + 1; k++)
{
if (small_sign[k] == 1)
{
for (int j = 1; j < type + 1; j++)
{
if (sign[i][j][k] && !sign[i][j][0])
{
//这个位置标记为存在数字
chess_count--;
change = true;
sign[i][j][0] = true;
sign_count[i][j] = 0;
checkerboard[i][j] = k;
outside(i, j);
}
}
}
}
}
//检查每一纵
for (int j = 1; j < type + 1; j++)
{
for (int i = 1; i < type + 1; i++)
{
small_sign[i] = 0;
}
for (int i = 1; i < type + 1; i++)
{
if (!sign[i][j][0])
{
for (int k = 1; k < type + 1; k++)
{
if (sign[i][j][k])
{
small_sign[k]++;
}
}
}
}
for (int k = 1; k < type + 1; k++)
{
if (small_sign[k] == 1)
{
for (int i = 1; i < type + 1; i++)
{
if (sign[i][j][k] && !sign[i][j][0])
{
//这个位置标记为存在数字
chess_count--;
change = true;
sign[i][j][0] = true;
sign_count[i][j] = 0;
checkerboard[i][j] = k;
outside(i, j);
}
}
}
}
}
}
主函数:
int main(int argc, char *argv[])
{
int n;
FILE* fp1;
FILE* fp2;
type = atoi(argv[2]);
n = atoi(argv[4]);
char* InputName = argv[6];
char* OutputName = argv[8];
//以只读方式打开文件
fp1 = fopen(InputName, "r");
if (fp1 == NULL) //
return -1;
//fscanf(fp1, "%d%d", &type,&n);
//打开output.txt,并立即关闭,意义为清空文本内容
fp2 = fopen(OutputName, "w");
if (fp2 == NULL) //
return -1;
fclose(fp2);
while (n > 0)
{
//重置棋盘
reset();
//输入棋盘
for (int i = 1; i < type + 1; i++)
{
for (int j = 1; j < type + 1; j++)
{
//cin >> checkerboard[i][j];
fscanf(fp1, "%d", &checkerboard[i][j]);
if (checkerboard[i][j] != 0)
{
sign[i][j][0] = true;
sign_count[i][j] = 0;
chess_count--;
}
}
}
//棋盘上以填格子的数量,当它等于零的时候棋盘被填满
chess_count = type * type;
change = true;
while (chess_count != 0 && change)
{
//先默认棋盘不发生变化
change = false;
//找出空缺位置
for (int k = 0; k < 2; k++)
{
for (int i = 1; i < type + 1; i++)
{
for (int j = 1; j < type + 1; j++)
{
if (!sign[i][j][0])
{
inside(i, j);
}
}
}
}
check();
}
//以只写方式打开文件
fp2 = fopen(OutputName, "a");
if (fp2 == NULL)
return -1;
bool sign_complete = true;
if (chess_count != 0) sign_complete = false;
for (int i = 1; i < type + 1; i++)
{
for (int j = 1; j < type + 1; j++)
{
//cout << checkerboard[i][j];
fprintf(fp2, "%d", checkerboard[i][j]);
if (j != type)
{
fprintf(fp2, " ");
//cout << ' ';
}
}
if (n != 1 && i == type && sign_complete)
{
//cout << "
";
fprintf(fp2, "
");
}
else if (n != 1 && i == type && !sign_complete)
{
//cout << "
无法再确定地填入任何一格
因此棋盘中有空位
";
fprintf(fp2, "
无法再确定地填入任何一格
因此棋盘中有空位
");
}
else if (n == 1 && i == type && sign_complete) {}
else if (n == 1 && i == type && !sign_complete)
{
//cout << "
无法再确定地填入任何一格
因此棋盘中有空位";
fprintf(fp2, "
无法再确定地填入任何一格
因此棋盘中有空位");
}
else
{
//cout << "
";
fprintf(fp2, "
");
}
}
//cout << '
';//
//fprintf(fp2, "
");
n--;
fclose(fp2);
}
fclose(fp1);
}
代码调试阶段
Code Quality Analysis检查结果:
测试样例结果:
九宫格展示:
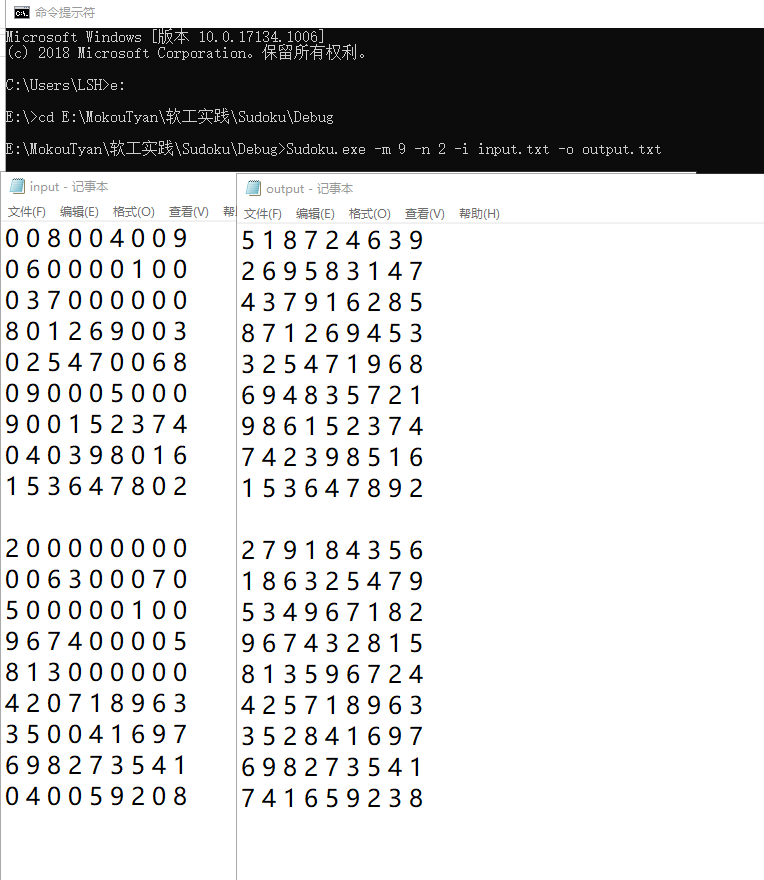
其他类型宫格展示:


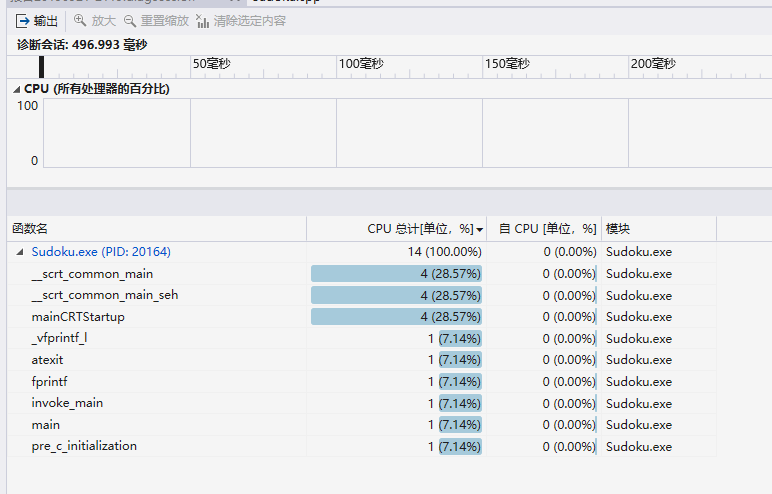
性能分析工具Studio Profiling Tools分析结果
分别是上面的四个四宫格,三个六宫格,两个九宫格题目的分析结果
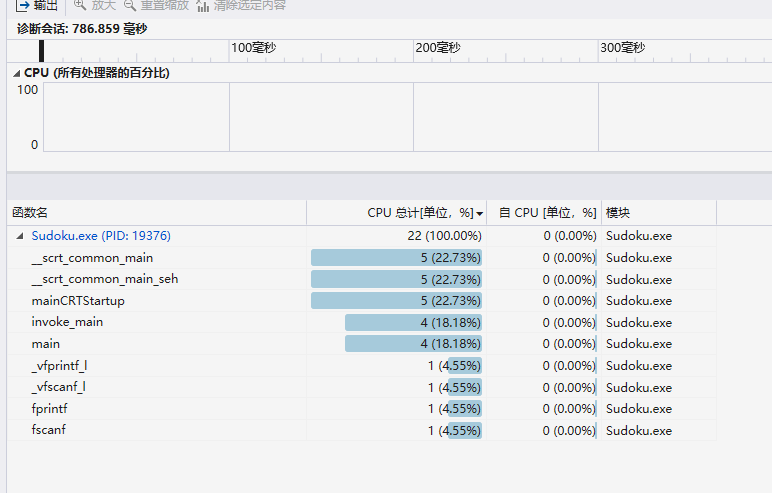

总结
这个解决方案只能解决唯一解的数独问题
面对多个解的数独棋盘,这个方法可能解不完整,会有空缺位置
因为都是自己的思考,在完成这道题的时候完全按照自己思路,所以并不一定正确
完成后去查看过别人的代码,他们的程序也都很有道理,我还是要学习一个~
