二维线段树一般用线段树套线段树写,当然也可以用四叉树写
树套树,顾名思义,外层树的每个节点都是一棵树。
题目地址:https://www.luogu.org/problemnew/show/U22582
首先要了解的知识:
-
线段树
-
标记永久化
标记永久化:
参考https://www.cnblogs.com/Hallmeow/p/8004676.html
简单地讲一下,如果要详细了解的话可以百度。
一般线段树实现区间修改我们用的是懒惰标记,但是遇到一些主席树,树套树等毒瘤数据结构,懒惰标记就显得很麻烦了。
这时候就需要用到标记永久化。这样就可以省掉一堆pushup和pushdown了,就可以可持久化了
原理:
在查询的时候把途经的节点上的标记对答案的影响加上,省掉了下推的过程。
实现:
修改:
比如现在要把区间[(L,R)]全部数加v。
到达被[(L,R)]完全包含的节点(节点所代表区间在[(L,R)]内)时,就把节点的标记加上v,然后return。
把完全包含[(L,R)]的区间([(L,R)]在节点所代表区间内)(一路下来的所有区间)的sum加上(v*(R-L))。
询问:
因为修改时对下面的节点完全没有影响,所以要一路累积标记的影响,直到查询区间与当前节点区间完全重合。
答案就是sum+ad(一路累积标记的影响的总和)*查询区间长度
注意:
因为打标记的时候是节点区间与目标区间完全重合,所以要注意向下递归时要用特殊的方式(求最大值的时候不用)。
代码实现:
这里给个结构体封装的标记永久化线段树,方便后面树套树的实现。
彩蛋:经本人实测,标记永久化线段树比普通线段树快得多,可以用来卡常
#include<cstdio>
#define int ll
#define ll long long
#define gc getchar
int gi(){int x=0,f=0;char c=gc();while(c<'0'||'9'<c){if(c=='-')f=!f;c=gc();}while('0'<=c&&c<='9'){x=x*10+c-48;c=gc();}return f?(-x):x;}
using namespace std;
#define N 100001
int n,q;
struct xds{
#define Z int m=(l+r)>>1
#define ls rt<<1
#define rs rt<<1|1
int s[N*3],tag[N*3];
void build(int l,int r,int rt){
if(l==r){s[rt]=gi();return;}
Z;build(l,m,ls);build(m+1,r,rs);
s[rt]=s[ls]+s[rs];
}
void upd(int L,int R,int v,int l,int r,int rt){
s[rt]+=v*(R-L+1);
if(L==l&&r==R){
tag[rt]+=v;
return;
}
Z;
//注意!!!!!!!!!!!!!!!!!!!!
if(R<=m)upd(L,R,v,l,m,ls);
else{
if(L>m)upd(L,R,v,m+1,r,rs);
else upd(L,m,v,l,m,ls),upd(m+1,R,v,m+1,r,rs);
}
}
int qh(int L,int R,int l,int r,int rt,int ad){
if(L==l&&r==R)return s[rt]+ad*(r-l+1);
Z;ad+=tag[rt];
if(R<=m)return qh(L,R,l,m,ls,ad);
else{
if(L>m)return qh(L,R,m+1,r,rs,ad);
else return qh(L,m,l,m,ls,ad)+qh(m+1,R,m+1,r,rs,ad);
}
}
}s;
signed main(){
n=gi();q=gi();
s.build(1,n,1);
int p,x,y;
while(q--){
p=gi();x=gi();y=gi();
if(p==1)s.upd(x,y,gi(),1,n,1);
else printf("%lld
",s.qh(x,y,1,n,1,0));
}
}
树套树实现方法:
一般是先按x轴建外层树,然后在按y轴建树。
内层树更普通线段树一样,外层树每次都更新节点。
为了方便,一般树套树用标记永久化来写。
而在区间加&&区间求和中,就必须用标记永久化。
代码请在最后的完整代码中找。
图解:
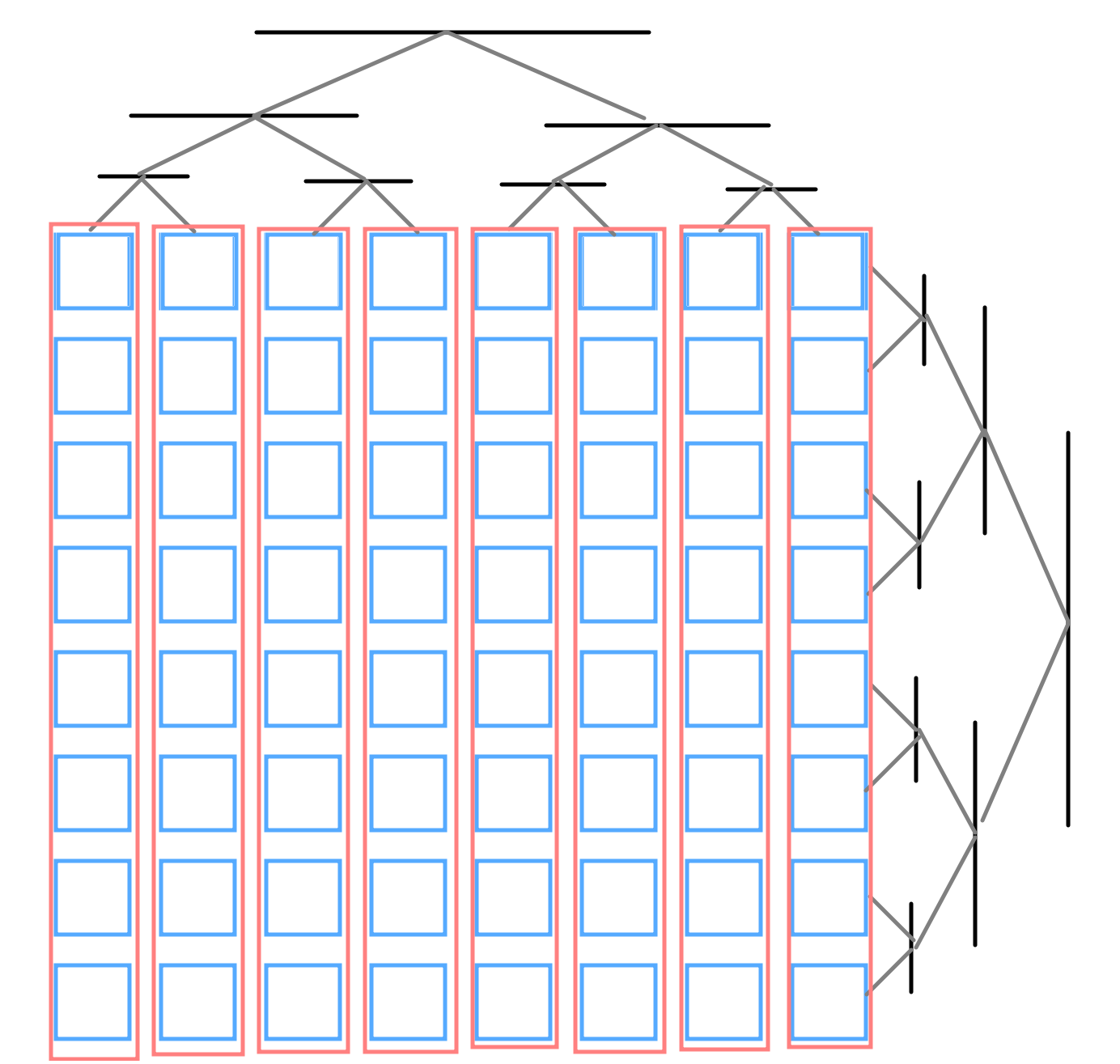
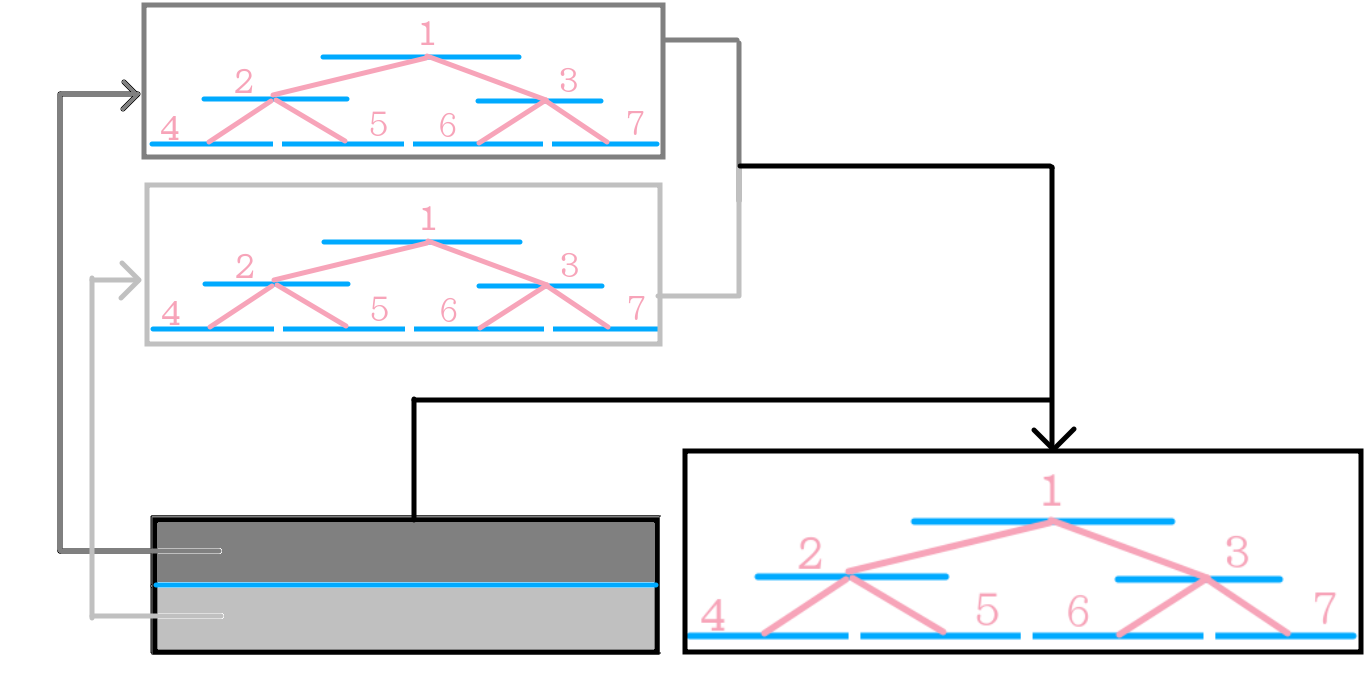
第二张倒过来看233
建树
内层线段树没有区别。
按照第二张图解,外层线段树对应每个节点等于它的左右儿子的对应节点的和。
比如节点1等于两棵子树对应的节点1的和。
更新
不管是区间更新和点更新,标记永久化都比较方便。
内层和原来一样。
外层的更新就是直接更新节点对应的内层线段树。
下图中绿色的矩形区域就是目标区域,就是外层树中每个绿色节点的内层树的每个红色节点所代表的区域。
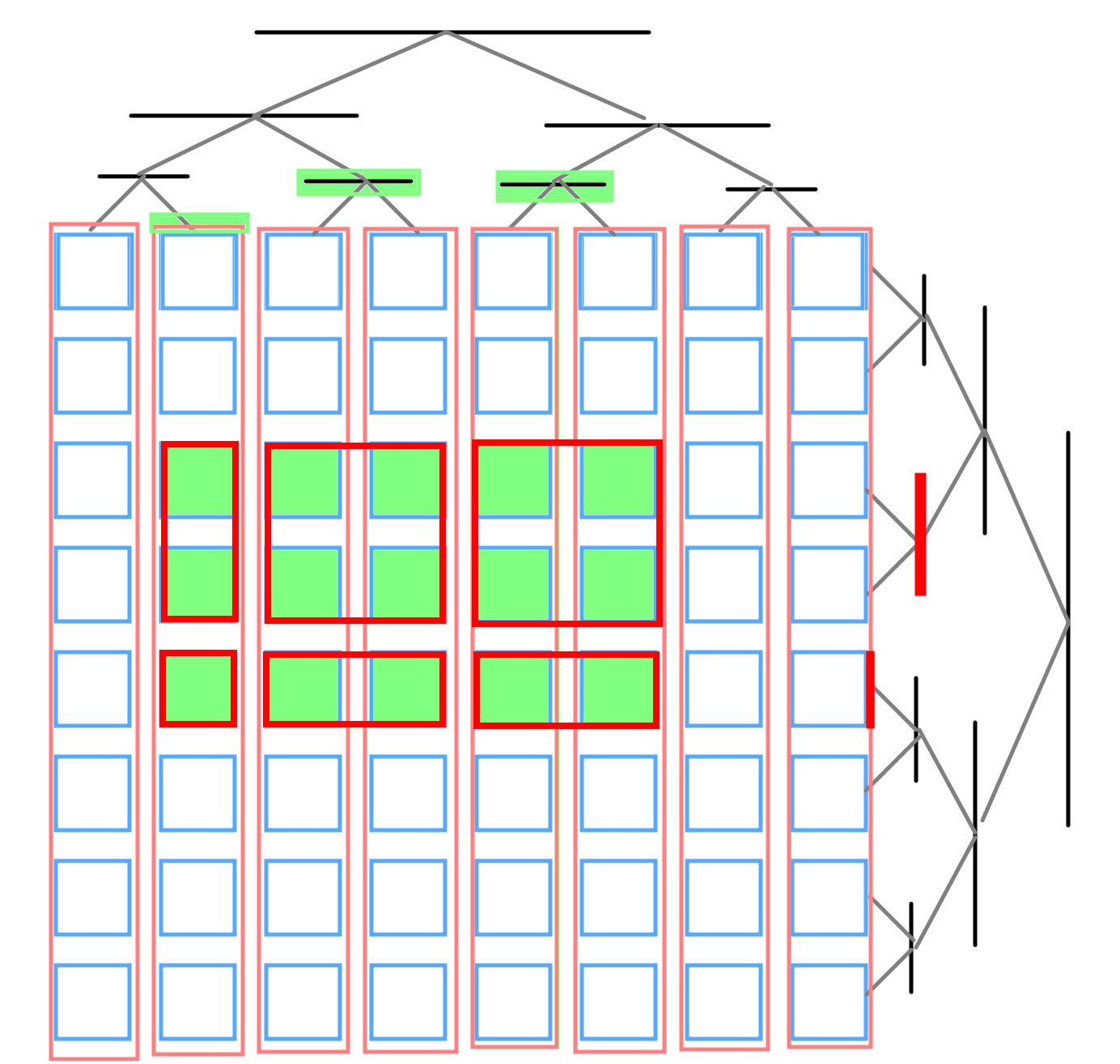
查询
上图中绿色的矩形区域就是要求的区域,相当于外层树中每个绿色节点的内层树的每个红色节点所代表的区域的和。
注意:
单点查询的树套树可以不用标记永久化(不建议),用二维数组来记录而不用结构体,建树时比较方便。
结构体方便理解和差错,建议写结构体版本。
以下也有给出二维数组来记录的版本。
不管什么推荐用标记永久化,至少方便而且代码跑起来会快很多,本来树套树就是一个很暴力的数据结构。
代码:
#include<cstdio>
#define gc getchar
int gi(){int x=0,f=0;char c=gc();while(c<'0'||'9'<c){if(c=='-')f=!f;c=gc();}while('0'<=c&&c<='9'){x=x*10+c-48;c=gc();}return f?(-x):x;}
using namespace std;
#define N 2010
int D,S,q;
struct xds{//内层(标记永久化)
#define Z int m=(l+r)>>1
#define ls rt<<1
#define rs rt<<1|1
int s[N*4],tag[N*4];
void build(int l,int r,int rt){//内层建树
if(l==r){s[rt]=gi();return;}
Z;build(l,m,ls);build(m+1,r,rs);
s[rt]=s[ls]+s[rs];
}
void upd(int L,int R,int v,int l,int r,int rt){//内层修改
s[rt]+=v*(R-L+1);
if(L==l&&r==R){
tag[rt]+=v;
return;
}
Z;
if(R<=m)upd(L,R,v,l,m,ls);
else{
if(L>m)upd(L,R,v,m+1,r,rs);
else upd(L,m,v,l,m,ls),upd(m+1,R,v,m+1,r,rs);
}
}
int qh(int L,int R,int l,int r,int rt,int ad){
if(L==l&&r==R)return s[rt]+ad*(r-l+1);
Z;ad+=tag[rt];
if(R<=m)return qh(L,R,l,m,ls,ad);
else{
if(L>m)return qh(L,R,m+1,r,rs,ad);
else return qh(L,m,l,m,ls,ad)+qh(m+1,R,m+1,r,rs,ad);
}
}
}s[N*4],tag[N*4];
void mg(xds& o,xds& lc,xds& rc,int l,int r,int rt){//外层节点更新(pushup)
o.s[rt]=lc.s[rt]+rc.s[rt];
if(l==r)return;
Z;mg(o,lc,rc,l,m,ls);mg(o,lc,rc,m+1,r,rs);
}
void build(int l,int r,int rt){//外层建树
if(l==r){
s[rt].build(1,S,1);
return;
}
Z;build(l,m,ls);build(m+1,r,rs);
mg(s[rt],s[ls],s[rs],1,S,1);
}
void upd(int x,int y,int xx,int yy,int v,int l,int r,int rt){//外层修改
s[rt].upd(y,yy,v*(xx-x+1),1,S,1);
if(x==l&&r==xx){
tag[rt].upd(y,yy,v,1,S,1);
return;
}
Z;
if(xx<=m)upd(x,y,xx,yy,v,l,m,ls);
else{
if(x>m)upd(x,y,xx,yy,v,m+1,r,rs);
else upd(x,y,m,yy,v,l,m,ls),upd(m+1,y,xx,yy,v,m+1,r,rs);
}
}
int qh(int x,int y,int xx,int yy,int l,int r,int rt,int ad){//查询(求和)
if(x==l&&r==xx)return s[rt].qh(y,yy,1,S,1,0)+ad*(r-l+1);
Z;ad+=tag[rt].qh(y,yy,1,S,1,0);
if(xx<=m)return qh(x,y,xx,yy,l,m,ls,ad);
else{
if(x>m)return qh(x,y,xx,yy,m+1,r,rs,ad);
else return qh(x,y,m,yy,l,m,ls,ad)+qh(m+1,y,xx,yy,m+1,r,rs,ad);
}
}
int main(){
D=gi();S=gi();q=gi();
build(1,D,1);
int p,x,y,xx,yy;
while(q--){
p=gi();x=gi();y=gi();xx=gi();yy=gi();
if(p==1)printf("%d
",qh(x,y,xx,yy,1,D,1,0));
else upd(x,y,xx,yy,gi(),1,D,1);
}
}
是不是感觉这板子比别人的短很多。
练习(感觉都比例题容易):
1. UVA11297 Census
题意:
给一个n*n的矩阵
操作1:修改点(x,y)的值为v
操作2:查询区域(x1,y1,x2,y2)中的最大值
题解:
就是把求和的更新操作改为求最大值的更新操作。
另附一种方便建树时更新的做法(直接用二维数组来存外层和内层线段树):
代码
2.P3437 [POI2006]TET-Tetris 3D
题意:
给定一个矩阵,初始每个位置上的元素都是0,每次选择一个子矩形,将这个子矩形内的值修改为这个子矩形内的最大值+h,求最终所有位置上的最大值
题解:
最大值的标记永久化比求和的容易的多。
而且不用建树。
代码
3.HDU 4819 Mosaic
题意:
给定一个n*n的矩阵,每次给定一个子矩阵区域(x,y,l),求出该区域内的最大值(A)和最小值(B),输出(A+B)/2,并用这个值更新矩阵[x,y]的值
题解:
和例题1没什么太大区别
代码
4.Poj 2155 Matrix
题意:
一个n*n的矩阵一开始全是0
操作C:将区域(x1,y1,x2,y2)中的数翻转(0的变1,1的变0)
操作Q:查询位置(x,y)的数是多少
题解:
区间修改,单点查询
标记永久化的优势充分地显示出来。
代码
5.Vijos 1512 SuperBrother打鼹鼠
题意:
矩阵大小为n*n
操作1:点(x,y)新出现k只鼹鼠
操作2:查询区域(x1,y1,x2,y2)中鼹鼠的总数
题解:
单点修改,区间求和。
试一试用四叉树写