5.1 蒙特卡洛预测
分为两种:First-Visit MC和Every-Visit MC,前者用的更多。后者用于函数近似和Eligibility Traces

5.2 蒙特卡洛评估action value
如果没有模型(即不知道每个a会得到什么样的s),则应该使用action value而不是state value
5.3 蒙特卡洛控制
这里要用到广义策略迭代方法。即交替更新价值函数和策略。经典方法有两个假设:任意起始点和无穷片段。先去掉后一个解释,就是利用GPI中的思想,不再等待完整的评估之后再改进策略,而是每走一步都更新actoin value

5.4 去掉任意起始点的假设
分为两种方法:on-policy和off-policy。前者在学习和最终应用的策略是同一个。最常见的是$epsilon$-soft策略

5.5 off-policy预测:重要性取样
定义两个策略:目标策略$pi$和行为策略$mu$。对于目标策略中任意可能出现的动作(s,a),行为策略中必须出现。
对于策略$pi$,产生某状态-动作序列的概率是:

那么对两个不同策略来说,它们的比值为:
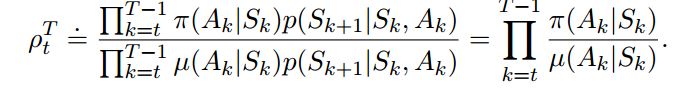
为表达方便,我们把多个episode首尾相接成单个episode。得出目标策略的状态价值函数的表达式:
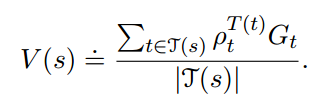
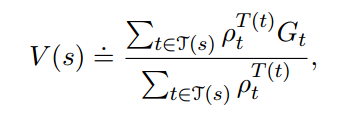
前者称为普通的重要性取样,后者称为加权的重要性取样。前者是无偏的,但是方差较大甚至无限。后者有偏(但渐进于0),但方差较小且有限。后者用的更多。
5.6 增量实现(策略评估,计算v)
对式子:
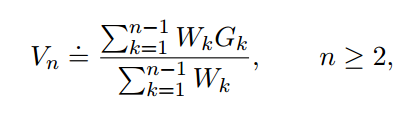
我们给出增量实现的版本:
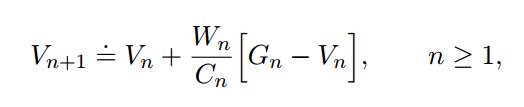
![]()
程序如下:

5.7 off-policy蒙特卡洛控制:在上面的基础上增加一行更新策略

5.8 Return-Specific重要性取样
对于$gamma$特别小的来说,普通重要性采样将导致较大误差。考虑一个长度为100的序列,当$gamma=0$时,事实上return只包含第一个reward,但是重要性采样比例却会考虑进整个100的序列。因此需要修正:
![]()