In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation
DZY loves Fibonacci numbers very much. Today DZY gives you an array consisting of n integers: a1, a2, ..., an. Moreover, there are m queries, each query has one of the two types:
- Format of the query "1 l r". In reply to the query, you need to add Fi - l + 1 to each element ai, where l ≤ i ≤ r.
- Format of the query "2 l r". In reply to the query you should output the value of
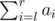 modulo 1000000009 (109 + 9).
modulo 1000000009 (109 + 9).
Help DZY reply to all the queries.
The first line of the input contains two integers n and m (1 ≤ n, m ≤ 300000). The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 109) — initial array a.
Then, m lines follow. A single line describes a single query in the format given in the statement. It is guaranteed that for each query inequality 1 ≤ l ≤ r ≤ n holds.
For each query of the second type, print the value of the sum on a single line.
4 4
1 2 3 4
1 1 4
2 1 4
1 2 4
2 1 3
17
12
After the first query, a = [2, 3, 5, 7].
For the second query, sum = 2 + 3 + 5 + 7 = 17.
After the third query, a = [2, 4, 6, 9].
For the fourth query, sum = 2 + 4 + 6 = 12.
官方题解:
As we know, 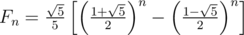
Fortunately, we find that 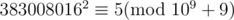
So, 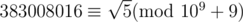
With multiplicative inverse, we find,
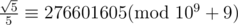
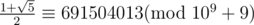
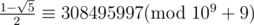
Now, 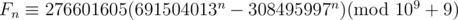
As you see, we can just maintain the sum of a Geometric progression 
This is a simple problem which can be solved with segment tree in  .
.
这道题是Fibonacci数列通项公式的应用,比较经典。至少我是不可能想到斐波那契数列与等比数列有任何关联。还有一点,在程序内层循环中,快速幂的时间复杂度是不容忽视的(估计是线段树写抽了),这里既然公比恒定,可先与处理一下。
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #include<cmath> using namespace std; #define MAXN 310000 #define MAXT 1210000 #define MOD 1000000009 #define lch (now<<1) #define rch (now<<1^1) void nextInt(int &x) { char ch; x=0; while (ch=getchar(),ch>'9'||ch<'0'); do x=x*10+ch-'0'; while (ch=getchar(),ch<='9'&&ch>='0'); } int n,m; typedef long long qword; int num[MAXN]; qword val1,val2,val3,val4,val3_n,val4_n,mod; qword val3_pow[MAXN],val4_pow[MAXN]; qword pow_mod(qword x,qword y,int mod) { qword ret=1; while (y) { if (y&1)ret=ret*x%mod; x=x*x%mod; y>>=1; } return ret; } struct node { int l,r; qword sum; qword inc3,inc4; }tree[MAXT]; inline void update_sum_3(int now,int inc3) { qword temp; temp=inc3*(val3_pow[tree[now].r-tree[now].l+1]-1)%MOD*val3_n%MOD; // temp=(temp+MOD)%MOD; tree[now].sum=(tree[now].sum+temp)%MOD; } inline void update_sum_4(int now,int inc4) { qword temp; temp=inc4*(val4_pow[tree[now].r-tree[now].l+1]-1)%MOD*val4_n%MOD; temp=(-temp+MOD)%MOD; tree[now].sum=(tree[now].sum+temp)%MOD; } inline void down(int now) { if (tree[now].l==tree[now].r) { if (tree[now].inc3) { tree[now].inc3=0; } if (tree[now].inc4) { tree[now].inc4=0; } return ; } if (tree[now].inc3) { qword temp; tree[lch].inc3=(tree[lch].inc3+tree[now].inc3)%MOD; // tree[lch].inc3%=MOD; update_sum_3(lch,tree[now].inc3); tree[rch].inc3+=temp=val3_pow[tree[lch].r-tree[lch].l+1]*tree[now].inc3%MOD; tree[rch].inc3%=MOD; update_sum_3(rch,temp); tree[now].inc3=0; } if (tree[now].inc4) { qword temp; tree[lch].inc4+=tree[now].inc4; tree[lch].inc4%=MOD; update_sum_4(lch,tree[now].inc4); tree[rch].inc4+=temp=val4_pow[tree[lch].r-tree[lch].l+1]*tree[now].inc4%MOD; tree[rch].inc4%=MOD; update_sum_4(rch,temp); tree[now].inc4=0; } } inline void update(int now) { if (tree[now].l!=tree[now].r) tree[now].sum=(tree[lch].sum+tree[rch].sum)%MOD; } void init() { /*//{{{ int i; for (i=1;i<MOD;i++) { if ((qword)i*i%MOD==5) { val1=i; break; } } cout<<val1<<endl; for (i=1;i<MOD;i++) { if ((qword)i*5%MOD==val1) { val2=i; break; } } cout<<val2<<endl; for (i=1;i<MOD;i++) { if ((qword)i*2%MOD-1==val1) { val3=i; break; } } cout<<val3<<endl; for (i=1;i<MOD;i++) { if ((qword)i*2-1==(-val1+MOD)%MOD) { val4=i; break; } } cout<<val4<<endl;//}}}*/ val1=383008016;//sqrt(5) val2=276601605;//sqrt(5)/5 val3=691504013;//(1+sqrt(5))/2 val4=308495997;//(1-sqrt(5))/2 int i; qword temp=val3; val3_pow[0]=1; for (i=1;i<MAXN;i++) { val3_pow[i]=val3_pow[i-1]*val3%MOD;; } val4_pow[0]=1; for (i=1;i<MAXN;i++) { val4_pow[i]=val4_pow[i-1]*val4%MOD; } val3_n=pow_mod(val3-1,MOD-2,MOD); val4_n=pow_mod(val4-1,MOD-2,MOD); //fib(n)=val2*(val3^n-val4^n); } void build_tree(int now,int l,int r) { tree[now].l=l; tree[now].r=r; if (l==r) { tree[now].sum=num[l]; return ; } int mid=(l+r)/2; build_tree(lch,l,mid); build_tree(rch,mid+1,r); update(now); } void add_val(int now,int l,int r,int rk) { if (tree[now].l==l&&tree[now].r==r) { qword temp; temp=val2*val3%MOD*val3_pow[rk]%MOD; tree[now].inc3=(tree[now].inc3+temp)%MOD; update_sum_3(now,temp); temp=val2*val4%MOD*val4_pow[rk]%MOD; tree[now].inc4=(tree[now].inc4+temp)%MOD; update_sum_4(now,temp); return ; } down(now); int mid=(tree[now].l+tree[now].r)>>1; if (r<=mid) { add_val(lch,l,r,rk); update(now); return ; } if (mid<l) { add_val(rch,l,r,rk); update(now); return ; } add_val(lch,l,mid,rk); add_val(rch,mid+1,r,rk-l+mid+1); update(now); } //ok qword query(int now,int l,int r) { if (tree[now].l==l&&tree[now].r==r) { return tree[now].sum; } down(now); int mid=(tree[now].l+tree[now].r)>>1; if (r<=mid) return query(lch,l,r); if (mid<l) return query(rch,l,r); return (query(lch,l,mid)+query(rch,mid+1,r))%MOD; } int main() { freopen("input.txt","r",stdin); freopen("output.txt","w",stdout); //scanf("%d%d",&n,&m); nextInt(n); nextInt(m); int i,j,k,x,y,z; init(); for (i=1;i<=n;i++) nextInt(num[i]); build_tree(1,1,n); while (m--) { nextInt(x); nextInt(y); nextInt(z); if (x==1) { add_val(1,y,z,0); }else { printf("%I64d ",query(1,y,z)); } } }