哈希表(Hash Table)是一种特殊的数据结构,它最大的特点就是可以快速实现查找、插入和删除。因为它独有的特点,Hash表经常被用来解决大数据问题,也因此被广大的程序员所青睐。为了能够更加灵活地使用Hash来提高我们的代码效率,今天,我们就谈一谈Hash的那点事。
1. 哈希表的基本思想
我们知道,数组的最大特点就是:寻址容易,插入和删除困难;而链表正好相反,寻址困难,而插入和删除操作容易。那么如果能够结合两者的优点,做出一种寻址、插入和删除操作同样快速容易的数据结构,那该有多好。这就是哈希表创建的基本思想,而实际上哈希表也实现了这样的一个“夙愿”,哈希表就是这样一个集查找、插入和删除操作于一身的数据结构。
2. 哈希表的相关基本概念
在介绍Hash之前,首先我们要搞明白几个概念:
哈希表(Hash Table):也叫散列表,是根据关键码值(Key-Value)而直接进行访问的数据结构,也就是我们常用到的map。
哈希函数:也称为是散列函数,是Hash表的映射函数,它可以把任意长度的输入变换成固定长度的输出,该输出就是哈希值。哈希函数能使对一个数据序列的访问过程变得更加迅速有效,通过哈希函数数据元素能够被很快的进行定位。
哈希表和哈希函数的标准定义:
-
若关键字为k,则其值存放在f(k)的存储位置上。由此,不需比较便可直接取得所查记录。称这个对应关系f为哈希函数,按这个思想建立的表为哈希表。
设所有可能出现的关键字集合记为U(简称全集)。实际发生(即实际存储)的关键字集合记为K(|K|比|U|小得多)。
散列方法是使用函数h将U映射到表T[0..m-1]的下标上(m=O(|U|))。这样以U中关键字为自变量,以h为函数的运算结果就是相应结点的存储地址。从而达到在O(1)时间内就可完成查找。
其中:
① h:U→{0,1,2,…,m-1} ,通常称h为哈希函数(Hash Function)。哈希函数h的作用是压缩待处理的下标范围,使待处理的|U|个值减少到m个值,从而降低空间开销。
② T为哈希表(Hash Table)。
③ h(Ki)(Ki∈U)是关键字为Ki结点存储地址(亦称散列值或散列地址)。
④ 将结点按其关键字的哈希地址存储到哈希表中的过程称为散列(Hashing)
1)冲突:
两个不同的关键字,由于散列函数值相同,因而被映射到同一表位置上。该现象称为冲突(Collision)或碰撞。发生冲突的两个关键字称为该散列函数的同义词(Synonym)。
2)安全避免冲突的条件:
最理想的解决冲突的方法是安全避免冲突。要做到这一点必须满足两个条件:
①其一是|U|≤m
②其二是选择合适的散列函数。
这只适用于|U|较小,且关键字均事先已知的情况,此时经过精心设计散列函数h有可能完全避免冲突。
3)冲突不可能完全避免
通常情况下,h是一个压缩映像。虽然|K|≤m,但|U|>m,故无论怎样设计h,也不可能完全避免冲突。因此,只能在设计h时尽可能使冲突最少。同时还需要确定解决冲突的方法,使发生冲突的同义词能够存储到表中。
4)影响冲突的因素
冲突的频繁程度除了与h相关外,还与表的填满程度相关。
设m和n分别表示表长和表中填入的结点数,则将α=n/m定义为散列表的装填因子(Load Factor)。α越大,表越满,冲突的机会也越大。通常取α≤1。
3. 哈希表的实现方法
我们之前说了,哈希表是一个集查找、插入和删除操作于一身的数据结构。那这么完美的数据结构到底是怎么实现的呢?哈希表有很多种不同的实现方法,为了实现哈希表的创建,这些所有的方法都离不开两个问题——“定址”和“解决冲突”。
在这里,我们通过详细地介绍哈希表最常用的方法——取余法(定值)+拉链法(解决冲突),来一起窥探一下哈希表强大的优点。
取余法大家一定不会感觉陌生,就是我们经常说的取余数的操作。
拉链法是什么,“拉链”说白了就是“链表数组”。我这么一解释,大家更晕了,啥是“链表数组”啊?为了更好地解释“链表数组”,我们用下图进行解释:图中的主干部分是一个顺序存储结构数组,但是有的数组元素为空,有的对应一个值,有的对应的是一个链表,这就是“链表数组”。比如数组0的位置对应一个链表,链表有两个元素“496”和“896”,这说明元素“496”和“896”有着同样的Hash地址,这就是我们上边介绍的“冲突”或者“碰撞”。但是“链表数组”的存储方式很好地解决了Hash表中的冲突问题,发生冲突的元素会被存在一个对应Hash地址指向的链表中。实际上,“链表数组”就是一个指针数组,每一个指针指向一个链表的头结点,链表可能为空,也可能不为空。

说完这些,大家肯定已经理解了“链表数组”的概念,那我们就一起看看Hash表是如何根据“取余法+拉链法”构建的吧。
将所有关键字为同义词的结点链接在同一个链表中。若选定的散列表长度为m,则可将散列表定义为一个由m个头指针组成的指针数组T[0..m-1]。凡是散列地址为i的结点,均插入到以T[i]为头指针的单链表中。T中各分量的初值均应为空指针。在拉链法中,装填因子α可以大于1,但一般均取α≤1。
举例说明拉链法的执行过程,设有一组关键字为(26,36,41,38,44,15,68,12,6,51),用取余法构造散列函数,初始情况如下图所示: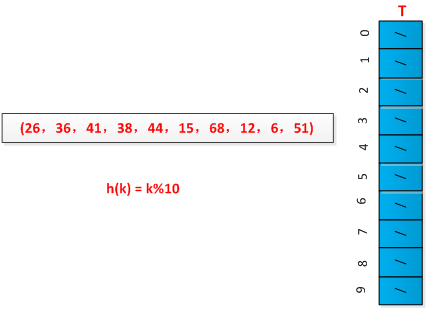
最终结果如下图所示:

理解了Hash表的创建,那根据建立的Hash表进行查找就很容易被理解了。
查找操作,如果理解了插入和删除,查找操作就比较简单了,令待查找的关键字是x,也可分为几种情况:
1)x所属的Hash地址未被占用,即不存在与x相同的Hash地址关键字,当然也不存在x了;
2)x所属的Hash地址被占用了,但它所存的关键不属于这个Hash地址,与1)相同,不存在与x相同Hash地址的关键字;
3)x所属的Hash地址被占用了,且它所存的关键属于这个Hash地址,即存在与x相同sHash地址的关键字,只是不知这个关键字是不是x,需要进一步查找。
由此可见,Hash表插入、删除和插入操作的效率都相当的高。
思考一个问题:如果关键字是字符串怎么办?我们怎么根据字符串建立Hash表?
通常都是将元素的key转换为数字进行散列,如果key本身就是整数,那么散列函数可以采用keymod tablesize(要保证tablesize是质数)。而在实际工作中经常用字符串作为关键字,例如身姓名、职位等等。这个时候需要设计一个好的散列函数进程处理关键字为字符串的元素。参考《数据结构与算法分析》第5章,有以下几种处理方法:
方法1:将字符串的所有的字符的ASCII码值进行相加,将所得和作为元素的关键字。设计的散列函数如下所示:
int hash(const string& key,int tablesize) { int hashVal = 0; for(int i=0;i<key.length();i++) hashVal += key[i]; return hashVal % tableSize; }
此方法的缺点是不能有效的分布元素,例如假设关键字是有8个字母构成的字符串,散列表的长度为10007。字母最大的ASCII码为127,按照方法1可得到关键字对应的最大数值为127×8=1016,也就是说通过散列函数映射时只能映射到散列表的槽0-1016之间,这样导致大部分槽没有用到,分布不均匀,从而效率低下。
方法2:假设关键字至少有三个字母构成,散列函数只是取前三个字母进行散列。设计的散列函数如下所示:
int hash(const string& key,int tablesize) { //27 represents the number of letters plus the blank return (key[0]+27*key[1]+729*key[2])%tablesize; }
该方法只是取字符串的前三个字符的ASCII码进行散列,最大的得到的数值是2851,如果散列的长度为10007,那么只有28%的空间被用到,大部分空间没有用到。因此如果散列表太大,就不太适用。
方法3:借助Horner's 规则,构造一个质数(通常是37)的多项式,(非常的巧妙,不知道为何是37)。计算公式为:key[keysize-i-1]*37i, 0<=i<keysize求和。设计的散列函数如下所示:
int hash(const string & key,int tablesize) { int hashVal = 0; for(int i =0;i<key.length();i++) hashVal = 37*hashVal + key[i]; hashVal %= tableSize; if(hashVal<0) //计算的hashVal溢出 hashVal += tableSize; return hashVal; }
该方法存在的问题是如果字符串关键字比较长,散列函数的计算过程就变长,有可能导致计算的hashVal溢出。针对这种情况可以采取字符串的部分字符进行计算,例如计算偶数或者奇数位的字符。
4. 哈希表“定址”的方法
其实常用的“定址”的手法有“五种”:
1)直接定址法
很容易理解,key=Value+C;这个“C"是常量。Value+C其实就是一个简单的哈希函数。
2)除法取余法
key=value%C
3)数字分析法
这种蛮有意思,比如有一组value1=112233,value2=112633,value3=119033,针对这样的数我们分析数中间两个数比较波动,其他数不变。那么我们取key的值就可以是key1=22,key2=26,key3=90。
4)平方取中法
5)折叠法
举个例子,比如value=135790,要求key是2位数的散列值。那么我们将value变为13+57+90=160,然后去掉高位“1”,此时key=60,哈哈,这就是他们的哈希关系,这样做的目的就是key与每一位value都相关,来做到“散列地址”尽可能分散的目地。
影响哈希查找效率的一个重要因素是哈希函数本身。当两个不同的数据元素的哈希值相同时,就会发生冲突。为减少发生冲突的可能性,哈希函数应该将数据尽可能分散地映射到哈希表的每一个表项中。
5. 哈希表“解决冲突”的方法
Hash表解决冲突的方法主要有以下两种:
1)开放地址法
如果两个数据元素的哈希值相同,则在哈希表中为后插入的数据元素另外选择一个表项。当程序查找哈希表时,如果没有在第一个对应的哈希表项中找到符合查找要求的数据元素,程序就会继续往后查找,直到找到一个符合查找要求的数据元素,或者遇到一个空的表项。
开放地址法包括线性探测、二次探测以及双重散列等方法。其中线性探测法示意图如下:

散列过程如下图所示:

2)链地址法
将哈希值相同的数据元素存放在一个链表中,在查找哈希表的过程中,当查找到这个链表时,必须采用线性查找方法。
6. 哈希表“定址”和“解决冲突”之间的权衡
虽然哈希表是在关键字和存储位置之间建立了对应关系,但是由于冲突的发生,哈希表的查找仍然是一个和关键字比较的过程,不过哈希表平均查找长度比顺序查找要小得多,比二分查找也小。
查找过程中需和给定值进行比较的关键字个数取决于下列三个因素:哈希函数、处理冲突的方法和哈希表的装填因子。
哈希函数的"好坏"首先影响出现冲突的频繁程度,但如果哈希函数是均匀的,则一般不考虑它对平均查找长度的影响。
对同一组关键字,设定相同的哈希函数,但使用不同的冲突处理方法,会得到不同的哈希表,它们的平均查找长度也不同。
一般情况下,处理冲突方法相同的哈希表,其平均查找长度依赖于哈希表的装填因子α。显然,α越小,产生冲突的机会就越大;但α过小,空间的浪费就过多。通过选择一个合适的装填因子α,可以将平均查找长度限定在一个范围内。
总而言之,哈希表“定址”和“解决冲突”之间的权衡决定了哈希表的性能。
7. 哈希表实例
一个哈希表实现的C++实例,在此设计的散列表针对的是关键字为字符串的元素,采用字符串散列函数方法3进行设计散列函数,采用链接方法处理碰撞,然后采用根据装载因子(指定为1,同时将n个元素映射到一个链表上,即n==m时候)进行再散列。采用C++,借助vector和list,设计的hash表框架如下:
template <class T> class HashTable { public: HashTable(int size = 101); int insert(const T& x); int remove(const T& x); int contains(const T& x); void make_empty(); void display()const; private: vector<list<T> > lists; int currentSize;//当前散列表中元素的个数 int hash(const string& key); int myhash(const T& x); void rehash(); };
实现的完整程序如下所示:
#include <iostream> #include <vector> #include <list> #include <string> #include <cstdlib> #include <cmath> #include <algorithm> using namespace std; int nextPrime(const int n); template <class T> class HashTable { public: HashTable(int size = 101); int insert(const T& x); int remove(const T& x); int contains(const T& x); void make_empty(); void display()const; private: vector<list<T> > lists; int currentSize; int hash(const string& key); int myhash(const T& x); void rehash(); }; template <class T> HashTable<T>::HashTable(int size) { lists = vector<list<T> >(size); currentSize = 0; } template <class T> int HashTable<T>::hash(const string& key) { int hashVal = 0; int tableSize = lists.size(); for(int i=0;i<key.length();i++) hashVal = 37*hashVal+key[i]; hashVal %= tableSize; if(hashVal < 0) hashVal += tableSize; return hashVal; } template <class T> int HashTable<T>:: myhash(const T& x) { string key = x.getName(); return hash(key); } template <class T> int HashTable<T>::insert(const T& x) { list<T> &whichlist = lists[myhash(x)]; if(find(whichlist.begin(),whichlist.end(),x) != whichlist.end()) return 0; whichlist.push_back(x); currentSize = currentSize + 1; if(currentSize > lists.size()) rehash(); return 1; } template <class T> int HashTable<T>::remove(const T& x) { typename std::list<T>::iterator iter; list<T> &whichlist = lists[myhash(x)]; iter = find(whichlist.begin(),whichlist.end(),x); if( iter != whichlist.end()) { whichlist.erase(iter); currentSize--; return 1; } return 0; } template <class T> int HashTable<T>::contains(const T& x) { list<T> whichlist; typename std::list<T>::iterator iter; whichlist = lists[myhash(x)]; iter = find(whichlist.begin(),whichlist.end(),x); if( iter != whichlist.end()) return 1; return 0; } template <class T> void HashTable<T>::make_empty() { for(int i=0;i<lists.size();i++) lists[i].clear(); currentSize = 0; return 0; } template <class T> void HashTable<T>::rehash() { vector<list<T> > oldLists = lists; lists.resize(nextPrime(2*lists.size())); for(int i=0;i<lists.size();i++) lists[i].clear(); currentSize = 0; for(int i=0;i<oldLists.size();i++) { typename std::list<T>::iterator iter = oldLists[i].begin(); while(iter != oldLists[i].end()) insert(*iter++); } } template <class T> void HashTable<T>::display()const { for(int i=0;i<lists.size();i++) { cout<<i<<": "; typename std::list<T>::const_iterator iter = lists[i].begin(); while(iter != lists[i].end()) { cout<<*iter<<" "; ++iter; } cout<<endl; } } int nextPrime(const int n) { int ret,i; ret = n; while(1) { int flag = 1; for(i=2;i<sqrt(ret);i++) if(ret % i == 0) { flag = 0; break; } if(flag == 1) break; else { ret = ret +1; continue; } } return ret; } class Employee { public: Employee(){} Employee(const string n,int s=0):name(n),salary(s){ } const string & getName()const { return name; } bool operator == (const Employee &rhs) const { return getName() == rhs.getName(); } bool operator != (const Employee &rhs) const { return !(*this == rhs); } friend ostream& operator <<(ostream& out,const Employee& e) { out<<"("<<e.name<<","<<e.salary<<") "; return out; } private: string name; int salary; }; int main() { Employee e1("Tom",6000); Employee e2("Anker",7000); Employee e3("Jermey",8000); Employee e4("Lucy",7500); HashTable<Employee> emp_table(13); emp_table.insert(e1); emp_table.insert(e2); emp_table.insert(e3); emp_table.insert(e4); cout<<"Hash table is: "<<endl; emp_table.display(); if(emp_table.contains(e4) == 1) cout<<"Tom is exist in hash table"<<endl; if(emp_table.remove(e1) == 1) cout<<"Removing Tom form the hash table successfully"<<endl; if(emp_table.contains(e1) == 1) cout<<"Tom is exist in hash table"<<endl; else cout<<"Tom is not exist in hash table"<<endl; //emp_table.display(); exit(0); }