树
客观世界中许多事物存在层次关系
eg:人类社会家谱
社会组织结构
图书信息管理
分层次组织在管理上具有更高的效率
查找(Searching):给定某个关键字K,从集合R中找出关键字与K相同的记录
静态查找:集合中记录是固定的
没有插入和删除操作,只有查找
动态查找:集合中记录是动态变化的
除查找,还可能发生查找和删除
静态查找
- 顺序查找
typedef struct LNode *List;
struct LNode{
ElementType Element[MAXSIZE];
int Length;
}
int SequentialSearch(List Tb1, ElementType K){
int i;
Tb1->Element[0]=K;//哨兵!这样可以减少判断
for(i=Tb1->Length;Tb1->Element[i]!=K;i--);
return i;
}
- 二分查找 Binary Search O(log(n))
假设n个数据元素的关键字满足有序(k_1<k_2<k_3<...<k_n),并且是连续存放(数组),那么可以进行二分查找。
typedef LNode *List;
struct LNode{
ElementType Element[MAXSIZE];
int Length;
}
int BinarySearch(List PtrL,ElementType k){
int left,right,mid;
left=1;
right=PtrL->Length;
while(left<=right){
mid=(right+left)/2;
if(PtrL->Element[mid]>k) right=mid-1;
if(PtrL->Element[mid]<k) left=mid+1;
else return mid;
}
return NotFound;
}
11个元素的二分查找判定树
判定树上每个结点需要的查找次数刚好为该结点所在的层数,查找成功时查找次数不会超过判定树的深度。n个结点的判定树的深度为logn+1
树定义
树:n个结点构成的有限集合
当n=0时,称为空树
对于任一棵非空树(n>0),它具备一下性质:
(1)树中有一个称为“根”的特殊结点,用r表示
(2)其余结点可分为m个互不相交的有限集(T_1,T_2,...,T_m),其中每个集合本身又是一棵树,称为原来树的“子树(SubTree)”。
子树是不相交的;
除了根结点外,每个结点有且仅有一个父结点;
一棵N个结点的树有N-1条边
基本术语
- 结点的度(Degree):结点的子树的个数
- 树的度:树的所有结点中最大的度数
- 叶结点:度为0的结点
- 父结点: 有子树的结点是其子树的根结点的父结点
- 子结点:
- 兄弟结点:
- 路径和路径长度:
- 祖先结点:
- 子孙结点:
- 结点的层次(level):规定根结点在1曾,其他任一结点的层数是其父结点的层数加一
- 树的深度(Depth):树中所有结点中最大层次是这棵树的深度
树的表示
- 数组表示法:关系表达不清楚
- 多个指针的链表: 比如每个结点3个叉,则3n个指针,而实际只用n-1个,所以浪费了2n+1个指针
- 儿子-兄弟表示法:第一个指针指向其第一个child,第二个指针指向其第一个兄弟
结构是统一的;空间浪费少;
旋转45度可以看成二叉树(知道为什么二叉树重要了吧!)
二叉树的定义
- 二叉树T:一个有穷的结点集合
这个集合可以为空
若不为空,则它是由根结点和称为其左子树(T_L)和右子树(T_R)的两个不相交的二叉树组成
二叉树有五种基本形态
二叉树的子树有左右顺序之分
-
特殊的二叉树
(1)斜二叉树
(2)完美二叉树/满二叉树
(3)完全二叉树:有n个结点的二叉树,对树中结点按从上至下、从左到右顺序进行编号,编号为i结点与满二叉树中变好为i结点在二叉树中位置相同 -
二叉树几个重要性质
(1)第i层最大结点数为:(2^{i-1},i>=1)
(2)深度为k的二叉树最大结点数为:(2^k-1,k>=1)
(3)对任何非空二叉树T,若(n_0)表示叶结点的个数,(n_2)是度为2的非叶结点个数,那么两者满足关系(n_0=n_2+1)
- ADT二叉树
类型名称:二叉树
数据对象集:一个有穷的结点集合
若不为空,则由根结点和其左右二叉子树组成
操作集:
1. Booloen isEmpty(BinTree BT):判断BT是否为空
2. void Traversal(BinTree BT):遍历,按某顺序访问每个结点
3. BinTree CreatBinTree():创建一个二叉树
常见的遍历方法:
(1)先序:根、左、右
(2)中序:左、根、右
(3)后序:左、右、根
(4)层次遍历
二叉树的存储结构
- 顺序存储结构
完全二叉树:按从上至下、从左至右顺序存储n个结点的完全二叉树的结点父子关系
非根结点的父结点:i/2取下界
结点的左孩子:2i
结点的右孩子:2i+1
一般二叉树也可以用这种结构,但会造成空间浪费(补充成一个完全二叉树)
- 链式存储
typedef struct TreeNode *BinTree;
typedef BinTree Position;
struct TreeNode{
ElementType Data;
BinTree Left;
BinTree Right;
}
二叉树的遍历
- 先序遍历
(1)先访问根结点
(2)先序遍历其左子树
(3)先序遍历其右子树
void PreOrderTraversal(BinTree BT){
if(BT){
printf("%d",BT->Data);
PreOrderTraversal(BT->Left);
PreOrderTraversal(BT->Right);
}
}
- 中序遍历
(1)中序遍历其左子树
(2)访问根结点
(3)中序遍历其右子树
void InOrderTraversal(BinTree BT){
if(BT){
InOrderTraversal(BT->Left);
printf("%d",BT->Data);
InOrderTraversal(BT->Right);
}
}
- 后序遍历
(1)后序遍历其左子树
(2)后序遍历其右子树
(3)访问根结点
void PostOrderTraversal(BinTree BT){
if(BT){
PostOrderTraversal(BT->Left);
PostOrderTraversal(BT->Right);
printf("%d",BT->Data);
}
}
先序、中序和后序遍历过程,遍历过程中经过结点的路线一样,只是访问各结点的时机不同(妙啊!)
- 非递归遍历
中序遍历非递归遍历算法
非递归算法实现的基本思路:使用堆栈
遇到一个结点,就把它压栈,病区遍历它的左子树;
当左子树遍历结束后,从栈顶弹出这个结点并访问它;
然后按其右指针再去中序遍历该结点的右子树
void InOrderTraversal(BinTree BT){
BinTree T=BT;
Stack S=CreatStack(MaxSize);
while(T||!IsEmpty(S)){//最妙的就是这个循环,结束的条件就是树访问完并且堆栈空了
while(T){
Push(S,T);
T=T->Left;
}
if(!IsEmpty(S)){
T=Pop(S);
printf("%5d",T->Data);
T=T->Right;
}
}
反思:
这一段,太妙了!怎么能想出这一段呢?首先,把遍历路径的感觉找到。遍历的路径都是先一直向左,向左的过程中不断把元素压到栈中,向左到头以后,推出栈内的元素并访问。然后在其右指针中遍历该结点的右子树
void PreOrderTraversal(BinTree BT){
BinTree T=BT;
Stack S=CreatStack(MaxSize);
while(T||!IsEmpty(S)){//最妙的就是这个循环,结束的条件就是树访问完并且堆栈空了
while(T){
Push(S,T);
printf("%5d",T->Data);
T=T->Left;
}
if(!IsEmpty(S)){
T=Pop(S);
T=T->Right;
}
}
void PostOrderTraversal(BinTree BT){
BinTree T=BT;
Stack S=CreatStack(MaxSize);
while(T||!IsEmpty(S)){//最妙的就是这个循环,结束的条件就是树访问完并且堆栈空了
while(T){
Push(S,T);
T=T->Left;
}
if(!IsEmpty(S)){
T=Pop(S);
T=T->Right;
}
printf("%5d",T->Data);//还得再想想
}
层序遍历
二叉树遍历的核心问题:二维结构的线性化
从结点访问其左、右儿子结点
访问左儿子后,右儿子结点怎么办:需要一个存储结构保存暂时不访问的结点;存储结构:堆栈,队列
- 队列实现
遍历从根结点开始,首先将根结点入队,然后开始执行循环:结点出队、访问该结点、其左右儿子入队
层序遍历过程:先根结点入队,然后:
(1)从队列中取出一个元素;
(2)访问该元素所指的结点;
(3)若该元素所指结点的左、右孩子结点非空,则将其左、右孩子的指针顺序入队。
void LevelOrdertraversal(BinTree BT){
Queue Q; BinTree T;
if(!BT) return;
Q=CreatQueue(MaxSize);
AddQ(Q,BT);
while(!IsEmpty(Q)){
T=Delete(Q);
printf("%d",T->Data);
if(T->Left) AddQ(Q,T->Left);
if(T->Right) AddQ(Q,T->Right);
}
}
反思:
这个步骤基本就是顺着把上面的描述写了出来。值得注意的是AddQ()这个函数,推入的是左右两个孩子结点的地址。而返回的时候返回的也是个地址。那么这个Queue里的ElementType就可以直接整成TNode的形式(因为这就是入队和出队的元素啊!)
应用:输出二叉树中的叶子结点
void PreOrderPrintLeaves(BinTree BT){
if(BT){
if(!BT->Left&&!BT->Right) printf("%d",BT->Data);
PreOrderPrintLeaves(BT->Left);
PreOrderPrintLeaves(BT->Right);
}
}
应用:求二叉树的高度
int PostOrderGetHeight(BinTree BT){
int HL,HR,MaxH;
if(BT){
HL=PostordergetHeight(BT->Left);
HR=PostOrderGetHeight(BT->Right);
MaxH=(HL>HR)?HL:HR;
return (MaxH+1);
}
else return 0;
}
应用:二元运算表达式树及其遍历
先序遍历得到前缀表达式
中序遍历得到中缀表达式(不一定是准的,输出左子树的时候先输出括号)
后序遍历得到后缀表达式
由两种遍历序列确定二叉树,必须要有中序遍历才行!
eg:
先序序列:a b c d e f g h i j
中序序列:c b e d a h g i j f
树的同构
- 问题:给定两棵树(T_1)和(T_2)。如果(T_1)可以通过若干次左右孩子互换就变成(T_2),则我们称两棵树是“同构的”
输入样例:
8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -
-
求解思路
二叉树的表示
建二叉树
同构判别 -
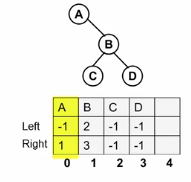
二叉树表示
看成完全二叉树,缺少的结点空出来
本题使用结构数组表示二叉树:静态链表(物理存储是数组,思想上是链表)
#define MaxTree 10
#define Tree int
#define ElementType char
#define Null -1
struct TreeNode{
ElementType Element;
Tree Left;
Tree Right;
}T1[MaxTree],T2[MaxTree];
- 程序框架搭建
int main(){
建二叉树1
建二叉树2
判别是否是同构并输出
return 0;
}
需要设计的函数:
读数据建二叉树
二叉树同构判别
int main(){
Tree R1,R2;
R1=BuildTree(T1);
R2=BuildTree(T2);
if(Isomorphic(R1,R2)) printf("Yes
");
else printf("No
");
return 0;
}
完整程序:
#include <iostream>
using namespace std;
#define ElementType char
#define Tree int
#define MaxSize 20
#define Null -1;
struct TreeNode{//本题使用结构数组的思路来做,结构数组在存储上是数组,逻辑上是链表
ElementType Element;
Tree Left;
Tree Right;
}T1[MaxSize],T2[MaxSize];
//实际上树是存储在T1和T2里面的,而使用的时候直接用R1,R2即可。相当于编程的人知道R1对应T1,R2对应T2
Tree BuildTree(struct TreeNode T[]){
int N=0;
Tree Root=Null;
char cl,cr;
scanf("%d",&N);
int check[N];//使用一个数组,看看哪些结点被指向了,没有被指向的那个,就是我们的root,嘿嘿嘿
if(!N){
for(int i=0;i<N;i++) check[i]=0;
for(int i=0;i<N;i++){
scanf("%c %c %c",&T[i].Element,&cl,&cr);
//这里采用char类型输入的原因:因为输入的时候有'-',就算没有'-',这样处理也是没有问题
if(cl!='-'){
T[i].Left=cl-'0';
check[T[i].Left]=1;
}
else T[i].Left=Null;
if(cr!='-'){
T[i].Right=cr-'0';
check[T[i].Right]=1;
}
else T[i].Right=Null;
}
int i;
for(i=0;i<N;i++)
if(!check[i]) break;
Root = i;
}
return Root;
};
int Isomorphic(Tree R1,Tree R2){
if((R1==-1)&&(R2==-1))
return 1;
if(((R1==-1)&&(R2!=-1))||((R1!=-1)&&(R2==-1)))
return 0;
if(T1[R1].Element!=T2[R2].Element)
return 0;
if((T1[R1].Left==-1)&&(T2[R2].Left==-1))
return Isomorphic(T1[R1].Right, T2[R2].Right);
if(((T1[R1].Left!=-1)&&T2[R2].Left!=-1)&&((T1[T1[R1].Left].Element)==(T2[T2[R2].Left].Element)))
return (Isomorphic(T1[R1].Left, T2[R2].Left)&&Isomorphic(T1[R1].Right, T2[R2].Right));
else
return(Isomorphic(T1[R1].Left, T2[R2].Right)&&Isomorphic(T1[R1].Right, T2[R2].Left));
}
int main(int argc, const char * argv[]) {
Tree R1,R2;
R1=BuildTree(T1);
R2=BuildTree(T2);
if(Isomorphic(R1,R2)) printf("Yes
");
else printf("No
");
return 0;
}