哈夫曼编码测试

1.哈夫曼树介绍

在计算机数据处理中，霍夫曼编码使用变长编码表对源符号（如文件中的一个字母）进行编码，其中变长编码表是通过一种评估来源符号出现机率的方法得到的，出现机率高的字母使用较短的编码，反之出现机率低的则使用较长的编码，这便使编码之后的字符串的平均长度、期望值降低，从而达到无损压缩数据的目的。

例如，在英文中，e的出现机率最高，而z的出现概率则最低。当利用霍夫曼编码对一篇英文进行压缩时，e极有可能用一个比特来表示，而z则可能花去25个比特（不是26）。用普通的表示方法时，每个英文字母均占用一个字节（byte），即8个比特。二者相比，e使用了一般编码的1/8的长度，z则使用了3倍多。倘若我们能实现对于英文中各个字母出现概率的较准确的估算，就可以大幅度提高无损压缩的比例。

霍夫曼树又称最优二叉树，是一种带权路径长度最短的二叉树。所谓树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）。树的路径长度是从树根到每一结点的路径长度之和，记为WPL=（W1L1+W2L2+W3L3+...+WnLn），N个权值Wi（i=1,2,...n）构成一棵有N个叶结点的二叉树，相应的叶结点的路径长度为Li（i=1,2,...n）。可以证明霍夫曼树的WPL是最小的。

演算过程
进行霍夫曼编码前，我们先创建一个霍夫曼树。

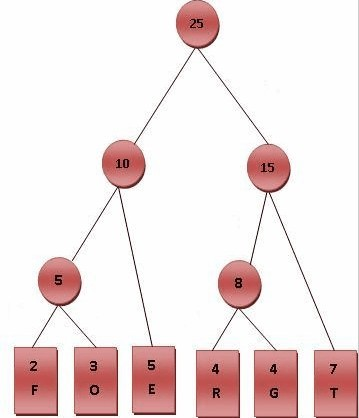
⒈将每个英文字母依照出现频率由小排到大，最小在左。

⒉每个字母都代表一个终端节点（叶节点），比较F.O.R.G.E.T五个字母中每个字母的出现频率，将最小的两个字母频率相加合成一个新的节点。如Fig.2所示，发现F与O的频率最小，故相加2+3=5。

⒊比较5.R.G.E.T，发现R与G的频率最小，故相加4+4=8。

⒋比较5.8.E.T，发现5与E的频率最小，故相加5+5=10。

⒌比较8.10.T，发现8与T的频率最小，故相加8+7=15。

⒍最后剩10.15，没有可以比较的对象，相加10+15=25。

进行编码

1.给霍夫曼树的所有左链结'0'与
霍夫曼树
霍夫曼树
右链结'1'。

2.从树根至树叶依序记录所有字母的编码

2.实验内容

设有字符集：S={a,b,c,d,e，f,g,h,i,j,k,l,m,n.o.p.q,r,s,t,u,v,w,x,y,z}。
给定一个包含26个英文字母的文件，统计每个字符出现的概率，根据计算的概率构造一颗哈夫曼树。
并完成对英文文件的编码和解码。
要求：
（1）准备一个包含26个英文字母的英文文件（可以不包含标点符号等），统计各个字符的概率
（2）构造哈夫曼树
（3）对英文文件进行编码，输出一个编码后的文件
（4）对编码文件进行解码，输出一个解码后的文件
（5）撰写博客记录实验的设计和实现过程，并将源代码传到码云
（6）把实验结果截图上传到云班课
满分：6分。
酌情打分。

3. 实验过程及结果

HuffmanNode类 实现哈夫曼树的结点

public class HuffmanNode   {
    private int weight;//权值
    private int parent;
    private int leftChild;
    private int rightChild;

    public HuffmanNode(int weight,int parent,int leftChild,int rightChild){
        this.weight=weight;
        this.parent=parent;
        this.leftChild=leftChild;
        this.rightChild=rightChild;
    }

    void setWeight(int weight){
        this.weight=weight;
    }

    void setParent(int parent){
        this.parent=parent;
    }

    void setLeftChild(int leftChild){
        this.leftChild=leftChild;
    }

    void setRightChild(int rightChild){
        this.rightChild=rightChild;
    }

    int getWeight(){
        return weight;
    }

    int getParent(){
        return parent;
    }

    int getLeftChild(){
        return leftChild;
    }

    int getRightChild(){
        return rightChild;
    }
}

HuffmanCode 类 记录所用的字符及对应的编码

public class HuffmanCode {
    private String character;
    private String code;
    HuffmanCode(String character,String code){
        this.character=character;
        this.code=code;
    }
    HuffmanCode(String code){
        this.code= code;
    }

    void setCharacter(String character){
        this.character=character;
    }

    void setCode(String code){
        this.code=code;
    }

    String getCharacter(){
        return character;
    }

    String getCode(){
        return code;
    }
}

HuffmanTree类，实现哈夫曼树以及每个符号获得对应的前缀码

public class HuffmanTree {
    //初始化一个huffuman树
    public static void initHuffmanTree(HuffmanNode[] huffmanTree,int m){
        for(int i=0;i<m;i++){
            huffmanTree[i] = new HuffmanNode(0,-1,-1,-1);
        }
    }

    //初始化一个huffmanCode
    public static void initHuffmanCode(HuffmanCode[] huffmanCode,int n){
        for(int i=0;i<n;i++){
            huffmanCode[i]=new HuffmanCode("","");
        }
    }

    //获取huffmanCode的符号
    public static void getHuffmanCode(HuffmanCode[] huffmanCode , int n,char[] chars){
        for(int i=0;i<n;i++){
            String temp = ""+chars[i];
            huffmanCode[i] = new HuffmanCode(temp,"");
        }
    }

    //获取huffman树节点频数
    public static void getHuffmanWeight(HuffmanNode[] huffmanTree , int n,int[] ints){
        for(int i=0;i<n;i++){
            int temp = ints[i];
            huffmanTree[i] = new HuffmanNode(temp,-1,-1,-1);
        }
    }

    //从n个结点中选取最小的两个结点
    public static int[] selectMin(HuffmanNode[] huffmanTree ,int n)
    {
        int min[] = new int[2];
        class TempNode
        {
            int newWeight;//存储权
            int place;//存储该结点所在的位置

            TempNode(int newWeight,int place){
                this.newWeight=newWeight;
                this.place=place;
            }

            void setNewWeight(int newWeight){
                this.newWeight=newWeight;
            }

            void setPlace(int place){
                this.place=place;
            }

            int getNewWeight(){
                return newWeight;
            }

            int getPlace(){
                return place;
            }
        }

        TempNode[] tempTree=new TempNode[n];

        //将huffmanTree中没有双亲的结点存储到tempTree中
        int i=0,j=0;
        for(i=0;i<n;i++)
        {
            if(huffmanTree[i].getParent()==-1&& huffmanTree[i].getWeight()!=0)
            {
                tempTree[j]= new TempNode(huffmanTree[i].getWeight(),i);
                j++;
            }
        }

        int m1,m2;
        m1=m2=0;
        for(i=0;i<j;i++)
        {
            if(tempTree[i].getNewWeight()<tempTree[m1].getNewWeight())//此处不让取到相等，是因为结点中有相同权值的时候，m1取最前的
                m1=i;
        }
        for(i=0;i<j;i++)
        {
            if(m1==m2)
                m2++;//当m1在第一个位置的时候，m2向后移一位
            if(tempTree[i].getNewWeight()<=tempTree[m2].getNewWeight()&& i!=m1)//此处取到相等，是让在结点中有相同的权值的时候，

                //m2取最后的那个。
                m2=i;
        }

        min[0]=tempTree[m1].getPlace();
        min[1]=tempTree[m2].getPlace();
        return min;
    }

    //创建huffmanTree
    public static void createHaffmanTree(HuffmanNode[] huffmanTree,int n){
        if(n<=1)
            System.out.println("Parameter Error!");
        int m = 2*n-1;
        //initHuffmanTree(huffmanTree,m);

        for(int i=n;i<m;i++)
        {
            int[] min=selectMin(huffmanTree,i);
            int min1=min[0];
            int min2=min[1];
            huffmanTree[min1].setParent(i);
            huffmanTree[min2].setParent(i);
            huffmanTree[i].setLeftChild(min1);
            huffmanTree[i].setRightChild(min2);
            huffmanTree[i].setWeight(huffmanTree[min1].getWeight()+ huffmanTree[min2].getWeight());
        }
    }

    //创建huffmanCode
    public static void createHaffmanCode(HuffmanNode[] huffmanTree,HuffmanCode[] huffmanCode,int n){
        char[] code = new char[26];
        int start;
        int c;
        int parent;
        int temp;

        code[n-1]='0';
        for(int i=0;i<n;i++)
        {
            StringBuffer stringBuffer = new StringBuffer();
            start=n-1;
            c=i;
            while( (parent=huffmanTree[c].getParent()) >=0 )
            {
                start--;
                code[start]=((huffmanTree[parent].getLeftChild()==c)?'0':'1');
                c=parent;

            }
            for(;start<n-1;start++){
                stringBuffer.append(code[start]);
            }
            huffmanCode[i].setCode(stringBuffer.toString());
        }
    }

HuffmanTest类 读取相应的文件并做出加密解密操作

import java.io.*;

import static week15.HuffmanTree.*;

public class HuffmanTest {
    private char[] chars = new char[]{'a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s'
            ,'t','u','v','w','x','y','z'};
    private  int[] number = new int[]{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0};

    public String txtString(File file){
        StringBuilder result = new StringBuilder();
        try{
            BufferedReader br = new BufferedReader(new FileReader(file));//构造一个BufferedReader类来读取文件
            String s = null;
            while((s = br.readLine())!=null){//使用readLine方法，一次读一行
                result.append(System.lineSeparator()+s);
                num(s);
            }
            br.close();
        }catch(Exception e){
            e.printStackTrace();
        }
        return result.toString();
    }

    public void num(String string){
        for(int i = 0;i<26;i++){
            int temp = 0;
            for(int j = 0;j<string.length();j++){
                if(string.charAt(j) == chars[i])
                    temp++;
            }
            number[i] += temp;
        }
    }

    public int[] getNumber(){
        return number;
    }

    public char[] getChars(){
        return chars;
    }

    public static void main(String[] args){
        File file = new File("D:\","inputhuffman.txt");
        HuffmanTest huffmanTest= new HuffmanTest();
        String temp = huffmanTest.txtString(file);
        int[] num = huffmanTest.getNumber();

        char[] chars = huffmanTest.getChars();

        int n;
        int m;
        n = 26;
        m=2*n-1;
        HuffmanNode[] huffmanTree = new HuffmanNode[m];
        HuffmanCode[] huffmanCode = new HuffmanCode[n];

        //初始化huffmanTree,huffmanCode
        initHuffmanTree(huffmanTree,m);
        initHuffmanCode(huffmanCode,n);

        //获取huffmanCode的符号
            getHuffmanCode(huffmanCode,n,chars);
        //获取huffmanTree的频数
            getHuffmanWeight(huffmanTree,n,num);

        //创建huffmanTree
        createHaffmanTree(huffmanTree,n);
        //创建huffmanCode
        createHaffmanCode(huffmanTree,huffmanCode,n);

        //输出huffmanCode编码
        ouputHaffmanCode(huffmanCode,n);

        String result = "";
        for(int i = 0;i<temp.length();i++){
            for(int j = 0;j<huffmanCode.length;j++){
                if(temp.charAt(i) == huffmanCode[j].getCharacter().charAt(0))
                    result +=huffmanCode[j].getCode();
            }
        }
        System.out.println("加密");
        System.out.println(result);
        System.out.println("解密");
}

3. 实验过程中遇到的问题和解决过程

问题1：只输出了两个数的编码

问题1解决方案：
错误地将26个字符数删成两个 于是其他地方输入多少个也没用

改正之后就没问题了

其他（感悟、思考等）

参考资料

• 《Java软件结构与数据结构教程（第四版）》