0、小叙闲言
第一次学习MATLAB,主要是为了今后学习做图像处理的。现阶段主要是准备学一些基础的编程知识,对MATLAB有一定的了解和基础以后再学习图像处理,磨刀不误砍柴工!
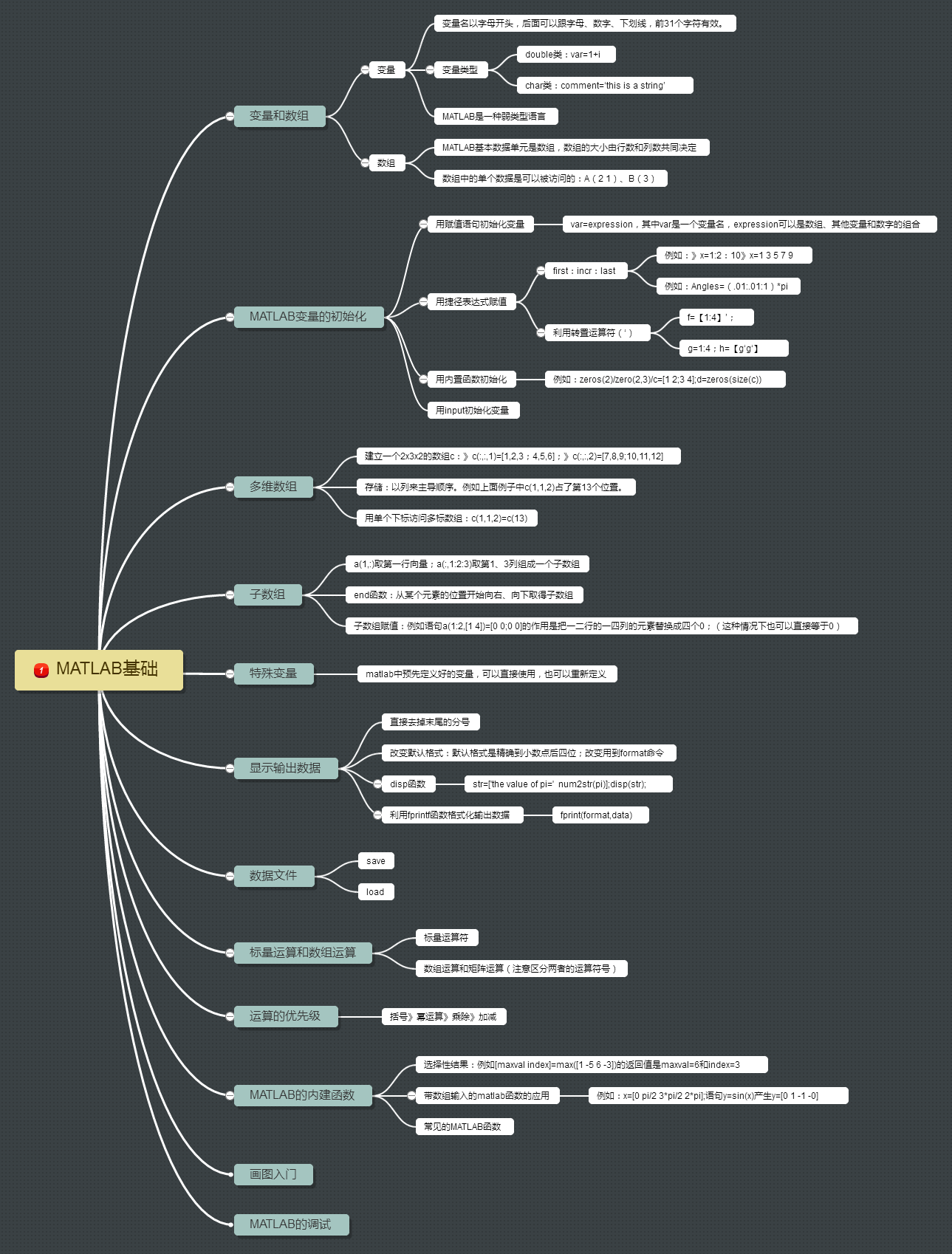
1、思维导图
为了在学习思路上清晰明了,学习运用软件做了这样的思维导图,可以对本章知识结构一目了然,主要是为了以后翻看起来可以很快回忆起看过学过的内容。
2、书中典例
例1:用关键字input初始化变量
>> in1=input('enter data:')
enter data:1.23
输入命令以后,回车,用户自行输入相应的初始化值
例2:子数组
>> arr2=[1 2 3;-2 -3 -4;3 4 5];
>> arr2(:,1:2:3)
ans =
1 3
-2 -4
3 5
只是一个简单的子数组输出,这里体现出“(:,1:2:3)”的意思是所有行、第一列和第三列组成的数组。
例3:改变默认格式
>> x=32.78578; >> format hex; >> x x = 404064947064ecea
此处显示输出数据时采用了format来改变默认格式。MATLAB中数据的默认格式是精确到小数点后四位。
例4:disp函数
>> str=['the value of pi=' num2str(pi)]; >> disp(str) the value of pi=3.1416
disp函数使用时需要一个数组参数,本例中当然就是str了,将使值显示在命令窗口。如果数组中是字符,该字符串将会显示出来,本例中便是这样的。另外例子中包含了一个num2str(将一个数转化为字符串),这个函数常常和disp联合在一起使用。类似的函数还有int2str(将一个整数转化为字符串)。
例5:使用fprintf函数格式化输出数据
>> fprintf('the value of pi is %6.2f
',pi)
the value of pi is 3.14
>>
转义序号%6.2代表在本函数中第一个数据项将占据6个字符宽度,小数点后有两位小数。另外类似于c语言," "代表回车另起一行。另外需要注意的是fprintf函数只能显示复数的实部,所以会产生错误。例如下面的例子:
>> fprintf('the value of pi is %6.2f
',2+2*i)
the value of pi is 2.00
>>
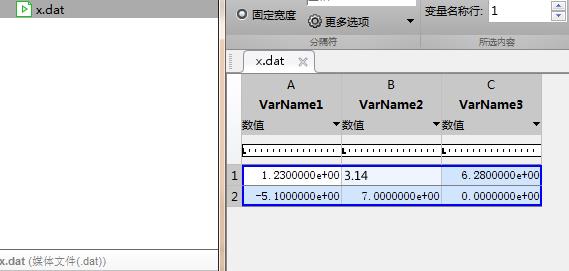
例6:save命令和load命令
save命令用于保存当前matlab工作区的数据到一个硬盘文件。
>> x=[1.23 3.14 6.28;-5.1 7.00 0]; >> save x.dat x -ascii
上面的代码得到一个文件x.dat,如下:
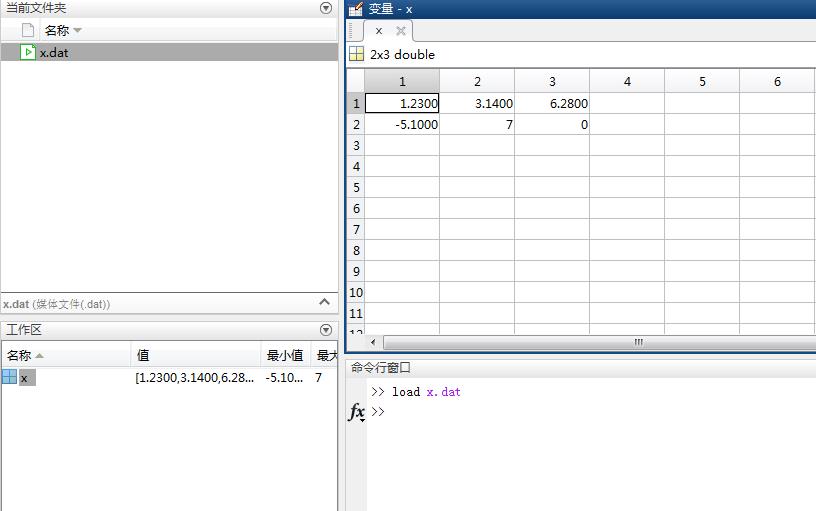
load命令和save命令正好相反,从硬盘文件加载数据到工作区,函数使用格式为:load filename,如下:
例7:MATLAB作图之画图入门
首先生成两个向量,分别由x、y表示,然后可以借助plot函数,简单代码如下:
>> x=0:1:10; >> y=x.^2-10*x+15; >> plot(x,y)
结果如下:
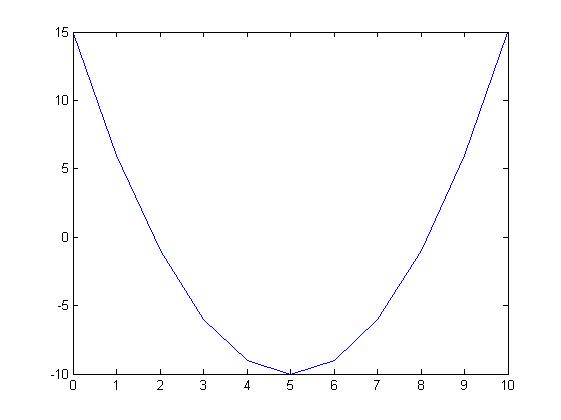
可以看到上图中只是一个简单的图形,现在在图像上加上标题以及x、y轴的信息,可以借助title、xlabel、ylabel等函数。如下:
>> x=0:1:10;
>> y=x.^2-10*x+15;
>> plot(x,y);
>> title('Plot of y=x.^2-10*x+15');
>> xlabel('x');
>> ylabel('y');
>> grid on
结果如下:
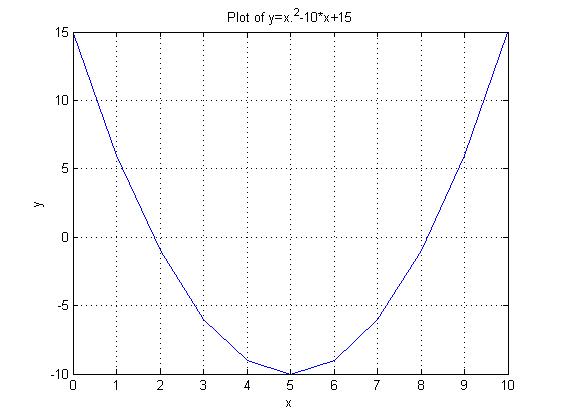
代码中的grid on表示生成网格线。
例8:MATLAB作图之联合作图
联合做图其实很简单,这里不做很多解释了,代码如下:
x=0:pi/100:2*pi; y1=sin(2*x); y2=2*cos(2*x); plot(x,y1,x,y2);
结果如下:
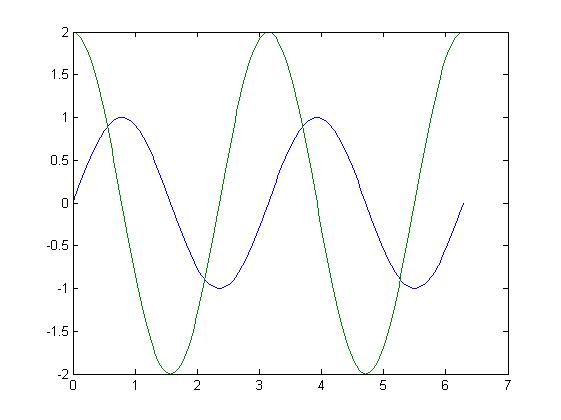
例9:MATLAB作图之线色、线型、符号、图例
具体符号见下表:
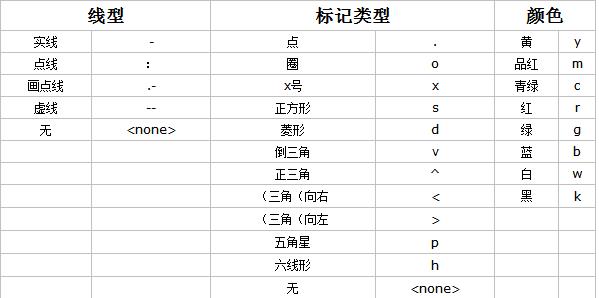
书中的例子是这样的:
x = 0:1:10; y = x.^2 -10.*x +15; plot(x,y,'r--',x,y,'bo');
生成的图像如下
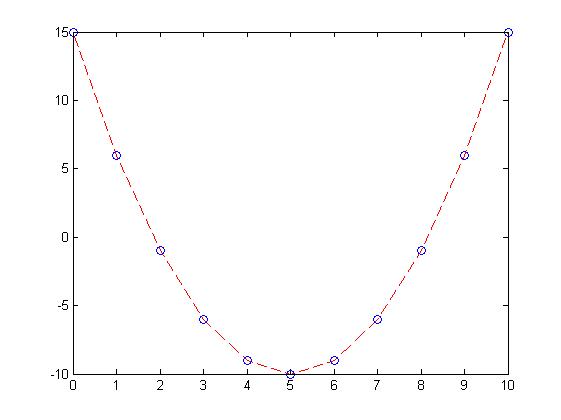
结合代码和图像来看:r--代表红色虚线;bo代表蓝色的圈。
另外,还可以使用legend来制作图例,基本格式如下:
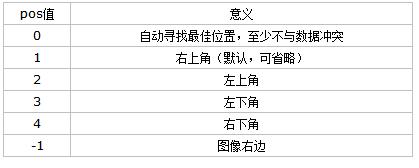
legend(‘string1’,‘string2’,…,pos),其中string1,string2等是轨迹名,pos主要用来表示图例的位置。pos值意义具体如下:
书中的例子如下:
x=0:pi/100:2*pi;
y1=sin(2*x);
y2=2*cos(2*x);
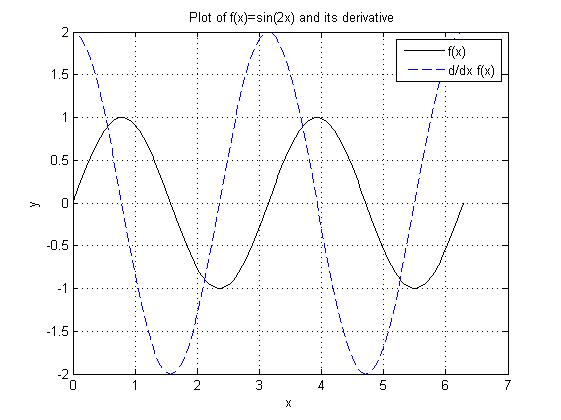
plot(x,y1,'k-',x,y2,'b--');
title(' Plot of f(x)=sin(2x) and its derivative');
xlabel('x');
ylabel('y');
legend('f(x)','d/dx f(x)')
grid on;
结果如下:
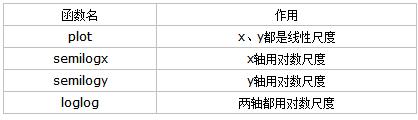
例10:MATLAB作图之对数尺度
matlab中对于坐标轴的取对数函数如下表:
这里一次运用四个函数进行处理,图像如下:
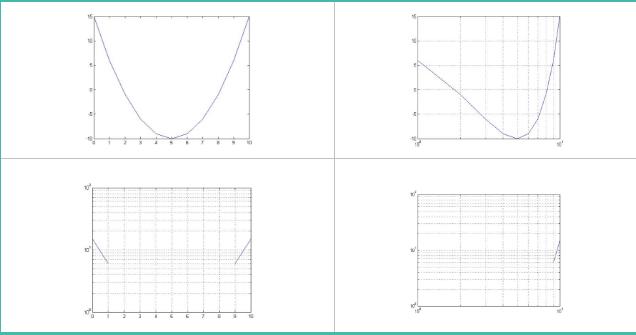
后两幅图由于负数的省略,只出现了一部分,但是从网格的疏密程度依然可以看出对数坐标对图像的影响。
3、总结
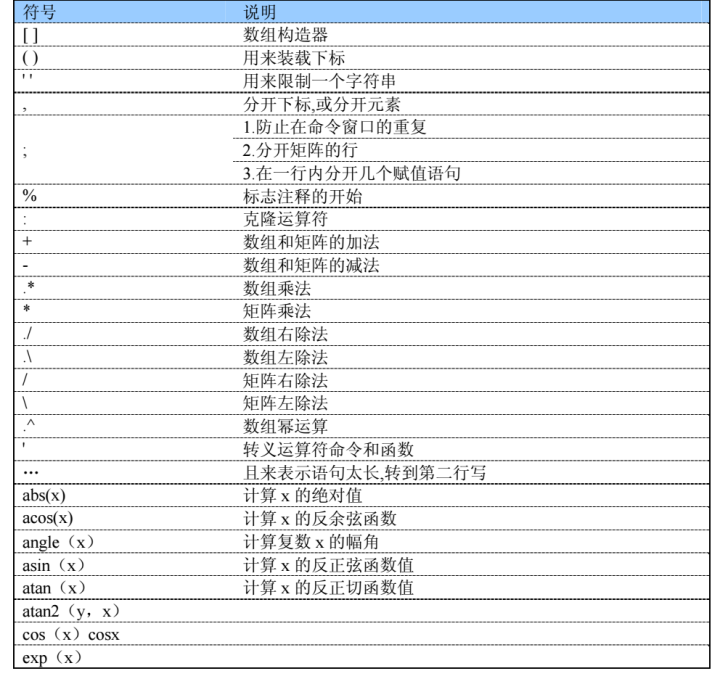
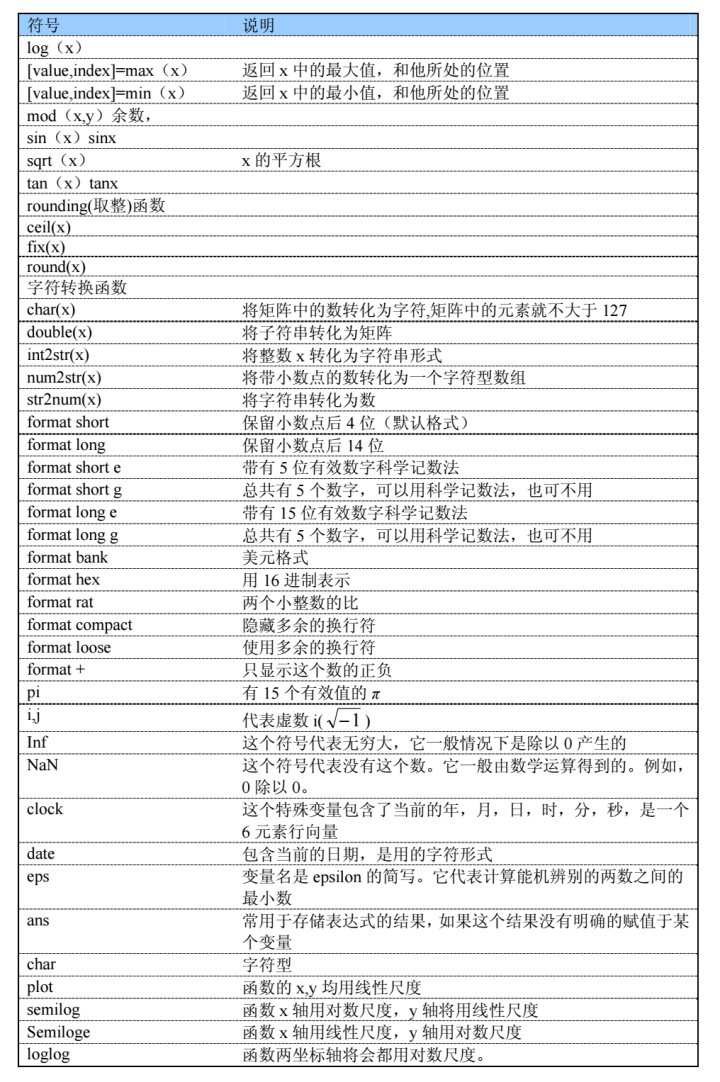
书中出现了很多的符号和函数,总结如下表,方便学习运用:
4、感悟
通过学习基础的编程知识,对比之前学过的c语言,matlab的编程是针对于数组的,所以肯定有些不一样的,对于这样的编程结构一时还适应不过来,但是觉得只要多编写一些程序,还是可以很快适应的,天道酬勤。另外,书中在最后给了一些实际问题中的例子,我看了一下,不难理解,这里就不再赘述了。